Next: Ritzova metoda
Up: Rubni problem
Previous: Rubni problem
Sadržaj
Indeks
Metoda konačnih diferencija
Neka je dan rubni problem
Podijelimo segment
![$ [0,\ell{}]$](img1466.png) na
na 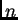 jednakih podsegmenata.
Točke
jednakih podsegmenata.
Točke
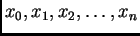 se zovu čvorovi. Točke
se zovu čvorovi. Točke
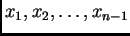 se zovu unutrašnji čvorovi, a
se zovu unutrašnji čvorovi, a
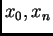 se zovu rubni čvorovi.
Svaki segment ima duljinu
se zovu rubni čvorovi.
Svaki segment ima duljinu
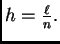 Broj
Broj 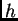 se zove
korak. On se izabire malen, da točnost bude veća, ali sa
smanjivanjem koraka se javljaju drugi nepoželjni efekti, pa u odabiru
koraka treba biti oprezan. Ideja metode se sastoji u tome da se u
svakom čvoru diferencijalna jednadžba zamijeni odgovarajućom
algebarskom jednadžbom i zatim riješi tako dobiveni sustav
algebarskih jednadžbi. U tu svrhu treba derivacije zamijeniti
odgovarajućim algebarskim aproksimacijama. Rješenje koje tako
dobijemo predstavlja približne vrijednosti rješenja u
čvorovima.
se zove
korak. On se izabire malen, da točnost bude veća, ali sa
smanjivanjem koraka se javljaju drugi nepoželjni efekti, pa u odabiru
koraka treba biti oprezan. Ideja metode se sastoji u tome da se u
svakom čvoru diferencijalna jednadžba zamijeni odgovarajućom
algebarskom jednadžbom i zatim riješi tako dobiveni sustav
algebarskih jednadžbi. U tu svrhu treba derivacije zamijeniti
odgovarajućim algebarskim aproksimacijama. Rješenje koje tako
dobijemo predstavlja približne vrijednosti rješenja u
čvorovima.
Uočimo jedan unutrašnji čvor 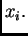 Koristit ćemo sljedeće oznake
Koristit ćemo sljedeće oznake
Na isti način kao u 3.5.1 imamo
Odatle
Ova aproksimacija derivacije se zove aproksimacija s
desna.
Umjesto aproksimacije s desna ponekad se koriste aproksimacija s
lijeva ili centralna aproksimacija. Polazeći od formule
(3.24), u kojoj zamjenimo 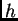 s
s 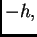
dobivamo, zanemarivanjem člana s 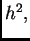 aproksimaciju s lijeva
Centralnu aproksimaciju dobivamo, ako Taylorove formule
za
aproksimaciju s lijeva
Centralnu aproksimaciju dobivamo, ako Taylorove formule
za 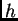 i
i 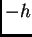 oduzmemo i podijelimo s
oduzmemo i podijelimo s 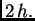 Tada imamo
pa ako zanemarimo član s
Tada imamo
pa ako zanemarimo član s 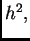 dobivamo
Za aproksimaciju druge derivacije, uzimamo
Zbrojimo ove jednakosti
Podijelimo s
dobivamo
Za aproksimaciju druge derivacije, uzimamo
Zbrojimo ove jednakosti
Podijelimo s 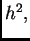 i izračunamo
i izračunamo 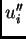 Zanemarimo zadnji član s faktorom
Zanemarimo zadnji član s faktorom 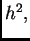 i dobivamo
i dobivamo
U čvoru 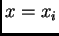 diferencijalna jednadžba iz rubnog problema glasi
diferencijalna jednadžba iz rubnog problema glasi
Zamijenimo li drugu derivaciju s njezinom aproksimacijom, dobijemo
algebarsku jednadžbu za 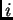 -ti čvor
Pomnožimo jednadžbu s
-ti čvor
Pomnožimo jednadžbu s 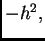 pa imamo
U rubnim čvorovima imamo zadan rubni uvjet. Tako je na lijevom rubu
pa imamo
U rubnim čvorovima imamo zadan rubni uvjet. Tako je na lijevom rubu
Na taj način smo dobili sustav od 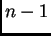 -ne linearne algebarske
jednadžbe. Rubni uvjeti imaju utjecaja samo na prvu jednadžbu
-ne linearne algebarske
jednadžbe. Rubni uvjeti imaju utjecaja samo na prvu jednadžbu
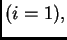 koja postaje, zbog (3.25),
i na zadnju jednadžbu
koja postaje, zbog (3.25),
i na zadnju jednadžbu 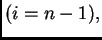 koja, zbog (3.27),
postaje
Sustav možemo zapisati u matričnom obliku. Ako uzmemo
prirodan poredak jednadžbi počevši od čvora
koja, zbog (3.27),
postaje
Sustav možemo zapisati u matričnom obliku. Ako uzmemo
prirodan poredak jednadžbi počevši od čvora 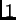 preko
preko 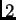 sve do
sve do
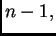 imamo vektor nepoznanica
matricu sustava
i vektor desne strane
Tada sustav možemo zapisati matrično
imamo vektor nepoznanica
matricu sustava
i vektor desne strane
Tada sustav možemo zapisati matrično
Za kvadratnu matricu
![$ A=[a_{ij}]$](img37.png) kažemo da je
striktno dijagonalno dominantna ako je
kažemo da je
striktno dijagonalno dominantna ako je
Može se pokazati da iz striktne dijagonalne dominantnosti matrice 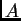 slijedi njezina regularnost. Ako je
slijedi njezina regularnost. Ako je
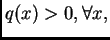 onda je
matrica
onda je
matrica 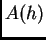 striktno dijagonalno dominantna, pa je regularna. Prema
tome postoji jedinstveno rješenje.
striktno dijagonalno dominantna, pa je regularna. Prema
tome postoji jedinstveno rješenje.
Primjer 3.19
Riješiti metodom konačnih diferencija sljedeći rubni problem
Rješenje. Podijelimo segment ![$ [0,1]$](img3091.png) na deset jednakih dijelova, tako da
je korak
na deset jednakih dijelova, tako da
je korak 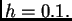 Čvorovi su
Čvorovi su
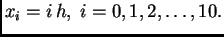 Stavimo
Stavimo
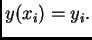 Za prvu derivaciju upotrebimo desnu
aproksimaciju, osim na desnom rubu, gdje uzmemo lijevu. U svakom
unutrašnjem čvoru zamijenimo derivacije odgovarajućim
aproksimacijama. Dobivamo sustav jednadžbi
Za prvu derivaciju upotrebimo desnu
aproksimaciju, osim na desnom rubu, gdje uzmemo lijevu. U svakom
unutrašnjem čvoru zamijenimo derivacije odgovarajućim
aproksimacijama. Dobivamo sustav jednadžbi
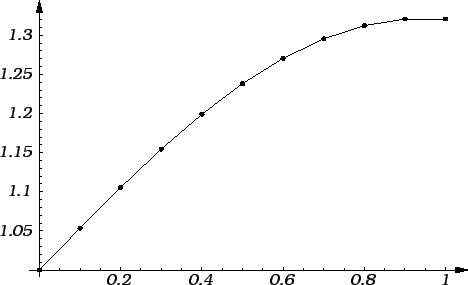
čije rješenje je
Točke rješenja na sljedećoj slici spojene su ravnim linijama.





Next: Ritzova metoda
Up: Rubni problem
Previous: Rubni problem
Sadržaj
Indeks
2001-10-26
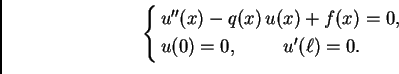
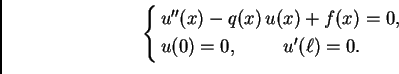
![]() Koristit ćemo sljedeće oznake
Koristit ćemo sljedeće oznake
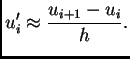
![]() s
s ![]()
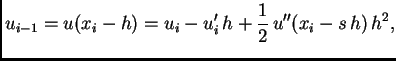
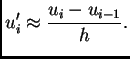
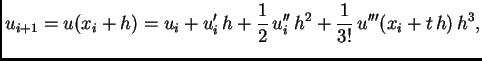
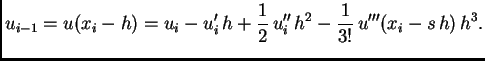
![$\displaystyle u'_i = \frac{u_{i+1}-u_{i-1}}{2\,h} +
\frac{h^2}{3!}\,\left[u'''(x_i+t\,h) + u'''(x_i-s\,h)\right],$](img3279.png)
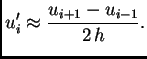
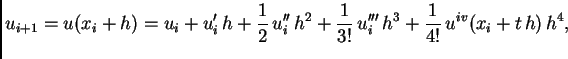
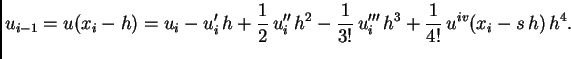
![$\displaystyle u_{i+1} + u_{i-1} = 2\,u_i + u''_i\,h^2 +
\frac{h^4}{4!}\,\left[u^{iv}(x_i+t\,h) +
u^{iv}(x_i-s\,h)\right].$](img3283.png)
![$\displaystyle u''_i = \frac{u_{i+1}-2\,u_i+u_{i-1}}{h^2} -
\frac{h^2}{4!}\,\left[u^{iv}(x_i+t\,h) +
u^{iv}(x_i-s\,h)\right].$](img3285.png)
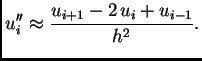
![]() diferencijalna jednadžba iz rubnog problema glasi
diferencijalna jednadžba iz rubnog problema glasi
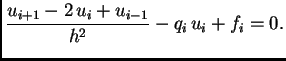
![\begin{displaymath}
% latex2html id marker 40728
A(h) = \left[
\begin{array}{cc...
...0 & 0 & \cdots{} & -1 & (1+h^2\,q_{n-1})
\end{array}
\right],\end{displaymath}](img3300.png)
![]() kažemo da je
striktno dijagonalno dominantna ako je
kažemo da je
striktno dijagonalno dominantna ako je
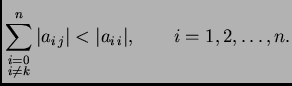
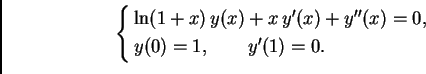
![]() na deset jednakih dijelova, tako da
je korak
na deset jednakih dijelova, tako da
je korak ![]() Čvorovi su
Čvorovi su
![]() Stavimo
Stavimo
![]() Za prvu derivaciju upotrebimo desnu
aproksimaciju, osim na desnom rubu, gdje uzmemo lijevu. U svakom
unutrašnjem čvoru zamijenimo derivacije odgovarajućim
aproksimacijama. Dobivamo sustav jednadžbi
Za prvu derivaciju upotrebimo desnu
aproksimaciju, osim na desnom rubu, gdje uzmemo lijevu. U svakom
unutrašnjem čvoru zamijenimo derivacije odgovarajućim
aproksimacijama. Dobivamo sustav jednadžbi