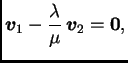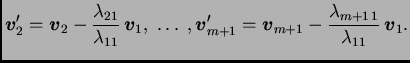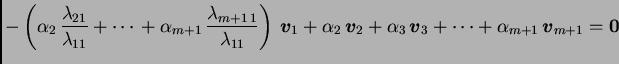Next: Sustavi linearnih algebarskih jednadžbi
Up: Vektori i matrice
Previous: Produkt matrice i vektora.
Sadržaj
Indeks
Baza
Vidjeli smo da se vektorstupci u
 i
i
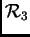 mogu identificirati
s radijvektorima, i prema tome crtati u ravnini i prostoru. U ravnini,
preciznije u vektorskom prostoru radijvektora u ravnini, bilo koja dva
nekolinearna vektora čine bazu. Na slici 1.8 se vidi kako
se vektor
mogu identificirati
s radijvektorima, i prema tome crtati u ravnini i prostoru. U ravnini,
preciznije u vektorskom prostoru radijvektora u ravnini, bilo koja dva
nekolinearna vektora čine bazu. Na slici 1.8 se vidi kako
se vektor
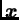 može prikazati kao linearna kombinacija dva
nekolinearna vektora
može prikazati kao linearna kombinacija dva
nekolinearna vektora
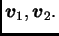
Slika 1.8:
Baza u
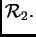
|
|
Također, u vektorskom prostoru radijvektora u prostoru bilo koja tri
nekomplanarna vektora čine bazu. Na slici 1.9 se vidi kako
se vektor
 može prikazati kao linearna kombinacija tri
nekomplanarna vektora
može prikazati kao linearna kombinacija tri
nekomplanarna vektora
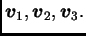
Slika 1.9:
Baza u
|
|
Primjer 1.7
Neka su zadani vektori u
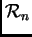
Ovi vektori čine bazu u
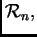
i ta baza se
zove
kanonska baza u
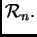
Rješenje. Zaista,
i također
povlači
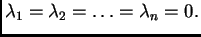
Prema tome ovi
vektori razapinju
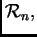
i linearno su nezavisni.
Primjer 1.8
Neka su zadane matrice u
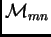
One čine bazu u
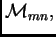
i ta baza se
zove
kanonska baza u
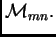
Rješenje. Zaista,
i također
povlači
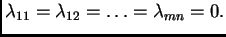
Prema tome ovi
vektori razapinju
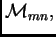
i linearno su nezavisni.
Teorem 2
Svaki vektor se na jedinstven način prikazuje kao linearna
kombinacija vektora baze.
Dokaz. Neka je 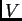 vektorski
prostor, neka je
vektorski
prostor, neka je
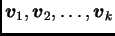 baza u
baza u 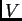 i neka je
i neka je
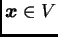 proizvoljan. Zbog drugog svojstva baze
imamo
proizvoljan. Zbog drugog svojstva baze
imamo
Pretpostavimo da je također
Tada je
Zbog linearne nezavisnosti
baze, slijedi
Dakle, nije moguće da
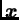 ima dva
različita prikaza u
ima dva
različita prikaza u 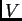 u odnosu na izabranu bazu.
u odnosu na izabranu bazu.
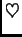
Teorem 3
[
1, str. 141]
Neka je u vektorskom prostoru
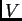
dano
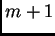
međusobno različitih
vektora
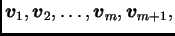
i neka se
svaki od njih može napisati kao linearna kombinacija od
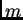
vektora
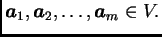
Tada su vektori
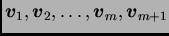
linearno zavisni.
Dokaz. Teorem ćemo dokazati
matematičkom indukcijom. Za 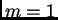 tvrdnja vrijedi, jer iz
tvrdnja vrijedi, jer iz
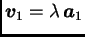 i
i
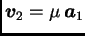 slijedi
slijedi
odakle
pa su vektori
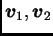 linearno zavisni. Ako je
linearno zavisni. Ako je
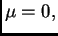 onda se ne može dijeliti s
onda se ne može dijeliti s 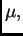 no u tom slučaju je
no u tom slučaju je
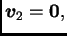 pa su vektori
pa su vektori
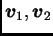 linearno zavisni jer vrijedi
Pretpostavimo da tvrdnja vrijedi za svaki prirodni broj
linearno zavisni jer vrijedi
Pretpostavimo da tvrdnja vrijedi za svaki prirodni broj 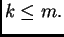 Dokažimo da tvrdnja vrijedi i za
Dokažimo da tvrdnja vrijedi i za 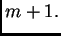 Po pretpostavci imamo
Kad bi svaki koeficijent uz
Po pretpostavci imamo
Kad bi svaki koeficijent uz
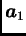 bio jednak
nuli, onda bismo imali situaciju da su vektori
bio jednak
nuli, onda bismo imali situaciju da su vektori
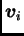 linearne kombinacije od
linearne kombinacije od 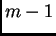 vektora, pa bi po pretpostavci indukcije
bili linearno zavisni. Stoga možemo pretpostaviti da je na primjer
vektora, pa bi po pretpostavci indukcije
bili linearno zavisni. Stoga možemo pretpostaviti da je na primjer
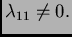 Pomnožimo prvu jednadžbu s
Pomnožimo prvu jednadžbu s
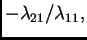 i dodajmo je drugoj. Time vektor
i dodajmo je drugoj. Time vektor
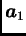 iščezne iz druge jednadžbe. Zatim, pomnožimo
prvu jednadžbu s
iščezne iz druge jednadžbe. Zatim, pomnožimo
prvu jednadžbu s
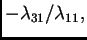 i dodajmo je
trećoj. Time vektor
i dodajmo je
trećoj. Time vektor
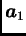 iščezne iz treće
jednadžbe, itd. Nakon tog postupka druga, treća i ostale jednadžbe
izgledaju ovako
Po pretpostavci indukcije slijedi da su vektori
iščezne iz treće
jednadžbe, itd. Nakon tog postupka druga, treća i ostale jednadžbe
izgledaju ovako
Po pretpostavci indukcije slijedi da su vektori
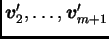 linearno zavisni. Pri
tom je
To
znači da postoje brojevi
linearno zavisni. Pri
tom je
To
znači da postoje brojevi
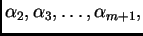 od kojih je barem
jedan različit od nule, takvi da je
odnosno vrijedi
za barem jedan
od kojih je barem
jedan različit od nule, takvi da je
odnosno vrijedi
za barem jedan
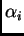 različit od nule, pa su prema
tome vektori
različit od nule, pa su prema
tome vektori
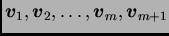 linearno zavisni. Kako su time ispunjene pretpostavke aksioma
matematičke indukcije, tvrdnja vrijedi za svaki prirodni broj
linearno zavisni. Kako su time ispunjene pretpostavke aksioma
matematičke indukcije, tvrdnja vrijedi za svaki prirodni broj 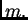
Posljedice.
- Svaka četiri vektora u
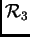 su linearno zavisna.
su linearno zavisna.
(Svaki se može napisati kao linearna kombinacija
vektora kanonske baze, kojih ima tri)
- Ako su vektori
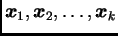 iz
iz
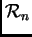 linearno
nezavisni, onda je
linearno
nezavisni, onda je 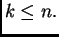
(Kanonska baza ima
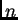 elemenata)
elemenata)
- Ako je svaki vektor iz
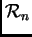 linearna kombinacija vektora
linearna kombinacija vektora
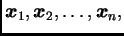 onda su vektori
onda su vektori
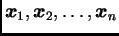 linearno nezavisni, i prema tome čine bazu.
linearno nezavisni, i prema tome čine bazu.
(Ako
su linearno zavisni, onda onda se barem jedan od njih može
prikazati kao linearna kombinacija ostalih 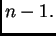 Tada se i svaki
od
Tada se i svaki
od 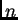 vektora kanonske baze može prikazati kao linearna
kombinacija od
vektora kanonske baze može prikazati kao linearna
kombinacija od 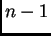 vektora, pa su vektori kanonske baze linearno
zavisni. Kontradikcija)
vektora, pa su vektori kanonske baze linearno
zavisni. Kontradikcija)
- Svaka baza u vektorskom prostoru
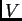 ima jednaki broj elemenata.
ima jednaki broj elemenata.
(Vektora u bazi ne može biti više nego što ih
ima u kanonskoj bazi, jer bi u tom slu čaju bili linearno
zavisni. Ne može ih biti niti manje, jer se svaki vektor
kanonske baze može napisati kao njihova linearna kombinacija, pa
bi u tom slučaju vektori kanonske baze bili linearno zavisni, što
je u kontradikciji s definicijom baze.)
Broj vektora u bazi se
zove dimenzija prostora 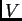 i označava s
i označava s
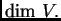
-






Next: Sustavi linearnih algebarskih jednadžbi
Up: Vektori i matrice
Previous: Produkt matrice i vektora.
Sadržaj
Indeks
2001-10-26
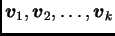 su linearno nezavisni.
su linearno nezavisni.
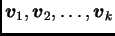 razapinju vektorski prostor
razapinju vektorski prostor
 , tj. svaki vektor iz
, tj. svaki vektor iz  može se napisati kao linearna
kombinacija vektora
može se napisati kao linearna
kombinacija vektora
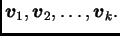
![]() i
i
![]() mogu identificirati
s radijvektorima, i prema tome crtati u ravnini i prostoru. U ravnini,
preciznije u vektorskom prostoru radijvektora u ravnini, bilo koja dva
nekolinearna vektora čine bazu. Na slici 1.8 se vidi kako
se vektor
mogu identificirati
s radijvektorima, i prema tome crtati u ravnini i prostoru. U ravnini,
preciznije u vektorskom prostoru radijvektora u ravnini, bilo koja dva
nekolinearna vektora čine bazu. Na slici 1.8 se vidi kako
se vektor
![]() može prikazati kao linearna kombinacija dva
nekolinearna vektora
može prikazati kao linearna kombinacija dva
nekolinearna vektora
![]()
![]() može prikazati kao linearna kombinacija tri
nekomplanarna vektora
može prikazati kao linearna kombinacija tri
nekomplanarna vektora
![]()
![% latex2html id marker 30842
$\displaystyle \boldsymbol{e}_1=\left[\begin{array}...
...mbol{e}_n=\left[\begin{array}{c} 0 \\ 0 \\ \vdots \\ 1
\end{array} \right].$](img285.png)
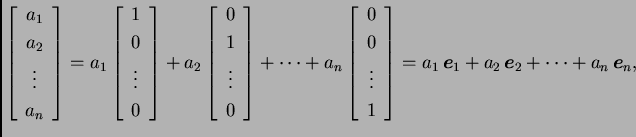
![% latex2html id marker 30850
$\displaystyle \lambda_1\left[\begin{array}{c}
1 \...
...} \right]=\left[\begin{array}{c}
0 \\ 0 \\ \vdots \\ 0
\end{array} \right]$](img287.png)
![% latex2html id marker 30859
$\displaystyle E_{11}= \left[ \begin{array}{cccc}
...
...
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & 1 \end{array}\right] .$](img289.png)
![% latex2html id marker 30865
$\displaystyle \left[\begin{array}{cccc}
a_{11} & ...
...vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & 0
\end{array} \right] +$](img291.png)
![% latex2html id marker 30867
$\displaystyle \cdots+a_{mn}\left[\begin{array}{ccc...
...s & 1
\end{array} \right]=a_{11}\,E_{11}+a_{12}\,E_{12}+\cdots+a_{mn}\,E_{mn},$](img292.png)
![% latex2html id marker 30869
$\displaystyle \lambda_{11}\left[\begin{array}{cccc...
...
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & 1
\end{array} \right]$](img293.png)
![% latex2html id marker 30871
$\displaystyle =\left[\begin{array}{cccc}
\lambda_...
...
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & 0
\end{array} \right]$](img294.png)
![]() vektorski
prostor, neka je
vektorski
prostor, neka je
![]() baza u
baza u ![]() i neka je
i neka je
![]() proizvoljan. Zbog drugog svojstva baze
imamo
proizvoljan. Zbog drugog svojstva baze
imamo
![]() tvrdnja vrijedi, jer iz
tvrdnja vrijedi, jer iz
![]() i
i
![]() slijedi
slijedi