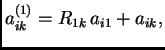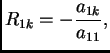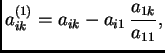Next: Rang matrice
Up: Gaussov postupak eliminacije
Previous: Gaussov postupak eliminacije
Sadržaj
Indeks
Neka je dan štap (greda, ploča, štapna konstrukcija). Pod
djelovanjem sila štap doživi progib. Interesira nas iz zadanog
progiba naći sile koje koje su uzrokovale taj progib.
Odredimo 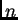 točaka na štapu, koje ćemo zvati čvorovi.
Promatrat ćemo štap kao da je njegova masa koncentrirana u tih
točaka na štapu, koje ćemo zvati čvorovi.
Promatrat ćemo štap kao da je njegova masa koncentrirana u tih 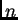 točaka. Prema tome pretpostavljamo da sile mogu djelovati samo u
čvorovima. Shodno tome i progib promatramo samo u čvorovima. Pri tom
polazimo od dvije osnovne pretpostavke, koje u fizici predstavljaju
princip superpozicije sila, a u matematici se
to zove svojstvo
linearnosti.
točaka. Prema tome pretpostavljamo da sile mogu djelovati samo u
čvorovima. Shodno tome i progib promatramo samo u čvorovima. Pri tom
polazimo od dvije osnovne pretpostavke, koje u fizici predstavljaju
princip superpozicije sila, a u matematici se
to zove svojstvo
linearnosti.
- Pri istovremenom djelovanju dviju sila odgovarajući progibi se zbrajaju.
- Koliko puta povećamo silu, toliko puta se poveća progib.
Označimo s 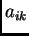 progib u čvoru
progib u čvoru 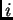 uslijed djelovanja jedinične
sile u čvoru
uslijed djelovanja jedinične
sile u čvoru 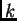 (sl. 1.10).
(sl. 1.10).
Slika 1.10:
Pomak štapa pod djelovanjem jedinične sile u čvoru 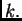
|
|
Označimo s
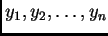 ukupne progibe, a s
ukupne progibe, a s
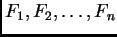 sile u čvorovima (sl. 1.11).
sile u čvorovima (sl. 1.11).
Slika 1.11:
Pomak štapa pod djelovanjem različitih sila u čvorovima.
|
|
Tada vrijede sljedeće jednadžbe
Vidimo da problem nalaženja sila iz zadanih progiba vodi na
rješavanje sustava linearnih algebarskih jednadžbi.
Pretpostavimo sada da u čvoru 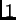 djeluje sila
djeluje sila 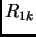 takva da
poništava utjecaj jedinične sile u čvoru
takva da
poništava utjecaj jedinične sile u čvoru 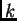 na čvor
na čvor 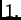
Slika 1.12:
Pomak štapa pod djelovanjem jedinične sile u čvoru 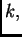 nakon uravnoteženja u čvoru
nakon uravnoteženja u čvoru 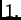
|
|
U ovoj situaciji označimo s
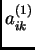 progib u čvoru
progib u čvoru 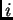 uslijed djelovanja jedinične sile u čvoru
uslijed djelovanja jedinične sile u čvoru 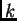 (sl.
1.12). Tada vrijedi
za
(sl.
1.12). Tada vrijedi
za
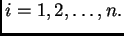 Specijalno u čvoru
Specijalno u čvoru 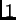 imamo
Odatle slijedi
pa je
za
imamo
Odatle slijedi
pa je
za
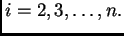 Ako tako učinimo za svaki
Ako tako učinimo za svaki
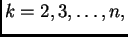 dobijemo koeficijente nakon prvog koraka u Gaussovoj metodi. Slično
bi se moglo pokazati da se koeficijenti nakon drugog koraka dobiju kad
u prva dva čvora djeluju sile koje poništavaju progibe uslijed
djelovanja jedinične sile u ostalim čvorovima, itd. Detaljnije o
tome u [8].
dobijemo koeficijente nakon prvog koraka u Gaussovoj metodi. Slično
bi se moglo pokazati da se koeficijenti nakon drugog koraka dobiju kad
u prva dva čvora djeluju sile koje poništavaju progibe uslijed
djelovanja jedinične sile u ostalim čvorovima, itd. Detaljnije o
tome u [8].





Next: Rang matrice
Up: Gaussov postupak eliminacije
Previous: Gaussov postupak eliminacije
Sadržaj
Indeks
2001-10-26
![]() točaka na štapu, koje ćemo zvati čvorovi.
Promatrat ćemo štap kao da je njegova masa koncentrirana u tih
točaka na štapu, koje ćemo zvati čvorovi.
Promatrat ćemo štap kao da je njegova masa koncentrirana u tih ![]() točaka. Prema tome pretpostavljamo da sile mogu djelovati samo u
čvorovima. Shodno tome i progib promatramo samo u čvorovima. Pri tom
polazimo od dvije osnovne pretpostavke, koje u fizici predstavljaju
princip superpozicije sila, a u matematici se
to zove svojstvo
linearnosti.
točaka. Prema tome pretpostavljamo da sile mogu djelovati samo u
čvorovima. Shodno tome i progib promatramo samo u čvorovima. Pri tom
polazimo od dvije osnovne pretpostavke, koje u fizici predstavljaju
princip superpozicije sila, a u matematici se
to zove svojstvo
linearnosti.
![]() progib u čvoru
progib u čvoru ![]() uslijed djelovanja jedinične
sile u čvoru
uslijed djelovanja jedinične
sile u čvoru ![]() (sl. 1.10).
(sl. 1.10).
![]() djeluje sila
djeluje sila ![]() takva da
poništava utjecaj jedinične sile u čvoru
takva da
poništava utjecaj jedinične sile u čvoru ![]() na čvor
na čvor ![]()