Teorem 5
(Teorem o rangu).
Broj linearno nezavisnih redaka proizvoljne matrice
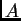
tipa
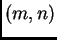
jednak je broju njezinih linearno nezavisnih stupaca. Taj broj se
zove
rang
matrice 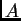
, i označava se sa
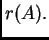
Dokaz. Množeći matricu 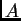 dovoljan (konačan) broj puta s lijeva i s desna s odgovarajućim
elementernim matricama, matrica
dovoljan (konačan) broj puta s lijeva i s desna s odgovarajućim
elementernim matricama, matrica 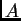 se može svesti na oblik
se može svesti na oblik
gdje je 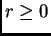 broj jedinica. Stupci (reci) u
kojima se pojavljuju jedinice su
linearno nezavisni. Dokaz je isti kao dokaz linearne nezavisnosti
kanonske baze (primjer 1.7). Ako tim stupcima
(recima) dodamo stupac (redak) sastavljen od samih nula, stupci
(reci) će postati linearno zavisni, jer množeći taj stupac
(redak) s
broj jedinica. Stupci (reci) u
kojima se pojavljuju jedinice su
linearno nezavisni. Dokaz je isti kao dokaz linearne nezavisnosti
kanonske baze (primjer 1.7). Ako tim stupcima
(recima) dodamo stupac (redak) sastavljen od samih nula, stupci
(reci) će postati linearno zavisni, jer množeći taj stupac
(redak) s 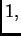 a druge s nulom, dobivamo nulstupac (nulredak).
Tako imamo
a druge s nulom, dobivamo nulstupac (nulredak).
Tako imamo 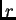 linearno nezavisnih stupaca i također
linearno nezavisnih stupaca i također 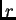 linearno
nezavisnih redaka. Time smo dokazali teorem o rangu.
linearno
nezavisnih redaka. Time smo dokazali teorem o rangu.
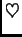
Dokazom ovog teorema smo ujedno dobili metodu za ispitivanje ranga
matrice. Treba elementarnim operacijama svesti matricu na oblik kao u
dokazu teorema, i zatim očitati broj jedinica na dijagonali.
Primjer 1.15
Odrediti rang slijedeće matrice u ovisnosti o
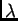
Rješenje. Najprije zamjenom redaka i stupaca imamo
Sada množenjem prvog retka redom s
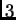
i
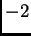
i dodavanjem trećem i
četvrtom retku dobivamo
Množenjem prvog stupca s odgovarajućim brojevima i dodavanjem
ostalim stupcima možemo u prvom retku dobiti same nule. Budući da su
u ostalim recima prvog stupca nule, to neće imati nikakvog utjecaja
na elemente u ostalim recima. Zato smijemo jednostavno u prvom retku
upisati nule. Zatim pomnožimo četvrti redak redom s
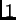
i s
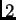
i
dodamo drugom i trećem retku. Nakon toga četvrti redak preselimo na
mjesto drugog.
Sada s drugim stupcem možemo anulirati elemente u drugom retku, a da
se ništa drugo ne promijeni. Tako imamo konačno
Korijeni polinoma
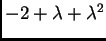
su
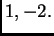
Prema tome, ako je
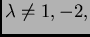
rang je
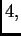
ako je
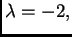
rang je
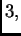
ako je
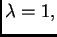
rang je
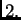
Važna napomena: kad se vrše elementarne transformacije nad matricom
u kojoj ima parametara čiju točnu vrijednost ne znamo, treba paziti
da su operacije koje vršimo korektne, bez obzira na to koju stvarnu
vrijednost ima parametar. Na pr. ne smijemo dijeliti redak (stupac) s
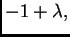 jer to može biti nula.
jer to može biti nula.
![]() Njezine stupce, i njezine retke možemo
shvatiti kao vektore.
Njezine stupce, i njezine retke možemo
shvatiti kao vektore.
![% latex2html id marker 31344
$\displaystyle A=\left[\begin{array}{cccc}
\boldsy...
...ol{a}_{2\,\cdot} \\ \vdots \\ \boldsymbol{a}_{m\,\cdot}
\end{array} \right],$](img423.png)
![]() broj
linearno nezavisnih stupaca matrice
broj
linearno nezavisnih stupaca matrice ![]() Radi jednostavnosti
pretpostavimo da su to prvih
Radi jednostavnosti
pretpostavimo da su to prvih ![]() stupaca
stupaca
![]() dovoljan (konačan) broj puta s lijeva i s desna s odgovarajućim
elementernim matricama, matrica
dovoljan (konačan) broj puta s lijeva i s desna s odgovarajućim
elementernim matricama, matrica ![]() se može svesti na oblik
se može svesti na oblik
![% latex2html id marker 31432
$\displaystyle \left[\begin{array}{cccccc}
1 & \cd...
...ots & \ddots & \vdots \\
0 & \cdots & 0 & 0 & \cdots & 0
\end{array}\right],$](img449.png)
![% latex2html id marker 31445
$\displaystyle A=\left[ \begin{array}{rrrrrr}
1 & ...
... 1 \\
1 & 1 & -1 & 0 & 1 & -1 \\
2 & 1 & 1 & 1 & 1 & 3
\end{array}\right].$](img453.png)
![% latex2html id marker 31447
$\displaystyle \left[ \begin{array}{rrrrrr}
1 & 0 ...
... & 1 & 5 & 1 & -3 \\
0 & 0 & 0 & 1 &\frac{1}{4} & -1
\end{array} \right]\sim$](img454.png)
![% latex2html id marker 31449
$\displaystyle \sim\left[\begin{array}{rrrrrr}
1 &...
...& 0 \\
0 & 0 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0
\end{array} \right],$](img455.png)
![% latex2html id marker 31456
$\displaystyle A = \left[\begin{array}{rrrr}
1-\la...
...lambda+\lambda^2 & -2+2\lambda-\lambda^2-\lambda^3 & 2 & 5
\end{array}\right].$](img457.png)
![% latex2html id marker 31458
$\displaystyle A \sim \left[\begin{array}{rrrr}
1 ...
...2+3\lambda+\lambda^2 & -2+2\lambda-\lambda^2-\lambda^3 \\
\end{array}\right].$](img458.png)
![% latex2html id marker 31464
$\displaystyle A \sim \left[\begin{array}{rrrr}
1 ...
... & -2+\lambda+\lambda^2 & 2\lambda-\lambda^2-\lambda^3 \\
\end{array}\right].$](img459.png)
![% latex2html id marker 31470
$\displaystyle A \sim \left[\begin{array}{rrrr}
1 ...
...& -1+\lambda & 0 \\
0 & 0 & 0 & -2+\lambda+\lambda^2 \\
\end{array}\right].$](img461.png)
![% latex2html id marker 31472
$\displaystyle A \sim \left[\begin{array}{rrrr}
1 ...
...& -1+\lambda & 0 \\
0 & 0 & 0 & -2+\lambda+\lambda^2 \\
\end{array}\right].$](img462.png)
![]() jer to može biti nula.
jer to može biti nula.