Zaključak.

Ako s $X_0$ označimo skup svih rješenja pripadnog homogenog, a s $X_b$ skup svih rješenja nehomogenog sustava, onda je $X_0$ vektorski prostor dimenzije $n-r,$ gdje je $r$ rang matrice sustava, i vrijedi

$$X_0 = \{\lambda_1\,\boldsymbol{u}_1 ... ...boldsymbol{u}_{n-r};\,\lambda_1,\lambda_2,\cdots,\lambda_{n-r}\in \mathbb{R}\},$$

gdje $\boldsymbol{u}_1, \boldsymbol{u}_2, \ldots, \boldsymbol{u}_{n-r}$ čine bazu u $X_0,$ a $\lambda_1, \lambda_2, \ldots, \lambda_{n-r}$ su proizvoljni brojevi. Također vrijedi

$$X_b = \{\boldsymbol{x}_p+\boldsymbol{u};\,\boldsymbol{u}\in X_0\}.$$

Primjer 1.22   Riješiti sustav jednadžbi

$$\begin{array}{rrrrrrr} 2\,x_1 & +3\... ... & 1 \\ 5\,x_1 & -3\,x_2 & +2\,x_3 & +7\,x_4 & -\,x_5 & = & -8. \end{array}$$

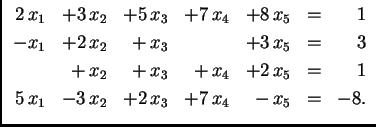
Rješenje. Rješenje ovog sustava je svaka uređena petorka (vektorstupac)

$$\boldsymbol{x}= \left[ \begin{array}{r} x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \end{array} \right],$$

koja zadovoljava svaku jednadžbu. Gauss-Jordanovim postupkom dolazimo do sustava

$$x_1\hspace{.8cm}+x_3+2\,x_4+x_5 = -1$$

$$x_2+x_3+x_4+2\,x_5 = 1.$$

Odatle,

$$x_1 = -1-x_3-2\,x_4-x_5$$

$$x_2 = 1-x_3-x_4-2\,x_5,$$

pa je rješenje

$$\boldsymbol{x}=\left[ \begin{array}{... ...x_5 \left[ \begin{array}{r} -1 \\ -2 \\ 0 \\ 0 \\ 1 \end{array} \right].$$

Pri tom je $\left[ \begin{array}{r} -1 \\ 1 \\ 0 \\ 0 \\ 0 \end{array} \right]$ partikularno rješenje, a vektori $\left[ \begin{array}{r} -1 \\ -1 \\ 1 \\ 0 \\... ...],\; \left[ \begin{array}{r} -1 \\ -2 \\ 0 \\ 0 \\ 1 \end{array} \right]$

čine bazu u vektorskom prostoru svih rješenja pripadnog homogenog sustava.

Primjer 1.23   Diskutirati i riješiti sljedeći sustav jednadžbi u odnosu na parametar $a.$

$$x_1+x_2+x_3 = 6$$

$$a\,x_1+4x_2+x_3 = 5$$

$$6x_1+(a+2)x_2+2x_3 = 13.$$

Rješenje. Proširena matrica sustava je

$$A_b = \left[ \begin{array}{cccc} 1 & 1 & 1 & 6 \\ a & 4 & 1 & 5 \\ 6 & a+2 & 2 & 13 \\ \end{array} \right].$$

Množimo prvi redak redom s $-a,-6,$ i dodamo drugom, odnosno trećem retku. Zatim tako dobiveni drugi redak dodamo trećem. Konačno prvim stupcem anuliramo elemente u prvom retku. Dobijemo

$$A_b \sim \left[ \begin{array}{cccc}... ... 0 & 4-a & 1-a & 5-6a \\ 0 & 0 & -(3+a) & -6(3+a) \\ \end{array} \right].$$

Sada ne smijemo s drugim stupcem anulirati elemente u drugom retku, jer se može dogoditi da je $4-a=0.$ S elementarnim transformacijama smo gotovi, i treba provesti diskusiju.

Ako je $a=-3,$ onda je $r(A)=r(A_b)=2,$ pa imamo beskonačno mnogo rješenja (jednoparametarsko rješenje). Da dobijemo rješenje u tom slučaju, moramo se vratiti korak natrag, prije anuliranja elemenata u prvom retku, i uvrstiti $a=-3.$

$$A_b \sim \left[ \begin{array}{cccc} 1 & 1 & 1 & 6 \\ 0 & 7 & 4 & 23 \\ 0 & 0 & 0 & 0 \\ \end{array} \right].$$

Zatim pomnožiti drugi redak s $-\frac{1}{7}$ i dodati ga prvom.

$$A_b \sim \left[ \begin{array}{cccc}... ... \frac{19}{7} \\ 0 & 7 & 4 & 23 \\ 0 & 0 & 0 & 0 \\ \end{array} \right].$$

Odatle se čita rješenje

$$\left[ \begin{array}{c} x_1 \\ x_... ...x_3\,\left[ \begin{array}{c} -\frac{3}{7} \\ -4 \\ 1 \end{array} \right].$$

Ako je $a=4,$ onda je $r(A)=2,r(A_b)=3,$ pa ne postoji rješenje.

Inače je $r(A)=r(A_b)=3,$ i tada imamo jedinstveno rješenje, koje dobijemo nakon Gaussovog postupka.

$$A_b \sim \left[ \begin{array}{cccc}... ... 0 & 4-a & 1-a & 5-6a \\ 0 & 0 & -(3+a) & -6(3+a) \\ \end{array} \right].$$

Iz zadnje jednadžbe čitamo da je $x_3=6.$ Uvrštavanjem u drugu dobijemo $x_2=\frac{1}{a-4},$ i konačno iz prve jednadžbe slijedi $x_1 =\frac{1}{4-a}.$