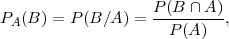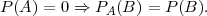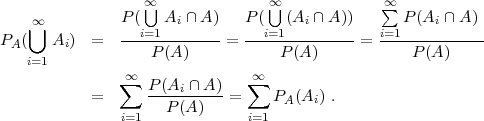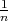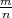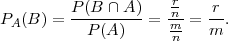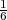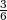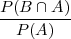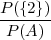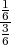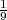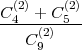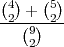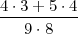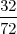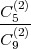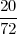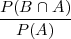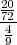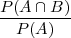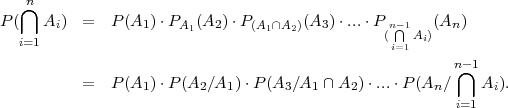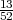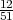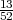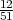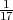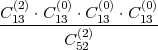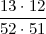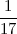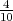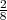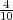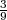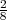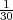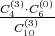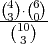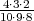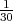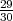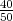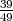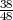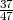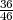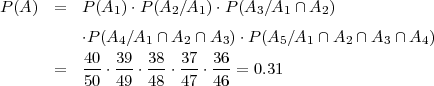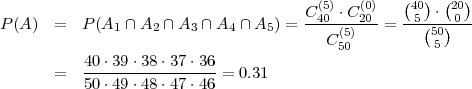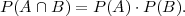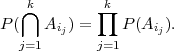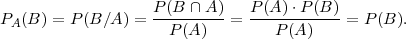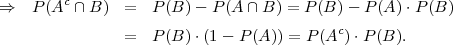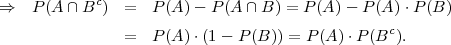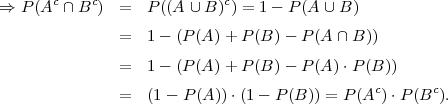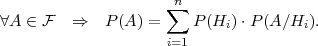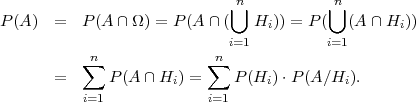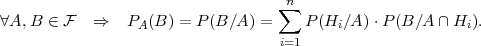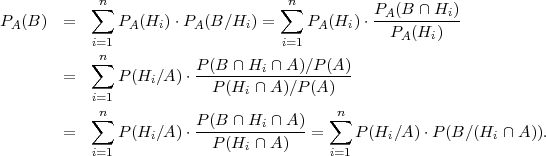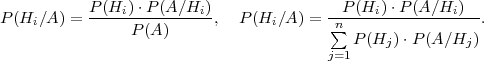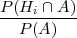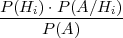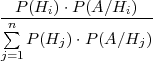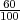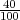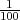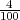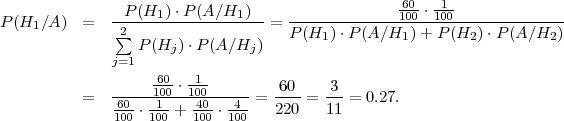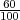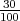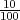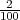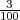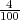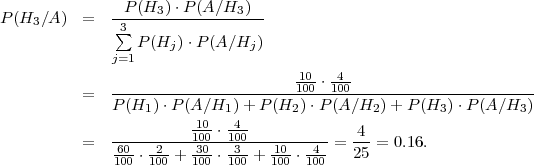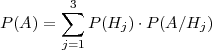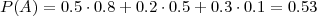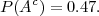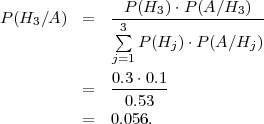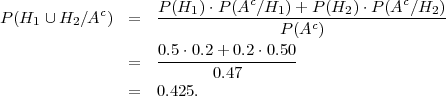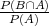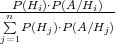Poglavlje 4
UVJETNA VJEROJATNOST
Thomas Bayes (1702 - 1762) uvodi pojam uvjetne vjerojatnosti: vjerojat- nost da se
dogodi dogadaj B ako se dogodio dogadaj A jednaka je kvocijentu vjerojatnosti da se
dogode dogadaji i A i B i vjerojatnosti dogadaja A.
MOTIV 4.1
Kontolor u tvornici daje nakon vizualnog pregleda tri tipa odluke: 1) proizvod
je defektan i šalje se na daljnje pretrage 2) sumnja se da je proizvod defektan
i šalje se na daljnje pretrage 3) proizvod je ispravan. Pokazalo se dosada da je
kontolor bio u pravu kad je odlučio: o neispravnosti u 80% slučajeva, o sumnji na
neispravnost u 50% slučajeva, a o ispravnosti proizvoda a u 90% slučajeva.
U toku jednog dana kontrolor donosi prvu odluku kod 50%, drugu kod 20%
i treću dijagnozu kod 30% proizvoda. (a) Odredite vjerojatnost neispravnosti
proizvoda. (b) Odredite vjerojatnost pogrešne odluke tj. odluke kontolora da je
proizvod ispravan a on je zaista neispravan. (c) Odredite vjerojatnost nepotrebnih
troškova ili slanja na daljnje pretrage proizvoda ako je zaista ispravan.
Definicija 4.1 (UVJETNA VJEROJATNOST)
Neka je (Ω, ,P) vjerojatnosni prostor i neka je A ∈
,P) vjerojatnosni prostor i neka je A ∈ takav da je P(A) > 0. Tada
funkciju PA :
takav da je P(A) > 0. Tada
funkciju PA :  → [0,1] zovemo uvjetna vjerojatnost a definiramo ∀ B ∈
→ [0,1] zovemo uvjetna vjerojatnost a definiramo ∀ B ∈ kao
kao
vjerojatnost od B uz uvjet da se dogodio A.
tko želi znati više
TEOREM 4.1 Uvjetna vjerojatnost je vjerojatnost. Zadovoljava uvjete
(UP1) PA(B) ≥ 0,B ⊂ (svojstvo nenegativnosti);
(svojstvo nenegativnosti);
(UP2) PA(Ω) = 1 (svojstvo normiranosti);
(UP3) Ai ∈ , i ∈ ℕ, Ai ∩ Aj = ∅, i≠j ⇒ PA(⋃
i=1∞Ai) = ∑
i=1∞PA(Ai)
, i ∈ ℕ, Ai ∩ Aj = ∅, i≠j ⇒ PA(⋃
i=1∞Ai) = ∑
i=1∞PA(Ai)
(svojstvo prebrojive aditivnosti).
Dokaz: (UP3) Ai ∈ , i ∈ N, Ai ∩ Aj = ∅, i≠j
, i ∈ N, Ai ∩ Aj = ∅, i≠j
⇒ Ai ∩ A ∈ , i ∈ N, (Ai ∩ A) ∩ (Aj ∩ A) = ∅, i≠j
, i ∈ N, (Ai ∩ A) ∩ (Aj ∩ A) = ∅, i≠j
PRIMJER 4.1 Bacamo kocku. Kolika je vjerojatnost da će ”pasti” paran broj
pod uvjetom da je je ”pao” broj manji od 4?
Rješenje: Ω = {ω1,...,ω6} = {1,2,3,4,5,6}, P({ωi}) = 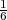 .
.
A = {1,2,3}, P(A) > 0, P(A) = 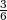 B = {2,4,6}, PA(B) =?
B = {2,4,6}, PA(B) =?
PA(B) = 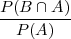 =
= 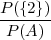 =
= 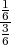 =
=  .
.
PRIMJER 4.2 Izabiremo slučajno dva broja izmedu brojeva od 1 do 9. Ako je
njihov zbroj paran broj kolika je vjerojatnost da su oba neparna?
Rješenje:
Ω = {{ωi,ωj} : ωi≠ωj,ω1,...,ω9 ∈{1,2,3,4,5,6,7,8,9}}, P({ωi}) = 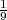 .
.
A ⊂ Ω, A = {ωi1,ωi2}, ωi1 + ωi2 = paran,
P(A) = 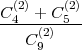 =
= 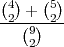 =
= 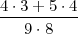 =
= 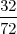 =
= 
B ⊂ Ω, B = {ωi1,ωi2}, ωi1,ωi2 = neparni, PA(B) =?
P(B ∩ A) = 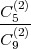 =
= 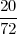 , PA(B) =
, PA(B) = 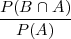 =
= 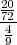 =
=  .
.
TEOREM 4.2 (FORMULA PRODUKTA VJEROJATNOSTI)
Vjerojatnost produkta (presjeka) dva dogadaja (A ∩ B) jednaka je produktu
vjerojatnosti jednog od njih i uvjetne vjerojatnosti drugog, pod uvjetom da se prvi
dogodio.

Dokaz:
Ako je P(A) > 0, prema definiciji uvjetne vjerojatnosti PA :
PA(B) = 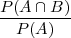 ⇒ P(A ∩ B) = P(A) ⋅ PA(B).
⇒ P(A ∩ B) = P(A) ⋅ PA(B).
Ako je P(A) = 0 ⇒ PA(B) = P(B) ⇒ P(A ∩ B) = P(A) ⋅ P(B) = 0.
TEOREM 4.3 (FORMULA PRODUKTA VJEROJATNOSTI*)
Vjerojatnost produkta (presjeka) n dogadaja (A1 ∩ A2 ∩ ... ∩ An) jednaka je
Dokaz:Pomoću AMI.
PRIMJER 4.3 Iz špila karata (52 karte) izvlačimo jednu za drugom dvije karte.
Kolika je vjerojatnost da obe karte budu pik?
Rješenje: A=”obje karte su pik”
A1=”prva je pik”, P(A1) = 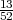
A2=”druga je pik”, P(A2∕A1) = 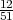
A = A1 ∩ A2.
Prema formuli produkta (presjeka) vjerojatnosti:
P(A) = P(A1 ∩ A2) = P(A1) ⋅ P(A2∕A1) = 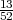 ⋅
⋅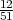 =
= 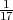 .
.
Ili direktno (pomoću formule za uzorak bez vraćanja):
P(A1 ∩ A2) = 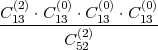 =
= 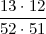 =
= 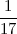 .
.
PRIMJER 4.4 U kutiji se nalazi 10 kuglica: 6 bijelih i 4 crne. Izvlačimo 3
kuglice jednu za drugom. Kolika je vjerojatnost da će bar jedna od njih biti bijela?
Rješenje: A=”izvučena bar jedna bijela”, Ac=”izvučene sve crne”,
A1=”prva izvučena crna”, P(A1) = 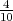
A2=”druga izvučena crna”, P(A1∕A2) =  ,
,
A3=”treća izvučena crna”, P(A3∕A1 ∩ A2) = 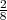 .
.
Prema formuli produkta (presjeka) vjerojatnosti
P(Ac) = P(A1) ⋅ P(A2∕A1) ⋅ P(A3∕A1 ∩ A2) = 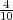 ⋅
⋅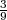 ⋅
⋅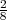 =
= 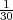 .
.
Ili direktno (pomoću formule za uzorak bez vraćanja):
P(Ac) = P(A1 ∩ A2 ∩ A3) = 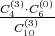 =
= 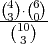 =
= 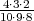 =
= 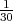 .
.
P(A) = 1 - P(Ac) = 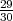 .
.
PRIMJER 4.5
U kutiji se nalazi 50 proizvoda: 20% neispravnih. Kontrolor izvlači 5 proizvoda
sukcesivno (bez vraćanja). Kolika je vjerojatnost da će ocjena kontrolora biti
pozitivna (svi proizvodi u uzorku ispravni)?
Rješenje: A=”izvučeni svi ispravni predmeti”,
A1=”prvi izvučeni ispravan”, P(A1) = 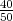
A2=”drugi izvučeni ispravan”, P(A2∕A1) = 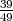 ,
,
A3=”treći izvučeni ispravan”, P(A3∕A1 ∩ A2) = 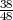 .
.
A4=”četvrti izvučeni ispravan”, P(A4∕A1 ∩ A2 ∩ A3) = 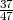 ,
,
A5=”peti izvučeni ispravan”, P(A5∕A1 ∩ A2 ∩ A3 ∩ A4) = 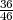
Prema formuli produkta (presjeka) vjerojatnosti
Ili direktno (pomoću formule za uzorak bez vraćanja):
Definicija 4.2 (NEZAVISNI DOGAĐAJI)
Neka je (Ω, ,P) vjerojatnosni prostor i neka su A,B ∈
,P) vjerojatnosni prostor i neka su A,B ∈ . Za dogadaje A i
B kažemo da su nezavisni ako vrijedi
. Za dogadaje A i
B kažemo da su nezavisni ako vrijedi
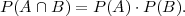
Definicija 4.3 (FAMILIJA NEZAVISNIH DOGAĐAJA)
Neka je (Ω, ,P) vjerojatnosni prostor i neka je Ai ∈
,P) vjerojatnosni prostor i neka je Ai ∈  ,i ∈ I familija
dogadaja. Kažemo da je to nezavisna familija dogadaja ako za svaki konačni
podskup različitih indeksa {i1,...,ik}∈ I vrijedi
,i ∈ I familija
dogadaja. Kažemo da je to nezavisna familija dogadaja ako za svaki konačni
podskup različitih indeksa {i1,...,ik}∈ I vrijedi
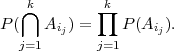
PRIMJER 4.6 Ako su A i B nezavisni dogadaji, takvi da P(A) > 0, P(B) > 0
onda vrijedi

PRIMJER 4.7
(a) Proizvoljan dogadaj A i siguran dogadaj su nezavisni.
(b) Proizvoljan dogadaj A i nemoguć dogadaj uvijek su nezavisni.
Rješenje:
(a) Ω ∩ A = A, P(Ω) = 1, P(Ω ∩ A) = P(A) = P(A) ⋅ 1 = P(A) ⋅ P(Ω).
(b) ∅∩ A = ∅, P(∅) = 0, P(∅∩ A) = P(∅) = P(∅) ⋅ P(A) = 0.
PRIMJER 4.8 Ako su A i B nezavisni dogadaji onda su nezavisni dogadaji:
(a) Ac i B,
(b) A i Bc,
(c) Ac i Bc.
Rješenje:
(a) (Ac ∩ B) ∩ (A ∩ B) = ∅, (Ac ∩ B) ∪ (A ∩ B) = B
⇒ P(B) = P(Ac ∩ B) + P(A ∩ B)
(b) (A ∩ Bc) ∩ (A ∩ B) = ∅, (A ∩ Bc) ∪ (A ∩ B) = A,
⇒ P(A) = P(A ∩ Bc) + P(A ∩ B),
(c) (Ac ∩ Bc) = (A ∪ B)c,
PRIMJER 4.9
Motor pokreće električni generator. Vjerojatnost otkazivanja motora u roku
jednog mjeseca je 0.08, a generatora 0.04. Kolika je vjerojatnost da ćemo morati
popravljati cijeli uredaj tijekom tog mjeseca?
Rješenje: Prema svojstvu (e) vjerojatnosti A,B ∈ ⇒ P(A∪B) = P(A) + P(B) -P(A∩B)
za dogadaj A =pokvario se motor i dogadaj B = pokvario se generator,
računamo vjerojatnost P(A ∪ B). Budući su dogadaji A i B nezavisni onda
je P(A ∩ B) = P(A) ⋅ P(B). Vjerojatnost otkazivanja cijelog uredaja je
P(A ∪ B) = 0.08 + 0.04 - 0.08 ⋅ 0.04 = 0.1168. Vjerojatnost da će trebati popravak je
11.68
⇒ P(A∪B) = P(A) + P(B) -P(A∩B)
za dogadaj A =pokvario se motor i dogadaj B = pokvario se generator,
računamo vjerojatnost P(A ∪ B). Budući su dogadaji A i B nezavisni onda
je P(A ∩ B) = P(A) ⋅ P(B). Vjerojatnost otkazivanja cijelog uredaja je
P(A ∪ B) = 0.08 + 0.04 - 0.08 ⋅ 0.04 = 0.1168. Vjerojatnost da će trebati popravak je
11.68
PRIMJER 4.10 Ako su A i B nezavisni dogadaji pozitivnih vjerojatnosti onda
se dogadaji ne isključuju.
Rješenje: Pretpostavimo suprotno: A ∩ B = ∅.
A i B su nezavisni i pozitivnih vjerojatnosti ⇒ P(A∩B) = P(A) ⋅P(B) > 0, što je u
kontradikciji s P(A ∩ B) = P(∅) = 0.
Zaključujemo da je pretpostavka kriva: ⇒ A ∩ B≠∅, dogadaji se ne isključuju.
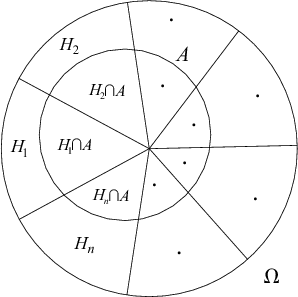
TEOREM 4.4 (FORMULA POTPUNE VJEROJATNOSTI)
Neka je (Ω, ,P) vjerojatnosni prostor i neka skupovi H1,H2,...,Hn ∈
,P) vjerojatnosni prostor i neka skupovi H1,H2,...,Hn ∈ čine
potpun sistem dogadaja. Tada
čine
potpun sistem dogadaja. Tada
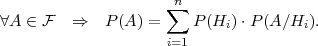
Dokaz:
Skupovi H1,H2,...,Hn ∈ , čine potpun sistem (familiju) dogadaja:
, čine potpun sistem (familiju) dogadaja:
Hi ∩ Hj = ∅, i≠j, ⋃
i=1nHi = Ω, ∑
i=1nP(Hi) = 1.
Prema teoremu o vjerojatnosti produkta (presjeka) dogadaja:
P(A ∩ Hi) = P(Hi) ⋅ P(A∕Hi).
A ∈ , (A ∩ Hi) ∩ (A ∩ Hj) = ∅.
, (A ∩ Hi) ∩ (A ∩ Hj) = ∅.
tko želi znati više
TEOREM 4.5 (FORMULA POTPUNE VJEROJATNOSTI ZA UVJETNU
VJEROJATNOST)
Neka je (Ω, ,P) vjerojatnosni prostor i neka skupovi H1,H2,...,Hn ∈
,P) vjerojatnosni prostor i neka skupovi H1,H2,...,Hn ∈ čine
potpun sistem dogadaja. Tada
čine
potpun sistem dogadaja. Tada
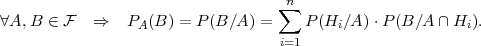
Dokaz:
Prema formuli potpune vjerojatnosti za uvjetnu vjerojatnost i definiciji uvjetne
vjerojatnosti vrijedi:
TEOREM 4.6 (BAYESOVA FORMULA)
Neka je (Ω, ,P) vjerojatnosni prostor i neka skupovi H1,H2,...,Hn ∈
,P) vjerojatnosni prostor i neka skupovi H1,H2,...,Hn ∈ čine
potpun sistem dogadaja. Neka dogadaj A ∈
čine
potpun sistem dogadaja. Neka dogadaj A ∈ ima pozitivnu vjerojatnost P(A) > 0.
Tada je ∀i
ima pozitivnu vjerojatnost P(A) > 0.
Tada je ∀i
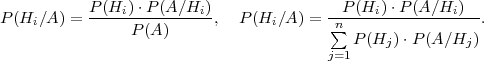
Dokaz:
Definicija uvjetne vjerojatnosti i formula produkta vjerojatnosti povlači da
vrijedi:
P(Hi∕A) = 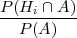 =
= 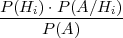 .
.
Prema formuli potpune vjerojatnosti dobivamo:
P(Hi∕A) = 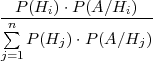 .
.
NAPOMENA 4.2
Bayesovu formulu koristimo kad želimo naći istinitu hipotezu iz skupa od n
postavljenih hipoteza Hi,i = 1,...,n, ako znamo da se dogodio dogadaj A. Za svako
i = 1,...,n, računamo P(Hi∕A). Hipoteza Hi0 za koju je P(Hi0∕A) ≈ 1, uzima se
da je ispravna.
PRIMJER 4.11 Na našem fakultetu je 4% studenata i 1% studentica koji nisu
državljani RH. Omjer studenata i studentica upisanih na fakultet je 40:60. Ako je
slučajno izabrana jedna osoba upisana na naš fakultet koja je strani državljanin
kolika je vjerojatnost da je to studentica?
Rješenje:
Postavljamo hipoteze-potpun sistem dogadaja:
H1 =”izabrana osoba je studentica”, P(H1) = 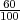 .
.
H2 =”izabrana osoba je student”, P(H2) = 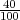 .
.
H1 ∩ H2 = ∅, H1 ∪ H2 = Ω.
Dogadaj A koji se dogodio: A=”izabrana osoba je strani državljanin”.
Zadane su uvjetne vjerojatnosti dogadaja A uz uvjet jedne i druge hipoteze:
P(A∕H1) = 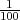 , P(A∕H2) =
, P(A∕H2) = 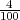 . Trebamo odrediti P(H1∕A) =?
. Trebamo odrediti P(H1∕A) =?
Koristimo Bayesovu formulu:
PRIMJER 4.12
Tri stroja S1, S2 i S3 učestvuju u ukupnoj proizvodnji u omjeru 60 : 30 : 10.
Stroj S1 proizvodi 2%, stroj S2 3% i stroj S3 4% neispravnih proizvoda. Ako se
slučajno izabere jedan proizvod koji je neispravan, kolika je vjerojatnost da je bio
napravljen na stroju S3?
Rješenje:
Postavljamo hipoteze-potpun sistem dogadaja:
H1 =”izabrani predmet je sa stroja S1”, P(H1) = 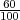 .
.
H2 =”izabrani predmet je sa stroja S2”, P(H2) = 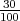 .
.
H3 =”izabrani predmet je sa stroja S3”, P(H3) = 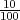
Hi ∩ Hj = ∅,i≠j, H1 ∪ H2 ∪ H3 = Ω.
Dogadaj A koji se dogodio: A=”izabrani proizvod je neispravan”.
Zadane su uvjetne vjerojatnosti dogadaja A uz uvjet pojedine hipoteze:
P(A∕H1) = 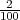 , P(A∕H2) =
, P(A∕H2) = 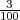 , P(A∕H3) =
, P(A∕H3) = 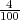 .
.
Trbamo odrediti P(H3∕A) =?
Koristimo Bayesovu formulu:
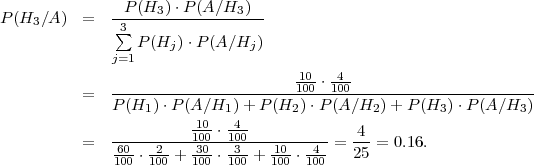
PRIMJER 4.13 motiv
Kontolor u tvornici daje nakon vizualnog pregleda tri tipa odluke: 1) proizvod
je defektan i šalje se na daljnje pretrage 2) sumnja se da je proizvod defektan
i šalje se na daljnje pretrage 3) proizvod je ispravan. Pokazalo se dosada da je
kontolor bio u pravu kad je odlučio: o neispravnosti u 80% slučajeva, o sumnji na
neispravnost u 50% slučajeva, a o ispravnosti proizvoda a u 90% slučajeva.
U toku jednog dana kontrolor donosi prvu odluku kod 50%, drugu kod 20%
i treću dijagnozu kod 30% proizvoda. (a) Odredite vjerojatnost neispravnosti
proizvoda. (b) Odredite vjerojatnost pogrešne odluke tj. odluke kontolora da je
proizvod ispravan a on je zaista neispravan. (c) Odredite vjerojatnost nepotrebnih
troškova ili slanja na daljnje pretrage proizvoda ako je zaista ispravan.
Rješenje:
Postavljamo hipoteze-potpun sistem dogadaja:
H1 =”prva odluka -proizvod je neispravan”, P(H1) = 0.5;
H2 =”druga odluka - sumnja se da je proizvod neispravan ”, P(H2) = 0.2;
H3 =”treća odluka- proizvod je ispravan”, P(H3) = 0.3.
Hi ∩ Hj = ∅,i≠j, H1 ∪ H2 ∪ H3 = Ω.
Dogadaj A = ”proizvod je neispravan”.
Dogadaj Ac =”proizvod je ispravan”.
Zadane su uvjetne vjerojatnosti dogadaja A uz uvjet pojedine hipoteze:
P(A∕H1) = 0.8, P(A∕H2) = 0.5 P(A∕H3) = 0.1.
(a) Trebamo odrediti P(A)
(b) Trbamo odrediti P(H3∕A) =?
(c) Trebamo odrediti P(H1 ∪ H2∕Ac)
(a) Koristimo formulu potpune vjerojatnosti:
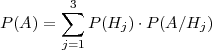
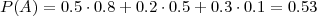
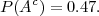 (b)Koristimo Bayesovu formulu:
(b)Koristimo Bayesovu formulu:
(c) Koristimo Bayesovu formulu:
4.1 Ponovimo
UVJETNA VJEROJATNOST
|
|
| Uvjetna vjerojatnost od B uz uvjet da se dogodio A | PA(B) ≡ P(B∕A) |
|
|
| ako P(A) > 0 | PA(B) = 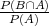 |
|
|
| ako P(A) = 0 | PA(B) = P(B) |
|
|
| formula produkta vjerojatnosti | P(A ∩ B) = P(A) ⋅ PA(B) |
|
|
| nezavisni dogadaji A i B | P(A ∩ B) = P(A) ⋅ P(B) |
|
|
| formula potpune vjerojatnosti | P(A) = ∑
j=1nP(Hj) ⋅ P(A∕Hj) |
|
|
| Bayesova formula | P(Hi∕A) = 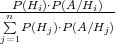 |
|
|
| |
 ,P) vjerojatnosni prostor i neka je A ∈
,P) vjerojatnosni prostor i neka je A ∈ takav da je P(A) > 0. Tada
funkciju PA :
takav da je P(A) > 0. Tada
funkciju PA :  → [0,1] zovemo uvjetna vjerojatnost a definiramo ∀ B ∈
→ [0,1] zovemo uvjetna vjerojatnost a definiramo ∀ B ∈ kao
kao