1. Pravac je okomit na ravninu ako je okomit na bilo koja dva neparalelna pravca te ravnine.
2. Svakom točkom ravnine moguće je položiti samo jedan pravac okomit na tu ravninu.
3. Ako su dva pravca okomita na istu ravninu, onda su oni međusobno paralelni.
4. Ako je pravac okomit na dvije ravnine, onda su one paralelne.
5. Ako je pravac okomit na ravninu α, onda je svaka ravnina β koja sadrži taj pravac okomita na α.
6. Ako je ravnina γ okomita na presječnicu p ravnina α i β, onda je ona okomita i na α i na β.

• Neka je dana ravnina α ( r₁, r₂).
  Tlocrt normale n ravnine α okomit je na prvi trag ravnine, a nacrt normale n okomit je na drugi trag, odnosno n' ⊥ r₁ i n'' ⊥ r₂.

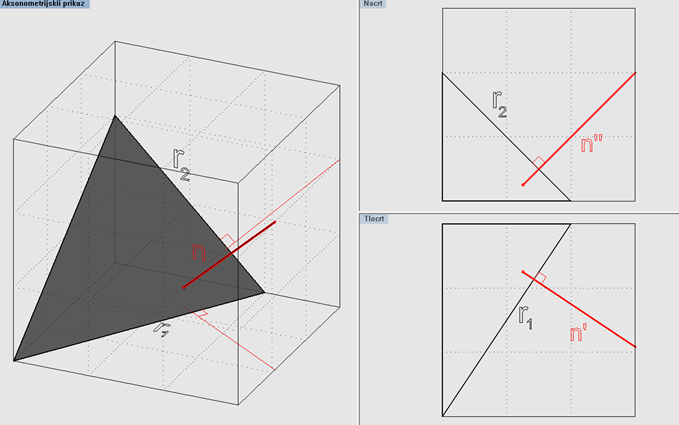
Slika 5.1 Normala n(n', n'') ravnine α ( r1, r2)

Riješeni primjeri:

1. Dan je pravac p(p', p'').
   Problem: Postaviti bilo koji pravac q okomit na dani pravac p. (Slika )
   
   Pravac okomit na zadni pravac dobit ćemo ako tim pravcem položimo bilo koju ravninu okomitu na zadani pravac. Svaki pravac ove ravnine okomit je na zadani pravac.
   

   Slika 5.2

   Slika 5.3

   Rješenje:
   • Odaberimo proizvoljnu točku T pravca p i postavimo ravinu kroz T okomito na pravac p.
   • Odabrali smo pravac q određen probodištima Q₁ i Q₂.
   
   
   
2. Dana je ravnina α( r₁, r₂).
   Problem: Postaviti bilo koju ravninu β okomitu na zadanu ravninu α.


Ravninu okomitu na neku zadanu ravninu dobit ćemo ako na danu ravninu postavimo okomit pravac. Svaka ravnina koja sadrži ovaj pravac okomita je na zadanu ravninu.



Slika 5.4

Slika 5.5

Rješenje:
• Odabrali smo po volji točku T u ravnini α i kroz nju smo postavili smo pravac p okomito na α.
• Probodišta P₁ i P₂ pravca p leže na odgovarajućim tragovima ravnine β.


3. Dana je dužina AB [A(A', A''), B(B', B'')] i ravnina α( r₁, r₂).
   Problem: Odredite pravac q u ravnini α čija je svaka točka jednako udaljena od točaka A i B. (Slika )
   

   Slika 5.6

   Slika 5.6

   Rješenje:
   • Skup svih točaka u prostoru koje su jednako udaljene od danih dviju točaka A i B je simetralna ravnina dužine AB.
     Simetralna ravnina neke dužine je ravnina koja tu dužinu raspolavlja i okomita je na nju.
   • Traženi pravac mora ležati u simetralnoj ravnini dužine AB i u zadanoj ravnini α pa ga određujemo kao njihovu presječnicu. (vidi Presječnica)



4. Ortogonalna projekcija objekata na po volji zadanu ravninu
   
   
   1. Dana je točka T(T', T'') i ravnina α ( r₁, r₂).
      Problem: Odrediti (ortogonalnu) projekciju točke T na ravninu α.
      
      

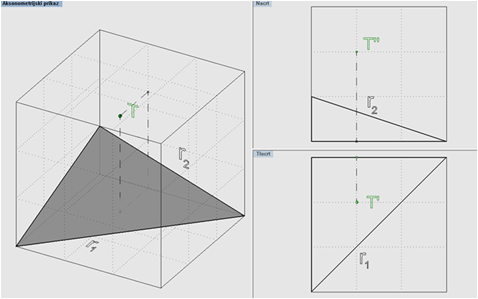
      Slika 5.7

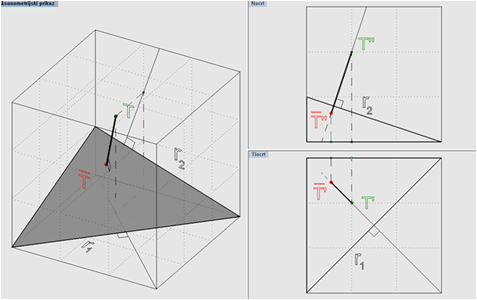
      Slika 5.8

      Rješenje:
      • Ako T ne leži u ravnini α, možemo povući okomicu o iz točke T na danu ravninu α.
      • Probodište okomice i ravnine α, točka T, odredit će traženu ortogonalnu projekciju točke na ravninu. (vidi Probodište)
      • Uočimo, kad bi točka T ležala u ravnini α , njezina ortogonalna projekcija na α podudarala bi se s danom točkom T.
   
   
   
   2. Dan je pravac m(m', m'') i ravnina α ( r₁, r₂). (slika 5.9)
      Problem: Odrediti (ortogonalnu) projekciju pravca m na ravninu α.
      
      

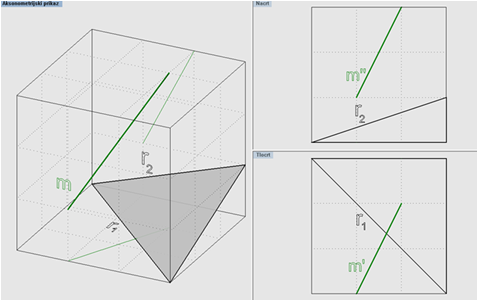
      Slika 5.9

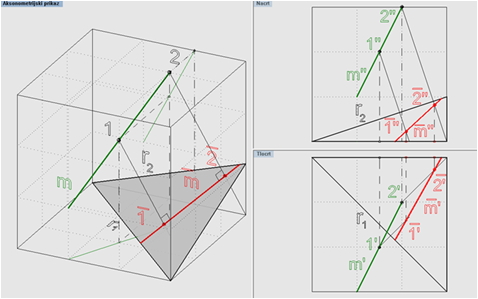
      Slika 5.10

      Rješenje:
      • Ortogonalno projiciranje čuva incidenciju pa je ortogonalna projekcija pravca na danu ravninu određena kao spojnica ortogonalnih projekcija dviju po volji odabranih točaka pravca na tu ravninu.
      • Na slici 5.10 odabrane su točke 1 i 2 na pravcu m i određene su njihove ortogonalne projekcije 1POTEZ, 2 POTEZ. Tražena projekcija je pravac m POTEZ.
      • Općenito, kao jednu od točaka na pravcu kojeg projiciramo možemo odabrati točku probodišta pravca s ravninom β. Ova točka projicirat će se sama u sebe.