Intersections of cones, cylinders and spheres



Intersections of the following types of surfaces - cones or cylinders of the 2nd order or spheres are algebraic space curves of the 4th order.

There are two types of algebraic space curves of the 4th order (type I and type II). The curves of the type I are intersection curves of two quadric surfaces. The curves of the type II are curves in the decomposition of curves of the 6th order that are intersections of a ruled surface of 3rd order and a ruled surface of 2nd order that have one common line and that line is a double line of the surface of the 3rd order.

We will only work with space curves of type I that are intersections of cones, cylinders and spheres.

Those curves can have at most one double point if they are proper.

There are 3 types of proper space curves of the 4th order and type I:
  • one-branch,
  • two-branch and
  • space curves of the 4th order with one double point.

    There are 4 possible decompositions of space curves of the 4th order:
  • curve of the 3rd order and a line,
  • 2 curves of the 2nd order,
  • curve of the 2nd order and 2 lines,
  • 4 lines.

    EXAMPLES OF PROPER SPACE CURVES OF THE 4th ORDER

    File where you can rotate the figures using your mouse.
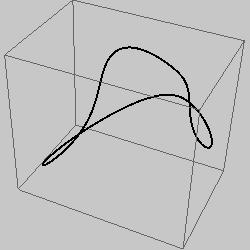    one-branch
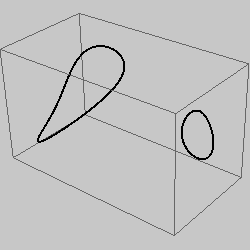
    two-branch
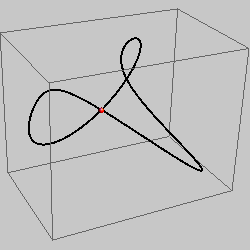
    with a double point


    EXAMPLES OF DECOMPOSITIONS OF A SPACE CURVE OF THE 4th ORDER


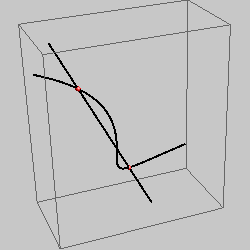    curve of the 3rd order and a line
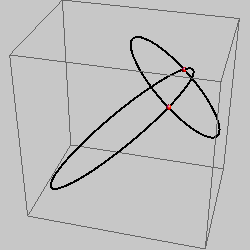
    two curves of the 2nd order
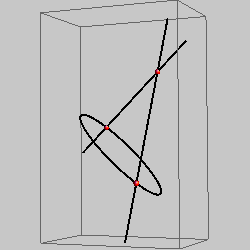
    curve of the 2nd order and two lines
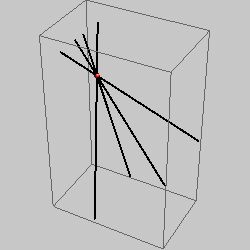
    four lines\(^*\)


    Order of a space curve is invariant under projection - the projection of a space curve of the order \(n\) is a plane curve of the same order. The reason why this is true is as follows: a line in the plane of projection is a projection of a projecting plane.
    Every plane in the space intersects a space curve of the \(n\)th order in \(n\) points, therefore, any line in the projection plane intersects the projection of the curve in \(n\) points. In other words, the projection of a space curve is a plane curve of the \(n\)th order.
    Since a plane curve can have more double points than a space curve to remain proper (can you remember that number?), the projection of a space curve is a plane curve with possibly more double points.

  • Rotate the figures above and observe how the projection of the curves changes. Try to find the position when the projection curve has one, two, three double points or a triple point.

    \(^*\) The point which is the intersection of the four lines is a fourfold point of the degenerated intersection curve of the 4th order. This point counts as 6 double points. There are different types of degeneration of a space curve of order 4 into 4 lines but we will only encounter this type of degeneration. In some examples, this fourfold point will be a point at infinity.

    INTERSECTION OF TWO CONES

    INTERSECTION OF A CONE AND A CYLINDER

    INTERSECTION OF TWO CYLINDERS

    INTERSECTION WITH A SPHERE






    Created by Sonja Gorjanc, translated by Helena Halas and Iva Kodrnja - 3DGeomTeh - Developing project of the University of Zagreb