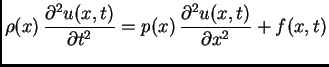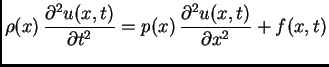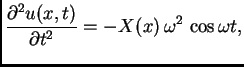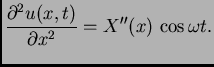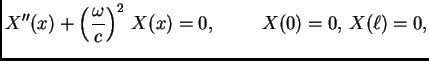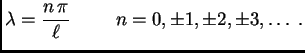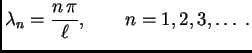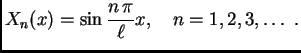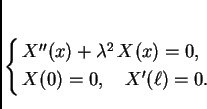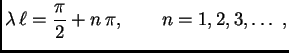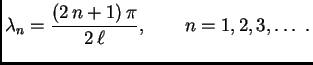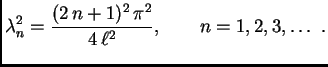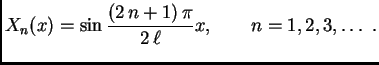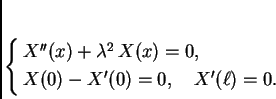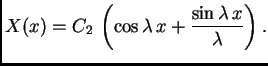Primjer 2.10
Naći vlastite vrijednosti i vlastite funkcije rubnog problema
Rješenje. Kao u (2.19) opće rješenje jednadžbe je
Iz
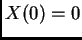
slijedi
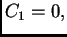
pa je
Iz
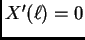
slijedi
Odatle
pa je
Tako su vlastite vrijednosti
Vlastite funkcije su
Primjer 2.11
Naći vlastite vrijednosti i vlastite funkcije rubnog problema
Rješenje. Opće rješenje jednadžbe je
Iz
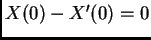
slijedi
Iz
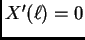
slijedi
odnosno
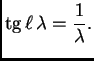 |
(2.19) |
To je transcendentna (nije algebarska) jednadžba. Takve se jednadžbe
u pravilu ne mogu elementarno rješavati, i gotovo uvijek se moramo
zadovoljiti s približnim rješenjem. O približnom rješavanju
jednadžbi bit će riječi u trećem poglavlju
3.2. Ovdje
napomenimo samo toliko da su za
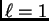
prva tri rješenja približno
Slika:
Rješenja jednadžbe
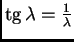
|
|
Tako su prve tri vlastite funkcije približno jednake
Slika 2.7:
Vlastite funkcije
|
|