Next: Konvergencija.
Up: Fourierova metoda
Previous: Vlastite funkcije i vlastite
Sadržaj
Indeks
Fourierovi redovi
Rješavajući valnu jednadžbu, uvaživši rubne uvjete, dobili smo
rješenja oblika
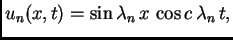
ili
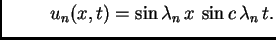
Problem oscilacija žice je
potpuno zadan tek kad zadamo još i početne uvjete. Na pr.
Općenito niti jedna od
funkcija 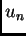 ne zadovoljava početne uvjete. Zato rješenje tražimo
u obliku linearne kombinacije. Funkcije su linearno nezavisne, i
ima ih beskonačno mnogo, pa linearna kombinacija postaje
beskonačni red
ne zadovoljava početne uvjete. Zato rješenje tražimo
u obliku linearne kombinacije. Funkcije su linearno nezavisne, i
ima ih beskonačno mnogo, pa linearna kombinacija postaje
beskonačni red
Ako je 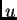 rješenje koje zadovoljava početne uvjete, onda mora biti
Da li postoje takvi
rješenje koje zadovoljava početne uvjete, onda mora biti
Da li postoje takvi 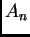 da vrijedi ova jednakost? Za kakve funkcije
postoje
da vrijedi ova jednakost? Za kakve funkcije
postoje 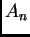 takvi da vrijedi ova jednakost? Ovakva pitanja i još
mnoga druga dovode nas do pojma Fourierovih redova.
takvi da vrijedi ova jednakost? Ovakva pitanja i još
mnoga druga dovode nas do pojma Fourierovih redova.
Funkcije
su periodične, i period je broj 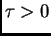 takav da vrijedi
Odatle slijedi
takav da vrijedi
Odatle slijedi
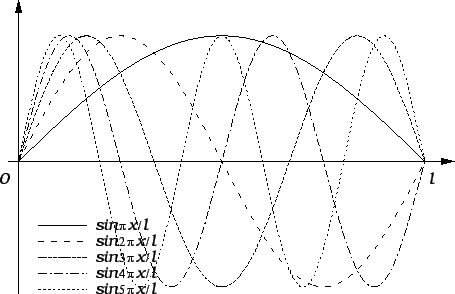
Svaka od ovih funkcija ima period 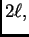 jer je višekratnik perioda
također period, pa se nadamo da pomoću
njih možemo prikazati svaku periodičku funkciju
jer je višekratnik perioda
također period, pa se nadamo da pomoću
njih možemo prikazati svaku periodičku funkciju 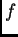 perioda
perioda 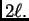 No, pomoću njih se mogu prikazati samo neparne funkcije, jer je
sinus neparna funkcija.
No, pomoću njih se mogu prikazati samo neparne funkcije, jer je
sinus neparna funkcija.
To ograničenje izbjegavamo tako da dodamo i odgovarajuće kosinusne
funkcije. Tako funkciju 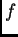 nastojimo napisati u obliku
nastojimo napisati u obliku
tj.
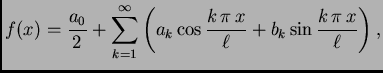 |
(2.20) |
gdje su koeficijenti 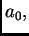
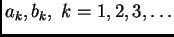 neodređeni. Da bismo koeficijente odredili tako da
vrijedi ova jednakost, koristimo jedno važno svojstvo
trigonometrijskih funkcija
Svojstvo izraženo formulama, u kojima je desna
strana jednaka nuli, se zove
ortogonalnost
trigonometrijskih funkcija, a formule se zovu
formule ortogonalnosti.
neodređeni. Da bismo koeficijente odredili tako da
vrijedi ova jednakost, koristimo jedno važno svojstvo
trigonometrijskih funkcija
Svojstvo izraženo formulama, u kojima je desna
strana jednaka nuli, se zove
ortogonalnost
trigonometrijskih funkcija, a formule se zovu
formule ortogonalnosti.
Sada računamo koeficijente tako da (2.21)
integriramo po segmentu duljine perioda (ovdje je to
![$ [-\ell,\ell]$](img1567.png) ), množimo redom s
), množimo redom s
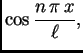
i
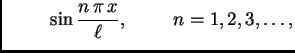
i zatim
integriramo po istom segmentu. Zbog svojstva ortogonalnosti
dobivamo
Da bi ove formule imale smisla, nužno je da 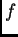 bude integrabilna
funkcija na segmentu
bude integrabilna
funkcija na segmentu
![$ [-\ell,\ell].$](img1572.png) U tom slučaju su koeficijenti
U tom slučaju su koeficijenti
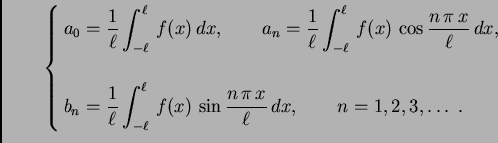 |
(2.21) |
Red oblika
se zove
trigonometrijski red, a brojevi

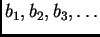 se zovu koeficijenti trigonometrijskog
reda. Trigonometrijski red
je dan čim su dani njegovi
koeficijenti. No, ako su koeficijenti trigonometrijskog reda dani
formulama (2.22), onda se red zove Fourierov red
funkcije
se zovu koeficijenti trigonometrijskog
reda. Trigonometrijski red
je dan čim su dani njegovi
koeficijenti. No, ako su koeficijenti trigonometrijskog reda dani
formulama (2.22), onda se red zove Fourierov red
funkcije 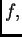 a koeficijenti se zovu
Fourierovi koeficijenti.
a koeficijenti se zovu
Fourierovi koeficijenti.
Do sada smo stalno imali na umu periodičku funkciju 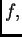 perioda
perioda
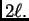 Pretpostavimo da je funkcija
Pretpostavimo da je funkcija 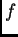 definirana na skupu koji
sadrži
definirana na skupu koji
sadrži
![$ [-\ell,\ell],$](img1578.png) da je integrabilna na
da je integrabilna na
![$ [-\ell,\ell],$](img1578.png) i da
nije periodička. U tom slučaju također možemo izračunati
Fourierove koeficijente i prema tome imamo Fourierov red. Budući da
svaka funkcija u tom redu ima period
i da
nije periodička. U tom slučaju također možemo izračunati
Fourierove koeficijente i prema tome imamo Fourierov red. Budući da
svaka funkcija u tom redu ima period 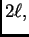 i red će predstavljati
periodičku funkciju perioda
i red će predstavljati
periodičku funkciju perioda 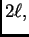 i to onu koja se iz dane dobije
periodičkim proširenjem njezine restrikcije na segmentu
i to onu koja se iz dane dobije
periodičkim proširenjem njezine restrikcije na segmentu
![$ [-\ell,\ell]$](img1567.png) na cijeli
na cijeli
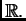 Reći ćemo da je to red funkcije
Reći ćemo da je to red funkcije 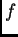 na
na
![$ [-\ell,\ell].$](img1572.png)
Subsections





Next: Konvergencija.
Up: Fourierova metoda
Previous: Vlastite funkcije i vlastite
Sadržaj
Indeks
2001-10-26
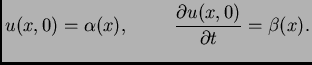
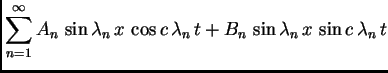
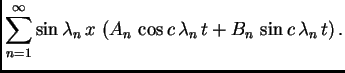
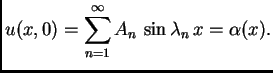
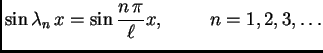
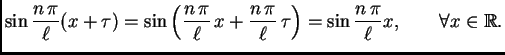
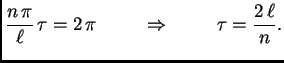
![]() jer je višekratnik perioda
također period, pa se nadamo da pomoću
njih možemo prikazati svaku periodičku funkciju
jer je višekratnik perioda
također period, pa se nadamo da pomoću
njih možemo prikazati svaku periodičku funkciju ![]() perioda
perioda ![]() No, pomoću njih se mogu prikazati samo neparne funkcije, jer je
sinus neparna funkcija.
No, pomoću njih se mogu prikazati samo neparne funkcije, jer je
sinus neparna funkcija.
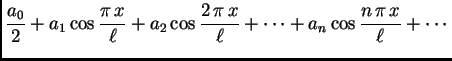
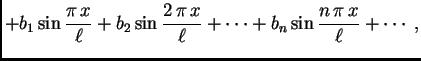
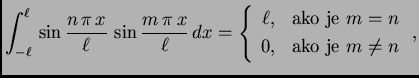
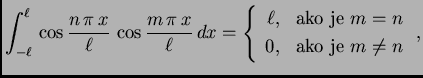
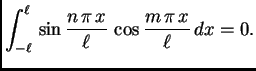
![]() ), množimo redom s
), množimo redom s
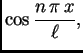 i
i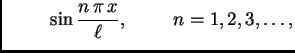
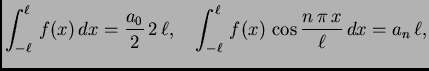
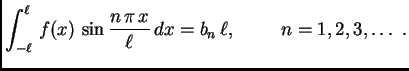
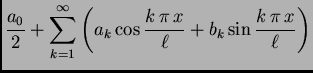
![]() perioda
perioda
![]() Pretpostavimo da je funkcija
Pretpostavimo da je funkcija ![]() definirana na skupu koji
sadrži
definirana na skupu koji
sadrži
![]() da je integrabilna na
da je integrabilna na
![]() i da
nije periodička. U tom slučaju također možemo izračunati
Fourierove koeficijente i prema tome imamo Fourierov red. Budući da
svaka funkcija u tom redu ima period
i da
nije periodička. U tom slučaju također možemo izračunati
Fourierove koeficijente i prema tome imamo Fourierov red. Budući da
svaka funkcija u tom redu ima period ![]() i red će predstavljati
periodičku funkciju perioda
i red će predstavljati
periodičku funkciju perioda ![]() i to onu koja se iz dane dobije
periodičkim proširenjem njezine restrikcije na segmentu
i to onu koja se iz dane dobije
periodičkim proširenjem njezine restrikcije na segmentu
![]() na cijeli
na cijeli
![]() Reći ćemo da je to red funkcije
Reći ćemo da je to red funkcije ![]() na
na
![]()