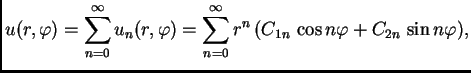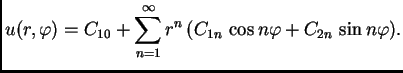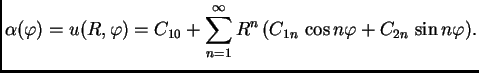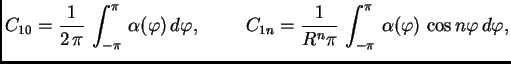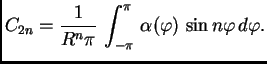Next: Beskonačna membrana s rupom
Up: Metoda separacije varijabli (Fourierova
Previous: Metoda separacije varijabli (Fourierova
Sadržaj
Indeks
Dirichletov problem za ravnotežu kružne membrane
Dirichletov problem za ravnotežu kružne membrane glasi
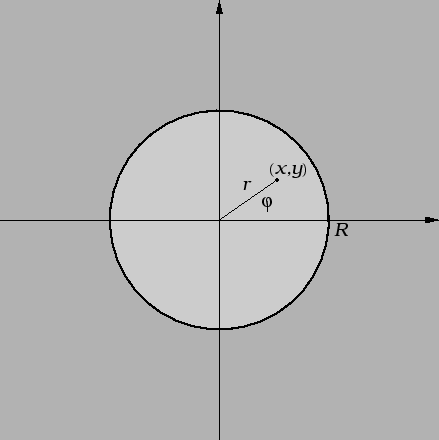
gdje 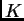 označava krug radiusa
označava krug radiusa 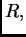 a
a
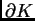 njegov rub,
kružnicu radiusa
njegov rub,
kružnicu radiusa 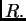 Prirodno je koordinatni sustav izabrati
sukladno geometrijskim karakteristikama područja. Zato u ovom
slučaju koristimo polarni koordinatni sustav u ravnini, i to tako da
ishodište stavimo u središte kruga.
Prirodno je koordinatni sustav izabrati
sukladno geometrijskim karakteristikama područja. Zato u ovom
slučaju koristimo polarni koordinatni sustav u ravnini, i to tako da
ishodište stavimo u središte kruga.
U polarnom koordinatnom sustavu su koordinate 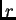 i
i 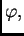
pa je
Postavlja se pitanje u što se transformira
kad se pređe na funkciju
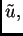 tj. kad se
Laplace računa u polarnom sustavu u ravnini. To je riješeno kao
jedan od primjera za deriviranje kompozicije funkcija (lančano
pravilo) u predavanjima iz Matematike
2.
tj. kad se
Laplace računa u polarnom sustavu u ravnini. To je riješeno kao
jedan od primjera za deriviranje kompozicije funkcija (lančano
pravilo) u predavanjima iz Matematike
2.
![[*]](file:/usr/share/latex2html/icons/crossref.png) . Tamo vidimo da je
U daljnjem ćemo umjesto
. Tamo vidimo da je
U daljnjem ćemo umjesto 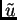 pisati radije
pisati radije 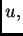 pa jednadžba
prema tome glasi
pa jednadžba
prema tome glasi
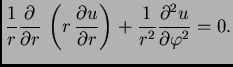 |
(2.52) |
Budući da smo ishodište polarnog koordinatnog sustava postavili u
središte kruga, čiji je radius 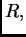 rubni uvjet se može zapisati
ovako
rubni uvjet se može zapisati
ovako
Rješenje tražimo u obliku
Uvrstimo u jednadžbu (2.54), dobivamo
Podijelimo s 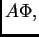 i pomnožimo s
i pomnožimo s 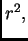 pa imamo
gdje je
pa imamo
gdje je 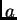 konstanta, jer smo separirali varijable. Imamo
Budući da je
konstanta, jer smo separirali varijable. Imamo
Budući da je 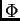 periodička funkcija (zbog geometrije problema),
periodička funkcija (zbog geometrije problema), 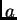 mora biti pozitivan, na pr.
mora biti pozitivan, na pr.
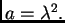 Slijedi
Opće rješenje druge jednadžbe je
Period funkcije
Slijedi
Opće rješenje druge jednadžbe je
Period funkcije 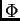 je
je 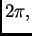 pa slijedi
Za drugu jednadžbu imamo dakle ova rješenja
Prva jednadžba sada glasi
pa slijedi
Za drugu jednadžbu imamo dakle ova rješenja
Prva jednadžba sada glasi
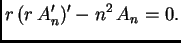 |
(2.53) |
Za 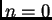 imamo
što nakon dijeljenja s
imamo
što nakon dijeljenja s 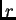 postaje
U slučaju
postaje
U slučaju 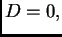 imamo
Ako je
imamo
Ako je 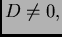 onda nakon još jednog dijeljenja s
onda nakon još jednog dijeljenja s 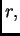 i
integriranja, dobivamo
pa je u tom slučaju opće rješenje
Rješenja za
i
integriranja, dobivamo
pa je u tom slučaju opće rješenje
Rješenja za 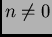 potražimo u obliku
Lako se vidi da je
Prema tome jednadžba (2.55) se svodi na
odakle
pa su tako rješenja jednadžbe (2.55) za
potražimo u obliku
Lako se vidi da je
Prema tome jednadžba (2.55) se svodi na
odakle
pa su tako rješenja jednadžbe (2.55) za 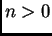 Opće rješenje za
Opće rješenje za 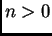 je
Budući da se radi o krugu, za koji je
je
Budući da se radi o krugu, za koji je
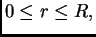 rješenja
rješenja 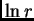 za
za 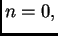 i
i
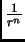 ne dolaze u obzir, jer te funkcije
nisu definirane za
ne dolaze u obzir, jer te funkcije
nisu definirane za 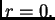 Tako imamo rješenja
Tako imamo rješenja
Sve ovo smo dobili direktno iz jednadžbe uz uvažavanje određenih
fizikalnih činjenica. Iskoristimo sada rubni uvjet. Nijedno od
rješenja 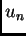 ne mora zadovoljavati rubni uvjet. Zato pretpostavimo
rješenje rubnog problema u obliku
ne mora zadovoljavati rubni uvjet. Zato pretpostavimo
rješenje rubnog problema u obliku
što se može napisati ovako
Ovo rješenje mora zadovoljavati rubni uvjet
To je Fourierov red funkcije 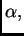 pa slijedi
pa slijedi
Subsections





Next: Beskonačna membrana s rupom
Up: Metoda separacije varijabli (Fourierova
Previous: Metoda separacije varijabli (Fourierova
Sadržaj
Indeks
2001-10-26


![]() i
i ![]()
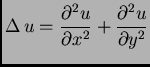
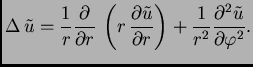
![]() rubni uvjet se može zapisati
ovako
rubni uvjet se može zapisati
ovako
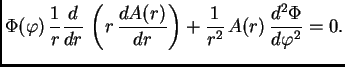
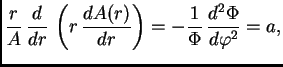
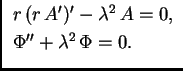
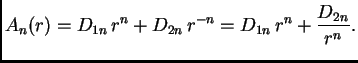
![]() ne mora zadovoljavati rubni uvjet. Zato pretpostavimo
rješenje rubnog problema u obliku
ne mora zadovoljavati rubni uvjet. Zato pretpostavimo
rješenje rubnog problema u obliku