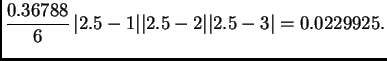Radi jednostavnosti pretpostavimo da je
Dokaz. Ako je ![]() za neki
za neki ![]() onda nemamo što dokazivati, jer su tada obje strane u
(3.15) jednake nuli. Zato pretpostavimo da je
onda nemamo što dokazivati, jer su tada obje strane u
(3.15) jednake nuli. Zato pretpostavimo da je
![]() i
i
![]() za svaki
za svaki ![]() Stavimo, radi kraćeg
zapisa
Stavimo, radi kraćeg
zapisa
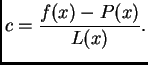
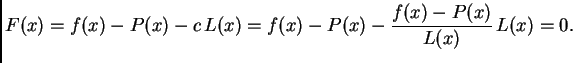
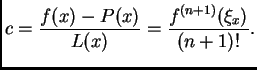
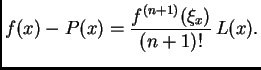
Iz ovog teorema proizlazi sljedeća ocjena greške. Neka je
Rješenje. Po formuli (3.14) imamo
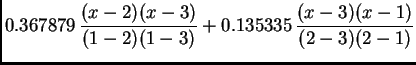 |
|||
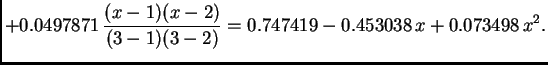 |