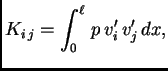
Metoda konačnih elemenata je modifikacija Ritzove metode u tom smislu da što više elemenata matrice krutosti bude jednako nuli. Budući da su elementi matrice krutosti
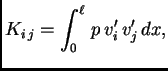
Pogledajmo na primjeru kako se to radi. Neka je dan rubni problem
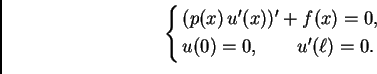
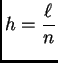
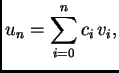
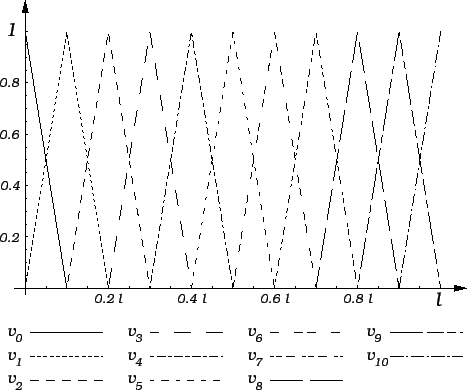
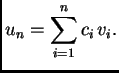
Iz formule (3.29) slijedi
![% latex2html id marker 41016
$\displaystyle v_i'(x) =
\begin{cases}
\frac{1}{h}...
... $x_i\leqslant{}x\leqslant{}x_{i+1}$} \\ [1mm]
0,& \text{inače}.
\end{cases}$](img3402.png)
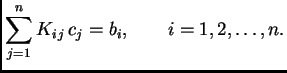
Rješenje. Budući da je uvjet na desnom rubu homogen i prirodan, njega ne
treba uzimati u obzir kod izbora koordinatnih funkcija. Uvjet na
lijevom rubu nam kaže da treba isključiti funkciju ![]() Dakle
rješenje treba tražiti kao
Dakle
rješenje treba tražiti kao