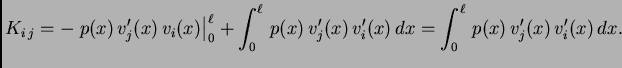Next: Parcijalne diferencijalne jednadžbe
Up: Rubni problem
Previous: Metoda konačnih elemenata
Sadržaj
Indeks
Galerkinova metoda
Galerkinova metoda ili preciznije metoda Bubnova-Galerkina osniva se
na sljedećoj jednostavnoj činjenici. Neka je dan vektorski prostor
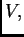 baza
baza
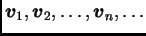 u
u 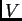 i skalarni produkt u
i skalarni produkt u 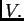 Tada je
Tada je
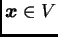 nulvektor, ako i samo ako je
nulvektor, ako i samo ako je
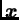 okomit na
okomit na
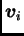 za svaki
za svaki 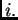 Ta tvrdnja je jasna, ako za
Ta tvrdnja je jasna, ako za 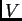 uzmemo vektorski prostor radijvektora u prostoru ili ravnini.
uzmemo vektorski prostor radijvektora u prostoru ili ravnini.
Ono što nas zanima je rubni problem, na pr.
Rješenje tražimo u skupu 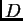 funkcija koje su klase
funkcija koje su klase
![$ C^2([0,\ell]),$](img3437.png) i koje
zadovoljavaju rubne uvjete. Taj skup nije vektorski prostor, jer
linearne kombinacije takvih funkcija više ne zadovoljavaju ove rubne
uvjete. Međutim, ako su rubni uvjeti homogeni, onda skup
i koje
zadovoljavaju rubne uvjete. Taj skup nije vektorski prostor, jer
linearne kombinacije takvih funkcija više ne zadovoljavaju ove rubne
uvjete. Međutim, ako su rubni uvjeti homogeni, onda skup 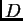 jeste vektorski prostor. Homogenizacijom rubnih uvjeta možemo
svaki rubni problem svesti na problem s homogenim
uvjetima.
jeste vektorski prostor. Homogenizacijom rubnih uvjeta možemo
svaki rubni problem svesti na problem s homogenim
uvjetima.
Promatrajmo dakle rubni problem
U skupu 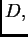 koji je sada vektorski prostor, definirajmo skalarni
produkt
Izaberimo u
koji je sada vektorski prostor, definirajmo skalarni
produkt
Izaberimo u 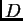 linearno nezavisne funkcije
tako da čine bazu u
linearno nezavisne funkcije
tako da čine bazu u 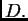 U pravilu funkcija
U pravilu funkcija 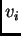 ima beskonačno
mnogo. Neka je
ima beskonačno
mnogo. Neka je 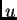 rješenje rubnog problema. Tada je
rješenje rubnog problema. Tada je 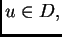 i
prema tome postoje brojevi
i
prema tome postoje brojevi
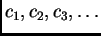 takvi da je
U diferencijalnoj
jednadžbi rubnog problema, funkcija
takvi da je
U diferencijalnoj
jednadžbi rubnog problema, funkcija
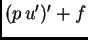 je jednaka
nulfunkciji. To možemo na drugi način iskazati tako da zahtijevamo
da je funkcija
je jednaka
nulfunkciji. To možemo na drugi način iskazati tako da zahtijevamo
da je funkcija
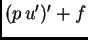 okomita na
okomita na 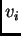 za svaki
za svaki 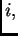 pa
nepoznati koeficijenti
pa
nepoznati koeficijenti 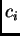 moraju zadovoljavati sljedeće jednadžbe
Problem je u tome što je to beskonačno mnogo
jednadžbi s beskonačno mnogo nepoznanica. Zato uzmemo konačno mnogo
funkcija iz baze
i rješenje pretpostavimo u obliku
Nepoznate koeficijente
moraju zadovoljavati sljedeće jednadžbe
Problem je u tome što je to beskonačno mnogo
jednadžbi s beskonačno mnogo nepoznanica. Zato uzmemo konačno mnogo
funkcija iz baze
i rješenje pretpostavimo u obliku
Nepoznate koeficijente
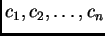 određujemo iz sustava
jednadžbi
Ovaj sustav jednadžbi možemo prepisati u obliku
Stavimo
Tada sustav poprima oblik
odnosno matrično
određujemo iz sustava
jednadžbi
Ovaj sustav jednadžbi možemo prepisati u obliku
Stavimo
Tada sustav poprima oblik
odnosno matrično
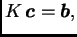 |
(3.33) |
gdje je
![$ K = [K_{ij}],\; \boldsymbol{c}=[c_j],\;
\boldsymbol{b}=[b_i].$](img3344.png)
U ovom slučaju se u formuli za 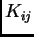 može jednom parcijalno
integrirati pa, uzevši u obzir rubne uvjete, imamo
može jednom parcijalno
integrirati pa, uzevši u obzir rubne uvjete, imamo
Na taj
način sustav jednadžbi (3.34) postaje identičan
onome kod Ritzove metode. To se događa ako rubni problem ispunjava
određene uvjete, o čemu ovdje nećemo detaljnije govoriti.
Istaknimo ovdje bitnu razliku u ideji između Ritzove i Galerkinove
metode. Nužan uvjet za primjenu Ritzove metode je bila egzistencija
varijacijske formulacije rubnog problema u kojoj se pojavljuje
funkcional energije, dok za Galerkinovu metodu to uopće nije važno.
Formalno, Galerkinova metoda se može primijeniti uvijek, pa i u
slučaju nelinearnih rubnih problema. Tada sustav jednadžbi koji
dobijemo nije više linearan.





Next: Parcijalne diferencijalne jednadžbe
Up: Rubni problem
Previous: Metoda konačnih elemenata
Sadržaj
Indeks
2001-10-26
![]() baza
baza
![]() u
u ![]() i skalarni produkt u
i skalarni produkt u ![]() Tada je
Tada je
![]() nulvektor, ako i samo ako je
nulvektor, ako i samo ako je
![]() okomit na
okomit na
![]() za svaki
za svaki ![]() Ta tvrdnja je jasna, ako za
Ta tvrdnja je jasna, ako za ![]() uzmemo vektorski prostor radijvektora u prostoru ili ravnini.
uzmemo vektorski prostor radijvektora u prostoru ili ravnini.
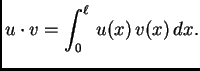
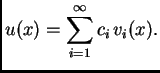
![$\displaystyle \int_0^{\ell}\,\left[\left(p(x)\,\left(\sum_{i=1}^{\infty}
c_i\,v_i(x)\right)'\right)' + f(x)\right]\,v_j(x)\,dx = 0,\qquad
j=1,2,3,\ldots\ .$](img3445.png)
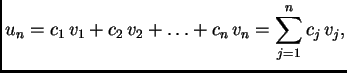
![$\displaystyle \int_0^{\ell}\,\left[\left(p(x)\,\left(\sum_{j=1}^n
c_j\,v_j(x)\right)'\right)' + f(x)\right]\,v_i(x)\,dx = 0,\qquad
i=1,2,3,\ldots,n.$](img3448.png)
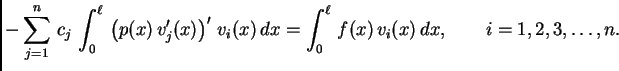
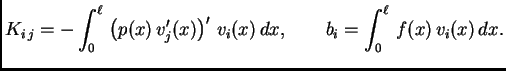
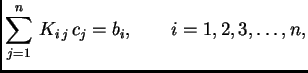
![]() može jednom parcijalno
integrirati pa, uzevši u obzir rubne uvjete, imamo
može jednom parcijalno
integrirati pa, uzevši u obzir rubne uvjete, imamo