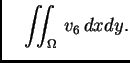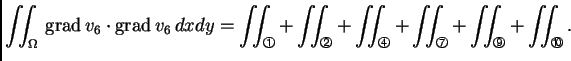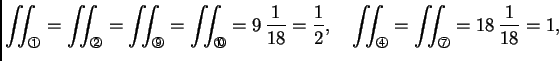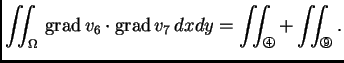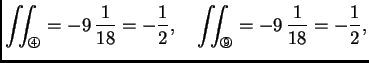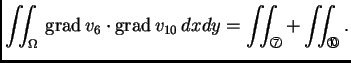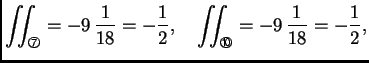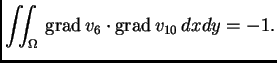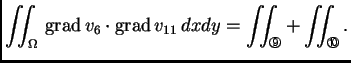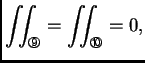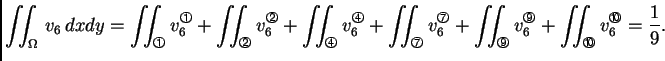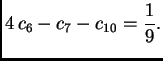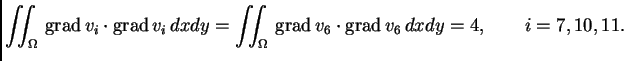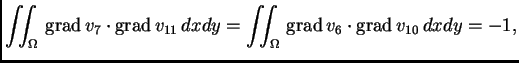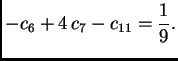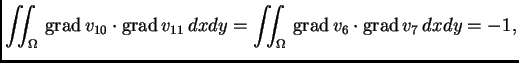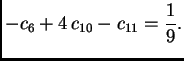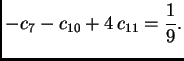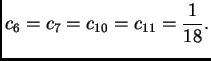Navedene nedostatke donekle ispravlja metoda konačnih elemenata.
Područje  podijelimo jednostavnim likovima (trokutima
četverokutima i sl.) na dijelove, elemente. Vrhove elemenata
zovemo čvorovima. Podjela se vrši tako da niti jedan čvor
ne leži na stranici nekog drugog čvora. Numeriramo elemente i
čvorove. Čvorove treba pažljivo numerirati, da matrica sustava
koji ćemo konačno dobiti bude što uža, tj. da pojas oko glavne
dijagonale izvan kojeg su same nule bude što uži. Zatim odaberemo
koordinatne funkcije
podijelimo jednostavnim likovima (trokutima
četverokutima i sl.) na dijelove, elemente. Vrhove elemenata
zovemo čvorovima. Podjela se vrši tako da niti jedan čvor
ne leži na stranici nekog drugog čvora. Numeriramo elemente i
čvorove. Čvorove treba pažljivo numerirati, da matrica sustava
koji ćemo konačno dobiti bude što uža, tj. da pojas oko glavne
dijagonale izvan kojeg su same nule bude što uži. Zatim odaberemo
koordinatne funkcije
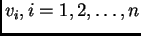 tako da
tako da 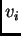 u čvoru
u čvoru 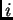 ima vrijednost
ima vrijednost 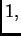 a u ostalim čvorovima vrijednost
a u ostalim čvorovima vrijednost 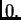 Na
elementima, koji nemaju čvor
Na
elementima, koji nemaju čvor 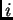 kao vrh,
kao vrh, 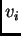 ima vrijednost
ima vrijednost  Na elementima, koji imaju čvor
Na elementima, koji imaju čvor 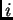 kao svoj vrh, funkciju
kao svoj vrh, funkciju 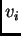 definiramo kao polinom prvog stupnja ili viših stupnjeva ako to
zahtijeva problem koji rješavamo. Objasnimo sada na jednom
jednostavnom primjeru metodu konačnih elemenata za problem ravnoteže
membrane.
definiramo kao polinom prvog stupnja ili viših stupnjeva ako to
zahtijeva problem koji rješavamo. Objasnimo sada na jednom
jednostavnom primjeru metodu konačnih elemenata za problem ravnoteže
membrane.
Primjer 3.22
Neka na napetu kvadratnu membranu
u ravnini
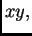
duljine
stranice
učvršćene na rubu, treba riješiti sljedeći
rubni problem ravnoteže membrane
Rješenje. Kvadrat 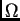 stranice
stranice 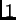 možemo uzeti u ravnini
možemo uzeti u ravnini 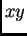 tako
da su mu vrhovi točke
tako
da su mu vrhovi točke
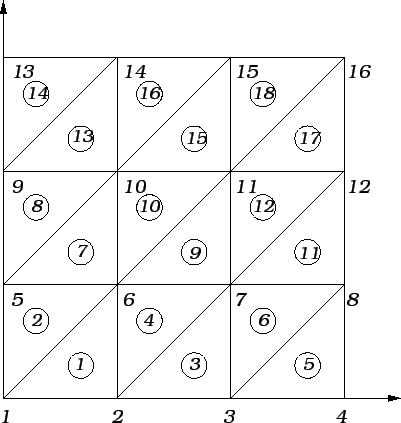
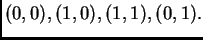 Podijelimo ga na
devet jednakih kvadrata i zatim svaki od tih kvadrata na dva trokuta.
Time je
Podijelimo ga na
devet jednakih kvadrata i zatim svaki od tih kvadrata na dva trokuta.
Time je  podijeljen na 18 elemenata (trokuta). Također
imamo 16 čvorova, od toga 12 na rubu. To su točke
podijeljen na 18 elemenata (trokuta). Također
imamo 16 čvorova, od toga 12 na rubu. To su točke
Na ovoj slici su brojevima označeni čvorovi, a brojevima u
kružnicama konačni elementi (u ovom slučaju trokuti).
Funkcional energije u ovom slučaju je
Prema
varijacijskom principu (
2.59)
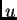
minimizira ovaj
funkcional uz zadovoljavanje Dirichletovog rubnog uvjeta, ako i samo
ako je ispunjen Bernoullijev princip, tj. ako i samo ako vrijedi
(
2.58) za svaku dopustivu funkciju
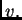
Za svaki čvor definiramo koordinatnu funkciju
tako da stavimo
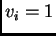
u
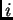
-tom čvoru, a u ostalim čvorovima
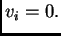
Na elementu
koji ima
-ti čvor kao vrh stavimo
Tako
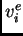
predstavlja restrikciju koordinatne funkcije
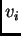
na
konačnom elementu
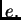
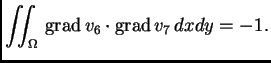
Na primjer za 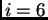 imamo
imamo
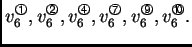 Nađimo
Nađimo
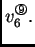 Zbog svojstva koordinatnih
funkcija imamo
Zbog svojstva koordinatnih
funkcija imamo
Rješenje je
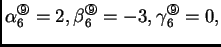
pa je
Na isti način možemo naći da je
a također
i ostale koordinatne funkcije. Primijetimo da je zbog geometrijskih
razloga
Rješenje tražimo
u obliku
U čvoru na rubu, na pr. prvom,
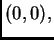
funkcija
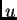
se poništava. Dakle
U prvom čvoru funkcija
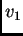
prima vrijednost
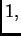
a ostale funkcije
primaju vrijednost
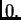
Tako imamo
Za svaki čvor na rubu možemo na taj način dobiti da je, zbog uvjeta
na rubu, pripadni koeficijent jednak
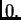
Tako imamo
Preostaje dakle
Dakle zadatak je odrediti koeficijente
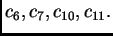
To
ćemo učiniti tako da u Bernoullijev princip (
2.13)
uvrstimo ovaj
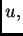
i redom
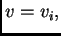
gdje je
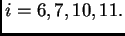
Tako imamo
Da bi se dobila jednadžba za čvor
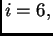
treba izračunati
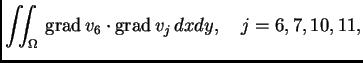
i
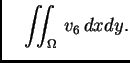
Integral po
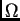
je suma integrala po elementima. Zbog svojstava
koordinatnih funkcija, integral po mnogim elementima iščezava. Na
pr.
Tako je
i prema tome
Zatim
pa je
i prema tome
pa je
i prema tome
pa je
i prema tome
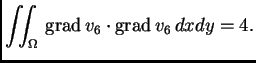
Osim toga je
Isti rezultat dobivamo i ako umjesto
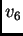
stavimo
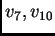
ili
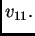
Tako je jednadžba za čvor
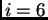
Također je očito
pa jednadžba za čvor
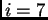
glasi
pa jednadžbe za čvorove
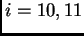
glase
Rješenje sustava je
To su ujedno vrijednosti funkcije
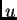
u čvorovima
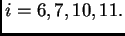
![]() podijelimo jednostavnim likovima (trokutima
četverokutima i sl.) na dijelove, elemente. Vrhove elemenata
zovemo čvorovima. Podjela se vrši tako da niti jedan čvor
ne leži na stranici nekog drugog čvora. Numeriramo elemente i
čvorove. Čvorove treba pažljivo numerirati, da matrica sustava
koji ćemo konačno dobiti bude što uža, tj. da pojas oko glavne
dijagonale izvan kojeg su same nule bude što uži. Zatim odaberemo
koordinatne funkcije
podijelimo jednostavnim likovima (trokutima
četverokutima i sl.) na dijelove, elemente. Vrhove elemenata
zovemo čvorovima. Podjela se vrši tako da niti jedan čvor
ne leži na stranici nekog drugog čvora. Numeriramo elemente i
čvorove. Čvorove treba pažljivo numerirati, da matrica sustava
koji ćemo konačno dobiti bude što uža, tj. da pojas oko glavne
dijagonale izvan kojeg su same nule bude što uži. Zatim odaberemo
koordinatne funkcije
![]() tako da
tako da ![]() u čvoru
u čvoru ![]() ima vrijednost
ima vrijednost ![]() a u ostalim čvorovima vrijednost
a u ostalim čvorovima vrijednost ![]() Na
elementima, koji nemaju čvor
Na
elementima, koji nemaju čvor ![]() kao vrh,
kao vrh, ![]() ima vrijednost
ima vrijednost ![]() Na elementima, koji imaju čvor
Na elementima, koji imaju čvor ![]() kao svoj vrh, funkciju
kao svoj vrh, funkciju ![]() definiramo kao polinom prvog stupnja ili viših stupnjeva ako to
zahtijeva problem koji rješavamo. Objasnimo sada na jednom
jednostavnom primjeru metodu konačnih elemenata za problem ravnoteže
membrane.
definiramo kao polinom prvog stupnja ili viših stupnjeva ako to
zahtijeva problem koji rješavamo. Objasnimo sada na jednom
jednostavnom primjeru metodu konačnih elemenata za problem ravnoteže
membrane.
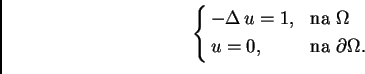
![]() stranice
stranice ![]() možemo uzeti u ravnini
možemo uzeti u ravnini ![]() tako
da su mu vrhovi točke
tako
da su mu vrhovi točke
![]() Podijelimo ga na
devet jednakih kvadrata i zatim svaki od tih kvadrata na dva trokuta.
Time je
Podijelimo ga na
devet jednakih kvadrata i zatim svaki od tih kvadrata na dva trokuta.
Time je ![]() podijeljen na 18 elemenata (trokuta). Također
imamo 16 čvorova, od toga 12 na rubu. To su točke
podijeljen na 18 elemenata (trokuta). Također
imamo 16 čvorova, od toga 12 na rubu. To su točke
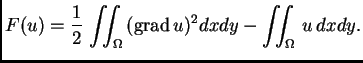
![]() imamo
imamo
![]() Nađimo
Nađimo
![]() Zbog svojstva koordinatnih
funkcija imamo
Zbog svojstva koordinatnih
funkcija imamo
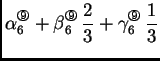
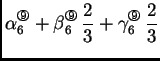
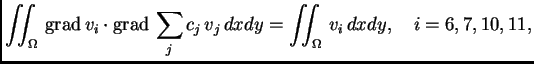
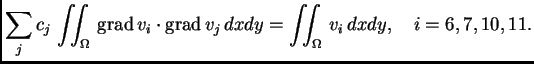
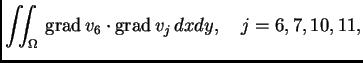 i
i