Next: Numerička matematika
Up: Višedimenzionalni problemi
Previous: Metoda separacije varijabli za
Sadržaj
Indeks
Varijacijski princip
Rješavamo rubni problem
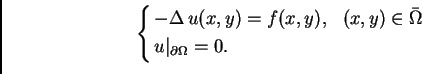 |
(2.55) |
Svaku funkciju 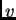 klase
klase
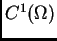 takvu da je
takvu da je
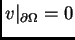 zovemo dopustivom
funkcijom.
zovemo dopustivom
funkcijom.
Pretpostavimo da je 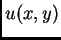 ravnotežni položaj membrane, tj.
rješenje gornjeg problema. Da bi se membrana pomakla iz tog
položaja, potrebno je izvršiti neki rad. Taj rad ovisi o veličini
perturbacije
ravnotežni položaj membrane, tj.
rješenje gornjeg problema. Da bi se membrana pomakla iz tog
položaja, potrebno je izvršiti neki rad. Taj rad ovisi o veličini
perturbacije 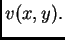 Budući da je u novom položaju membrana i
dalje učvršćena na rubu, mora i
Budući da je u novom položaju membrana i
dalje učvršćena na rubu, mora i 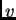 biti dopustiva funkcija. Rad,
koji izvrši vanjska sila uslijed pomaka
biti dopustiva funkcija. Rad,
koji izvrši vanjska sila uslijed pomaka 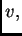 je
je
dok je unutrašnji rad membrane
Ako jednadžbu u (2.57) pomnožimo s 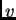 i integriramo po
i integriramo po
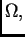 dobivamo
Ova jednakost
izražava Bernoullijev princip sačuvanja rada (energije). Iz prve
Greenove formule
slijedi
jer je
dobivamo
Ova jednakost
izražava Bernoullijev princip sačuvanja rada (energije). Iz prve
Greenove formule
slijedi
jer je 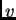 dopustiva funkcija, pa iščezava na rubu od
dopustiva funkcija, pa iščezava na rubu od 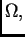 a
s njom i krivuljni integral. Kad to uvrstimo u gornju jednakost,
dobivamo
a
s njom i krivuljni integral. Kad to uvrstimo u gornju jednakost,
dobivamo
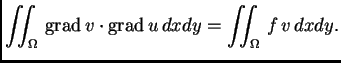 |
(2.56) |
Možemo zaključiti sljedeće. Ako funkcija 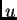 rješava rubni problem
(2.57), onda za svaku dopustivu funkciju
rješava rubni problem
(2.57), onda za svaku dopustivu funkciju 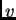 vrijedi
(2.58). Također vrijedi i obrat. Ako
vrijedi
(2.58). Također vrijedi i obrat. Ako 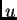 sa svojstvom
sa svojstvom
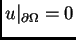 zadovoljava (2.58) za svaku
dopustivu funkciju
zadovoljava (2.58) za svaku
dopustivu funkciju 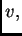 onda
onda 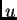 rješava rubni problem (2.57).
rješava rubni problem (2.57).
Prvi dio smo dokazali. Treba dokazati obrat.
Neka vrijedi (2.58) za svaku dopustivu funkciju 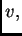 i neka
je
i neka
je
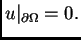 Tada je prema prvoj Greenovoj formuli
Tada je prema prvoj Greenovoj formuli
Krivuljni integral iščezava, jer je 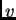 dopustiva funkcija. Tako je
Uvrstimo u (2.58), dobivamo
za svaku dopustivu funkciju
dopustiva funkcija. Tako je
Uvrstimo u (2.58), dobivamo
za svaku dopustivu funkciju 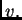 Po osnovnoj lemi slijedi
Po osnovnoj lemi slijedi
Kao i u jednodimenzionalnom slučaju sada dokazujemo da je
Bernoullijev princip ekvivalentan problemu minimizacije
funkcionala
energije.
Neka je dan funkcional
Pogledajmo čime se odlikuje 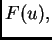 ako
ako 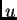 zadovoljava Bernoullijev
princip, tj. zadovoljava (2.58). U tu svrhu stavimo
zadovoljava Bernoullijev
princip, tj. zadovoljava (2.58). U tu svrhu stavimo
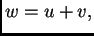 gdje je
gdje je 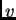 perturbacija
ravnotežnog položaja (dopustiva funkcija). Kako je
perturbacija
ravnotežnog položaja (dopustiva funkcija). Kako je 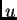 ravnotežni
položaj,
ravnotežni
položaj, 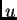 je dopustiva funkcija, pa je i
je dopustiva funkcija, pa je i 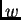 dopustiva. Imamo
Dakle
dopustiva. Imamo
Dakle
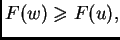 i pri tom je
i pri tom je 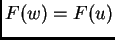 samo ako je
samo ako je
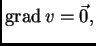 a to znači
a to znači
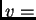 konst.
konst.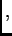 a kako je na rubu
a kako je na rubu
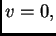 slijedi da je
slijedi da je 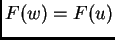 samo ako je
samo ako je 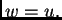 Dakle
Dakle 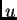 je
jedinstvena funkcija sa svojstvom
je
jedinstvena funkcija sa svojstvom
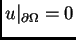 koja
minimizira funkcional
koja
minimizira funkcional 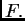
Dokažimo sada obrat, tj. da funkcija 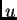 koja minimizira funkcional
koja minimizira funkcional
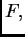 i zadovoljava rubni uvjet
i zadovoljava rubni uvjet
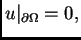 mora
zadovoljavati Bernoullijev princip, tj.
(2.58). Pretpostavimo da
mora
zadovoljavati Bernoullijev princip, tj.
(2.58). Pretpostavimo da 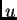 ima tražena svojstva, i
stavimo
ima tražena svojstva, i
stavimo
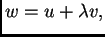 gdje je
gdje je 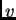 perturbacija (funkcija iz klase
dopustivih). Funkcional
perturbacija (funkcija iz klase
dopustivih). Funkcional 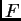 poprima minimum na funkciji
poprima minimum na funkciji 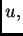 pa prema
tome funkcija
pa prema
tome funkcija
poprima minimum za
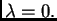 Imamo
Imamo
Ovo je polinom drugog stupnja u
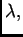 koeficijent uz
koeficijent uz
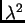 je pozitivan, pa funkcija doista ima minimum u
tjemenu. Apscisa tjemena parabole, koja je graf funkcije
je
pa ako se minimum dostiže u
je pozitivan, pa funkcija doista ima minimum u
tjemenu. Apscisa tjemena parabole, koja je graf funkcije
je
pa ako se minimum dostiže u
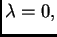 tj. u točki s apscisom
tj. u točki s apscisom
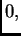 onda mora biti
onda mora biti 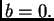 U našem slučaju slijedi
za svaku
dopustivu funkciju
U našem slučaju slijedi
za svaku
dopustivu funkciju 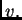 Tako smo dokazali da
Tako smo dokazali da 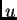 zadovoljava
(2.58). Iz svega rečenog možemo zaključiti da vrijedi
sljedeće.
zadovoljava
(2.58). Iz svega rečenog možemo zaključiti da vrijedi
sljedeće.
Teorem 21 (
Varijacijski
princip)
Da
bi funkcija
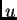
bila rješenje rubnog problema
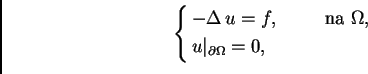 |
(2.57) |
nužno je i dovoljno da funkcija 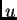 zadovoljava taj rubni uvjet i da
minimizira funkcional
zadovoljava taj rubni uvjet i da
minimizira funkcional





Next: Numerička matematika
Up: Višedimenzionalni problemi
Previous: Metoda separacije varijabli za
Sadržaj
Indeks
2001-10-26
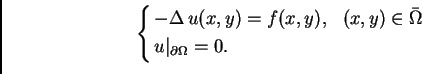
![]() ravnotežni položaj membrane, tj.
rješenje gornjeg problema. Da bi se membrana pomakla iz tog
položaja, potrebno je izvršiti neki rad. Taj rad ovisi o veličini
perturbacije
ravnotežni položaj membrane, tj.
rješenje gornjeg problema. Da bi se membrana pomakla iz tog
položaja, potrebno je izvršiti neki rad. Taj rad ovisi o veličini
perturbacije ![]() Budući da je u novom položaju membrana i
dalje učvršćena na rubu, mora i
Budući da je u novom položaju membrana i
dalje učvršćena na rubu, mora i ![]() biti dopustiva funkcija. Rad,
koji izvrši vanjska sila uslijed pomaka
biti dopustiva funkcija. Rad,
koji izvrši vanjska sila uslijed pomaka ![]() je
je
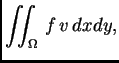
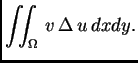
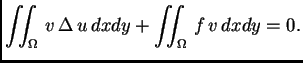
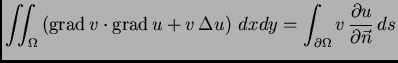
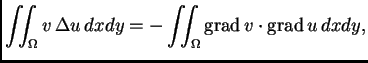
![]() rješava rubni problem
(2.57), onda za svaku dopustivu funkciju
rješava rubni problem
(2.57), onda za svaku dopustivu funkciju ![]() vrijedi
(2.58). Također vrijedi i obrat. Ako
vrijedi
(2.58). Također vrijedi i obrat. Ako ![]() sa svojstvom
sa svojstvom
![]() zadovoljava (2.58) za svaku
dopustivu funkciju
zadovoljava (2.58) za svaku
dopustivu funkciju ![]() onda
onda ![]() rješava rubni problem (2.57).
rješava rubni problem (2.57).
![]() i neka
je
i neka
je
![]() Tada je prema prvoj Greenovoj formuli
Tada je prema prvoj Greenovoj formuli
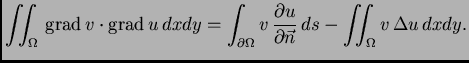
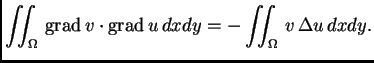
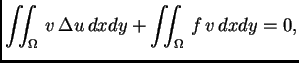
![$\displaystyle \iint_{\Omega}\,\left[\Delta u + f\right]\,v\,dxdy = 0,$](img2290.png)
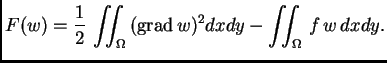
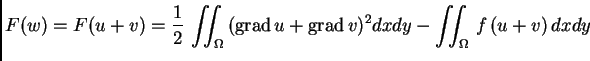
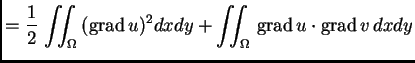
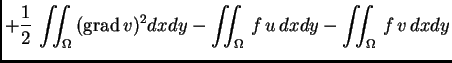

![]() koja minimizira funkcional
koja minimizira funkcional
![]() i zadovoljava rubni uvjet
i zadovoljava rubni uvjet
![]() mora
zadovoljavati Bernoullijev princip, tj.
(2.58). Pretpostavimo da
mora
zadovoljavati Bernoullijev princip, tj.
(2.58). Pretpostavimo da ![]() ima tražena svojstva, i
stavimo
ima tražena svojstva, i
stavimo
![]() gdje je
gdje je ![]() perturbacija (funkcija iz klase
dopustivih). Funkcional
perturbacija (funkcija iz klase
dopustivih). Funkcional ![]() poprima minimum na funkciji
poprima minimum na funkciji ![]() pa prema
tome funkcija
pa prema
tome funkcija
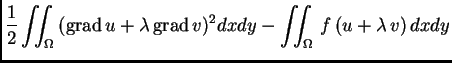
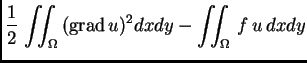
![% latex2html id marker 37249
$\displaystyle + \lambda{}\left[\iint_{\Omega}\,{\rm grad\,}u\cdot{\rm grad\,}v\,dxdy - \iint_{\Omega}\,
f\,v\,dxdy\right]$](img2310.png)
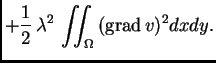
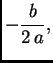

![]() zadovoljava taj rubni uvjet i da
minimizira funkcional
zadovoljava taj rubni uvjet i da
minimizira funkcional