




Next: Koncentrirano djelovanje
Up: Jedinstvenost rješenja
Previous: III. Oba uvjeta dinamička.
Sadržaj
Indeks
Uvjet 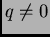 znači ustvari da je
znači ustvari da je 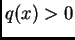 za barem jedan
za barem jedan 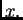 U
ovom slučaju sva tri rubna problema imaju jedinstveno rješenje. To
ćemo dokazati pomoću energetske
jednadžbe.
U
ovom slučaju sva tri rubna problema imaju jedinstveno rješenje. To
ćemo dokazati pomoću energetske
jednadžbe.
Jednom parcijalno integriramo prvi integral
i rezultat uvrstimo. Dobivamo
Ova jednadžba se zove energetska jednadžba. Naziv ima opravdanje u
sljedećem razmatranju.
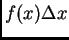 predstavlja približno vanjsku
silu koja djeluje na komadić žice
predstavlja približno vanjsku
silu koja djeluje na komadić žice 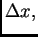 a
a
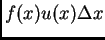 je rad te sile na putu progiba
je rad te sile na putu progiba 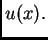 Prema tome zadnji integral na
lijevoj strani jednadžbe (2.13) je rad vanjske sile koji
djeluje na cijelu žicu na putu progiba. Sila otpora je
Prema tome zadnji integral na
lijevoj strani jednadžbe (2.13) je rad vanjske sile koji
djeluje na cijelu žicu na putu progiba. Sila otpora je
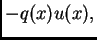 pa je srednji integral ukupni rad sile otpora duž cijele žice na
putu progiba. Prvi integral predstavlja energiju deformacije,
pa je srednji integral ukupni rad sile otpora duž cijele žice na
putu progiba. Prvi integral predstavlja energiju deformacije,
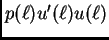 je rad kontaktne sile na desnom rubu na
putu
je rad kontaktne sile na desnom rubu na
putu
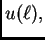 a
a
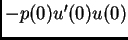 je rad kontaktne sile na lijevom
rubu na putu
je rad kontaktne sile na lijevom
rubu na putu 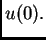
Neka su 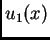 i
i 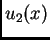 dva rješenja bilo kojeg od tri rubna
problema koja promatramo. Funkcija
dva rješenja bilo kojeg od tri rubna
problema koja promatramo. Funkcija
rješava
homogenu jednadžbu
i
pri tom zadovoljava homogene rubne uvjete. Energetska jednadžba
(2.13) sada glasi
Budući da je 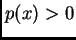 i
i
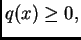 slijedi
Kako je podintegralna funkcija neprekidna,
nenegativna, i njezin je integral duž žice jednak
slijedi
Kako je podintegralna funkcija neprekidna,
nenegativna, i njezin je integral duž žice jednak 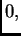 slijedi da je
sama podintegralna funkcija jednaka nuli
Zbroj dvije
nenegativne funkcije može biti jednak nuli samo tako da je svaka od
njih jednaka nuli. Tako je
pa je
slijedi da je
sama podintegralna funkcija jednaka nuli
Zbroj dvije
nenegativne funkcije može biti jednak nuli samo tako da je svaka od
njih jednaka nuli. Tako je
pa je 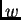 konstanta, tj.
konstanta, tj. 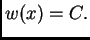 S druge strane je
Kako je
S druge strane je
Kako je 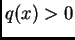 za barem jedan
za barem jedan 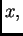 slijedi da je
slijedi da je 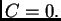 Prema tome
tj.
Dakle rješenje je doista jedinstveno.
Prema tome
tj.
Dakle rješenje je doista jedinstveno.





Next: Koncentrirano djelovanje
Up: Jedinstvenost rješenja
Previous: III. Oba uvjeta dinamička.
Sadržaj
Indeks
2001-10-26
![]() znači ustvari da je
znači ustvari da je ![]() za barem jedan
za barem jedan ![]() U
ovom slučaju sva tri rubna problema imaju jedinstveno rješenje. To
ćemo dokazati pomoću energetske
jednadžbe.
U
ovom slučaju sva tri rubna problema imaju jedinstveno rješenje. To
ćemo dokazati pomoću energetske
jednadžbe.
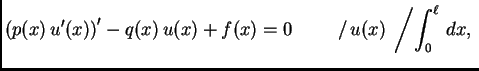
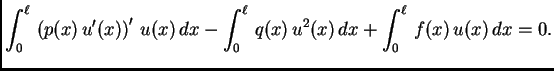
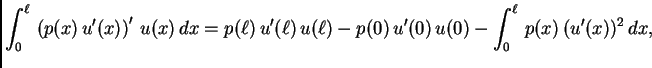
![]() i
i ![]() dva rješenja bilo kojeg od tri rubna
problema koja promatramo. Funkcija
dva rješenja bilo kojeg od tri rubna
problema koja promatramo. Funkcija
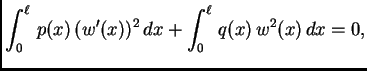
![$\displaystyle \int_0^{\ell}\,\left[p(x)\,(w'(x))^2 +
q(x)\,w^2(x)\right]\, dx = 0.$](img1354.png)