U dosadašnjim razmatranjima vanjska sila je bila zadana po jedinici
duljine, što znači da je ![]() gustoća sile (linearna kad se
radi o jednodimenzionalnom objektu kao što je žica). Ako je u točki
gustoća sile (linearna kad se
radi o jednodimenzionalnom objektu kao što je žica). Ako je u točki
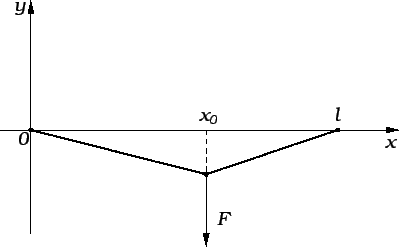
![]() napete žice obješen uteg mase
napete žice obješen uteg mase ![]() onda kažemo da se radi o
koncentriranom djelovanju. U
tom slučaju ne vrijedi izvod
zakona o sačuvanju količine gibanja u 2.1.1.
onda kažemo da se radi o
koncentriranom djelovanju. U
tom slučaju ne vrijedi izvod
zakona o sačuvanju količine gibanja u 2.1.1.
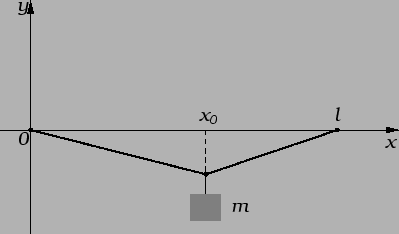
Pretpostavimo da masa utega nije prevelika, tako da se ne događa
kidanje žice niti plastična deformacija. To znači da je progib
![]() kao funkcija od
kao funkcija od ![]() neprekidna
funkcija, tj.
neprekidna
funkcija, tj.
Promatrajmo mali komad žice
![]() oko
točke
oko
točke ![]() Promjena količine gibanja tog komada žice u jedinici
vremena jednaka je sili koja djeluje na taj komad
Promjena količine gibanja tog komada žice u jedinici
vremena jednaka je sili koja djeluje na taj komad
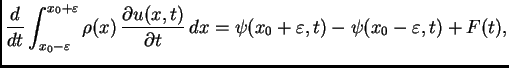
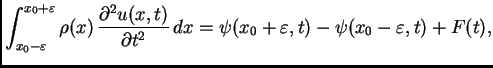
Promjena količine
gibanja u jedinici vremena je veličina koja se neprekidno mijenja u
vremenu, pa je
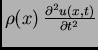 neprekidna funkcija. Odatle, po teoremu srednje
vrijednosti za integrale
neprekidna funkcija. Odatle, po teoremu srednje
vrijednosti za integrale
![$\displaystyle \lim_{\varepsilon\rightarrow 0+}
\int_{x_0-\varepsilon}^{x_0+\va...
...\,\varepsilon\,\rho(\xi)\,\frac{\partial^2 u(\xi,t)}{\partial
t^2}\right] = 0.$](img1377.png)
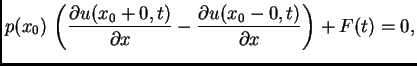
Za funkciju, koja u točki ![]() ima konačan limes slijeve strane i
konačan limes s desne strane,ali se ti limesi razlikuju, kažemo da
ima u točki
ima konačan limes slijeve strane i
konačan limes s desne strane,ali se ti limesi razlikuju, kažemo da
ima u točki ![]() prekid prve vrste.
prekid prve vrste.
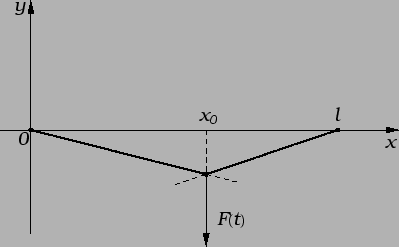
Rješenje. Na intervalima
![]()
![]() i
i
![]() nemamo koncentriranih niti drugih
vanjskih sila, pa je na njima jednadžba
nemamo koncentriranih niti drugih
vanjskih sila, pa je na njima jednadžba
na 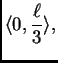 |
||
na 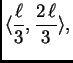 |
||
na 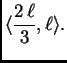 |
| 0 | |||
| 0 | |||
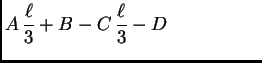 |
0 | ||
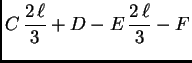 |
0 | ||
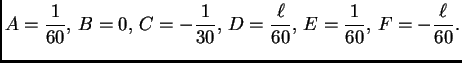
![% latex2html id marker 34553
$\displaystyle u(x) = \begin{cases}
\frac{1}{60}\,x...
...rac{\ell}{60},& \quad \mbox{za $ x \in
[\frac{2\,\ell}{3},\ell].$}
\end{cases}$](img1407.png)