




Next: Dijagonalizacija simetrične matrice
Up: Problem vlastitih ...
Previous: Problem vlastitih ...
Sadržaj
Indeks
Vlastite vrijednosti i vlastiti vektori
Definicija 13
Neka je
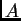
kvadratna matrica reda
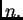
Za broj
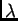
kažemo da
je
vlastita (svojstvena) vrijednost
matrice
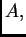
a za vektor
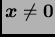
kažemo da je
vlastiti (svojstveni)
vektor matrice
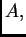
ako vrijedi
Skup svih vlastitih vrijednosti matrice 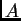 se zove spektar matrice
se zove spektar matrice
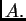
Na slici 1.15 je prikazano nekoliko vektora i njihovih slika
dobivenih djelovanjem matrice
![\begin{displaymath}
% latex2html id marker 31951
\left[
\begin{array}{cc}
2 & -1 \\ -1 & 2
\end{array}\right].\end{displaymath}](img590.png) Uočite razliku između djelovanja na vektore
Uočite razliku između djelovanja na vektore
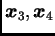 i na ostale vektore. Slike vektora
i na ostale vektore. Slike vektora
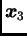 i
i
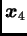 su ostale na pravcima
određenim s tim vektorima (original i slika su kolinearni), dok druge
vektore matrica zakreće.
su ostale na pravcima
određenim s tim vektorima (original i slika su kolinearni), dok druge
vektore matrica zakreće.
Slika 1.15:
Djelovanje matrice drugog reda na vektore u ravnini.
|
|
Neka je
Tada je
također
Dakle, ako je
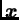 vlastiti vektor za vlastitu vrijednost
vlastiti vektor za vlastitu vrijednost
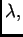 onda je i svaki s njim kolinearan vektor također vlastiti
vektor koji pripada istoj vlastitoj vrijednosti. (Na slici
1.15 su crticama označeni pravci čija svaka točka
predstavlja vrh nekog vlastitog vektora. Na jednom pravcu leže
vlastiti vektori koji pripadaju vlastitoj vrijednosti
onda je i svaki s njim kolinearan vektor također vlastiti
vektor koji pripada istoj vlastitoj vrijednosti. (Na slici
1.15 su crticama označeni pravci čija svaka točka
predstavlja vrh nekog vlastitog vektora. Na jednom pravcu leže
vlastiti vektori koji pripadaju vlastitoj vrijednosti 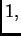 a na drugom
oni koji pripadaju vlastitoj vrijednosti
a na drugom
oni koji pripadaju vlastitoj vrijednosti  )
)
Jednadžba
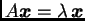 se može
drukčije napisati kao
se može
drukčije napisati kao
Da se nađe
vlastiti vektor, potrebno je riješiti ovu matričnu jednadžbu. Ako
je
![$ A=[a_{ij}],$](img599.png) i
i
![$ \boldsymbol{x}=[x_i],$](img600.png) ta jednadžba se može
napisati kao sustav linearnih algebarskih jednadžbi
ta jednadžba se može
napisati kao sustav linearnih algebarskih jednadžbi
Ovo je homogen sustav i on ima netrivijalno
rješenje, ako i samo ako je determinanta sustava jednaka nuli. Dakle,
Ako raspišemo ovu determinantu i jednadžbu pomnožimo s 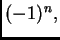 dobivamo algebarsku jednadžbu
dobivamo algebarsku jednadžbu 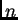 -tog reda
Ova jednadžba se zove karakteristična jednadžba matrice
-tog reda
Ova jednadžba se zove karakteristična jednadžba matrice 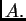 Polinom na
lijevoj strani se zove karakteristični polinom
matrice
Polinom na
lijevoj strani se zove karakteristični polinom
matrice 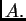 Pri tom je
Pri tom je
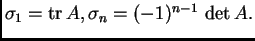
Poznato je da algebarska jednadžba  -tog reda ima
-tog reda ima  općenito
kompleksnih rješenja, računajući njihovu kratnost. Ta rješenja su
vlastite vrijednosti.
općenito
kompleksnih rješenja, računajući njihovu kratnost. Ta rješenja su
vlastite vrijednosti.
Uvrštavanjem pojedinog rješenja u gornji homogeni sustav,
dobivamo sustav jednadžbi koji, zbog toga što je homogen i što je
determinanta jednaka nuli, ima beskonačno mnogo rješenja. To je u
skladu s činjenicom da je svaki vektor, kolinearan s vlastitim
vektorom, također vlastiti. Budući da vlastite vrijednosti mogu biti
kompleksni brojevi, kao rješenja tog sustava možemo dobiti
vektore čije su komponente kompleksni brojevi. Nas će prvenstveno
interesirati slučaj kada su vlastite vrijednosti i vlastiti vektori
realni.
Primjer 1.24
Nađimo vlastite vrijednosti i vlastite vektore matrice
Rješenje. Karakteristična jednadžba je
Vlastite vrijednosti su dakle
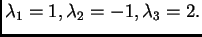
Za
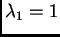 pripadni vlastiti vektor dobivamo (iz
(1.5)) kao rješenje sustava
pripadni vlastiti vektor dobivamo (iz
(1.5)) kao rješenje sustava
Iz druge jednadžbe imamo
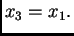
Uvrstimo u treću i dobivamo
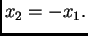
Tako je vlastiti vektor
Za
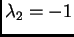
imamo sustav
Rješenja su
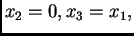
pa je vlastiti vektor
Za
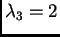
imamo sustav
Rješenja su
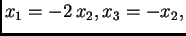
pa je vlastiti vektor
Na slici
1.16 se vide vlastiti vektori i njihove slike.
Slika 1.16:
Vlastiti vektori i njihove slike (različite vlastite vrijednosti).
|
|
Prvi vektor je preslikan u samog sebe. Isto se događa sa svakim
drugim radijvektorom, kolinearnim s prvim
vektorom. Drugi se preslika u sebi suprotan, što se događa i sa
svakim s njim kolinearnim radijvektorom. Treći se preslika u
dvostruko dulji (rastegne se), što se događa i sa svakim s njim
kolinearnim radijvektorom. Vektor koji ne leži niti na jednom od
pravaca određenih ovim vektorima, biva preslikan u vektor koji
nije kolinearan sa svojim originalom.
Teorem 8
(Hamilton-Cayley)
Ako je polinom
karakteristični polinom matrice
onda je
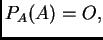
tj.
Dokaz.
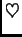





Next: Dijagonalizacija simetrične matrice
Up: Problem vlastitih ...
Previous: Problem vlastitih ...
Sadržaj
Indeks
2001-10-26
![]() se zove spektar matrice
se zove spektar matrice
![]()
![]() se zove spektar matrice
se zove spektar matrice
![]()
![\begin{displaymath}
% latex2html id marker 31951
\left[
\begin{array}{cc}
2 & -1 \\ -1 & 2
\end{array}\right].\end{displaymath}](img590.png) Uočite razliku između djelovanja na vektore
Uočite razliku između djelovanja na vektore
![]() i na ostale vektore. Slike vektora
i na ostale vektore. Slike vektora
![]() i
i
![]() su ostale na pravcima
određenim s tim vektorima (original i slika su kolinearni), dok druge
vektore matrica zakreće.
su ostale na pravcima
određenim s tim vektorima (original i slika su kolinearni), dok druge
vektore matrica zakreće.
![]() se može
drukčije napisati kao
se može
drukčije napisati kao
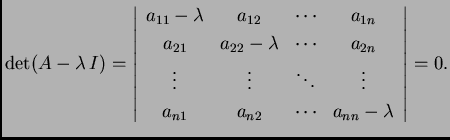
![]() -tog reda ima
-tog reda ima ![]() općenito
kompleksnih rješenja, računajući njihovu kratnost. Ta rješenja su
vlastite vrijednosti.
općenito
kompleksnih rješenja, računajući njihovu kratnost. Ta rješenja su
vlastite vrijednosti.
![% latex2html id marker 32021
$\displaystyle A=\left[ \begin{array}{ccc}
3 & -2 & -4 \\
-1 & 1 & 1 \\
1 & -2 & -2
\end{array} \right].$](img608.png)
![]() pripadni vlastiti vektor dobivamo (iz
(1.5)) kao rješenje sustava
pripadni vlastiti vektor dobivamo (iz
(1.5)) kao rješenje sustava
![% latex2html id marker 32049
$\displaystyle \left[\begin{array}{c}
x_1 \\ -x_1...
...nd{array}\right]=x_1\left[\begin{array}{c}
1 \\ -1 \\ 1
\end{array}\right].$](img617.png)
![% latex2html id marker 32071
$\displaystyle \left[\begin{array}{c}
x_1 \\ 0 \\...
...end{array}\right]=x_1\left[\begin{array}{c}
1 \\ 0 \\ 1
\end{array}\right].$](img623.png)
![% latex2html id marker 32093
$\displaystyle \left[\begin{array}{c}
-2\,x_2 \\ ...
...d{array}\right]=x_2\left[\begin{array}{c}
-2 \\ 1 \\ -1
\end{array}\right].$](img628.png)