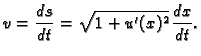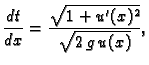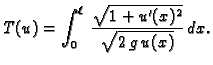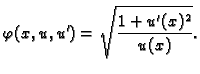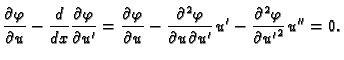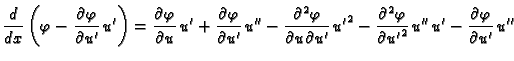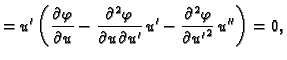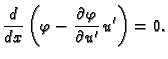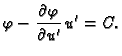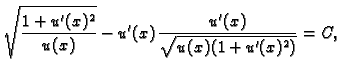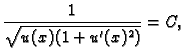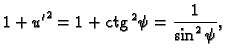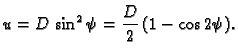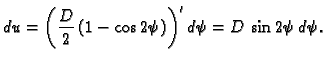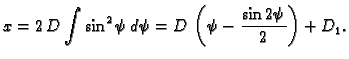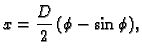



Next: Višedimenzionalni problemi
Up: Rubni problemi
Previous: Fourierova metoda
Contents
Index
Subsections
Varijacijske metode
Varijacijski princip
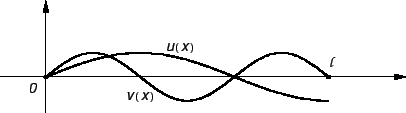
Neka je zadan rubni problem ravnoteže žice
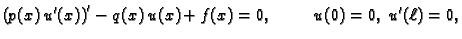 |
(2.30) |
i pretpostavimo da je  ravnotežni položaj. Pretpostavljamo da je
proizvoljni pomak iz položaja ravnoteže žice određen neprekidnom
funkcijom
ravnotežni položaj. Pretpostavljamo da je
proizvoljni pomak iz položaja ravnoteže žice određen neprekidnom
funkcijom  klase
klase
![$ C^1[0,\ell],$](img1777.gif) takvom da je
takvom da je 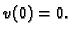 Nazovimo sve takve funkcije dopustivima. Funkciju
Nazovimo sve takve funkcije dopustivima. Funkciju
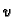 ćemo zvati perturbacijom ravnotežnog stanja
(položaja). Naglasimo da je
ćemo zvati perturbacijom ravnotežnog stanja
(položaja). Naglasimo da je 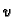 pomak od ravnotežnog stanja a ne od osi
pomak od ravnotežnog stanja a ne od osi
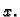 Ako jednadžbu iz (2.30) pomnožimo s
Ako jednadžbu iz (2.30) pomnožimo s 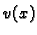 i integriramo
duž žice, dobit ćemo
Parcijalno integrirajmo prvi integral
Zbog
i integriramo
duž žice, dobit ćemo
Parcijalno integrirajmo prvi integral
Zbog
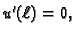 i
i 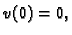 slijedi
slijedi
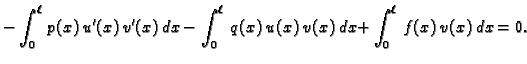 |
(2.31) |
Jednakost (2.31) predstavlja Bernoullijev princip
sačuvanja rada. Prvi član je rad kontaktne sile
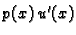 koja se opire deformaciji
koja se opire deformaciji 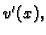 iz ravnotežnog stanja. Drugi član
je rad sile otpora, a treći rad vanjske sile čija je gustoća
iz ravnotežnog stanja. Drugi član
je rad sile otpora, a treći rad vanjske sile čija je gustoća 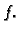 Bernoullijev princip tvrdi da je ukupni rad vanjskih i unutarnjih sila
na perturbaciji ravnotežnog položaja jednak
Bernoullijev princip tvrdi da je ukupni rad vanjskih i unutarnjih sila
na perturbaciji ravnotežnog položaja jednak 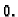 Drugim riječima,
ako žicu perturbiramo, svaki komadić žice prijeđe neki put iz
ravnotežnog stanja. Vanjske sile na tom putu izvrše neki rad. Rad
uslijed sile napetosti žice, koja nastoji vratiti žicu u ravnotežni
položaj jednak je po apsolutnom iznosu radu vanjskih sila, ali
suprotnog predznaka. Tako je suma svih radova jednaka nuli.
Možemo zaključiti sljedeće. Ako
Drugim riječima,
ako žicu perturbiramo, svaki komadić žice prijeđe neki put iz
ravnotežnog stanja. Vanjske sile na tom putu izvrše neki rad. Rad
uslijed sile napetosti žice, koja nastoji vratiti žicu u ravnotežni
položaj jednak je po apsolutnom iznosu radu vanjskih sila, ali
suprotnog predznaka. Tako je suma svih radova jednaka nuli.
Možemo zaključiti sljedeće. Ako  rješava zadani rubni
problem, onda vrijedi jednakost (2.31) za svaku
dopustivu funkciju (perturbaciju)
rješava zadani rubni
problem, onda vrijedi jednakost (2.31) za svaku
dopustivu funkciju (perturbaciju) 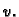
Pretpostavimo da je funkcija  takva da je
takva da je 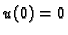 i da zadovoljava
uvjet (Bernoullijev princip)
i da zadovoljava
uvjet (Bernoullijev princip)
za svaku dopustivu funkciju 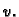 Integrirajmo parcijalno prvi član
na lijevoj strani. Dobivamo
Za dopustivu funkciju
Integrirajmo parcijalno prvi član
na lijevoj strani. Dobivamo
Za dopustivu funkciju 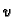 to je, zbog
to je, zbog 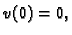
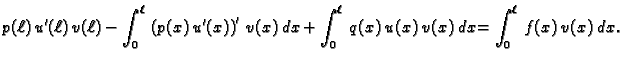 |
(2.32) |
Ovo vrijedi za svaku dopustivu funkciju, pa i takvu za koju
je
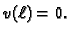 Za takvu
Za takvu  ova jednakost postaje
odnosno
ova jednakost postaje
odnosno
Na temelju ove leme zaključujemo da je nužno
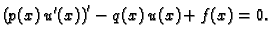 |
(2.33) |
Dakle  zadovoljava diferencijalnu jednadžbu. Po pretpostavci
zadovoljava homogeni kinematički uvjet
zadovoljava diferencijalnu jednadžbu. Po pretpostavci
zadovoljava homogeni kinematički uvjet 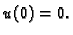 Dokažimo na kraju
da
Dokažimo na kraju
da  zadovoljava i dinamički uvjet
zadovoljava i dinamički uvjet
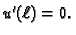 Zbog
(2.33), jednadžba (2.32) se sada svodi na
Kako ona vrijedi za svaku dopustivu funkciju, vrijedi i za
takvu za koju je
Zbog
(2.33), jednadžba (2.32) se sada svodi na
Kako ona vrijedi za svaku dopustivu funkciju, vrijedi i za
takvu za koju je
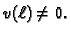 Osim toga je
Osim toga je
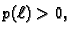 pa
prema tome mora biti
pa
prema tome mora biti
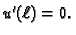
Možemo zaključiti sljedeće. Ako  zadovoljava
Bernoullijev princip, i
zadovoljava
Bernoullijev princip, i 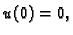 onda
onda  rješava rubni problem
(2.30).
rješava rubni problem
(2.30).
Tako smo dokazali sljedeći teorem.
Primijetimo da se u drugoj tvrdnji zahtijeva od funkcije  samo
zadovoljavanje kinematičkog rubnog uvjeta, dok dinamički rubni
uvjet,
samo
zadovoljavanje kinematičkog rubnog uvjeta, dok dinamički rubni
uvjet,
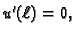 nužno slijedi iz činjenice da
nužno slijedi iz činjenice da  zadovoljava
Bernoullijev princip.
zadovoljava
Bernoullijev princip.
Promatrajmo i dalje rubni problem (2.34). Stavimo
gdje je  ravnotežni položaj,
ravnotežni položaj, 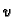 perturbacija, a
perturbacija, a 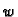 rezultanta. Svakom takvom rezultantnom položaju
rezultanta. Svakom takvom rezultantnom položaju 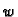 možemo
pridružiti broj
možemo
pridružiti broj
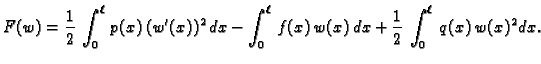 |
(2.36) |
Prema tome tu se radi o funkciji koja funkcijama 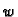 pridružuje
brojeve (kao na pr. kod Riemannovog integrala). Takva funkcija se zove
funkcional. Prvi integral je unutrašnja potencijalna
energija uslijed deformacije žice, drugi integral je potencijalna
energija vanjske sile, dok je treći integral potencijalna energija
elastične sile otpora. Zato se ovaj funkcional zove
funkcional energije.
pridružuje
brojeve (kao na pr. kod Riemannovog integrala). Takva funkcija se zove
funkcional. Prvi integral je unutrašnja potencijalna
energija uslijed deformacije žice, drugi integral je potencijalna
energija vanjske sile, dok je treći integral potencijalna energija
elastične sile otpora. Zato se ovaj funkcional zove
funkcional energije.
Interesira nas čime se odlikuje ravnotežno stanje  , među svim
mogućim funkcijama
, među svim
mogućim funkcijama 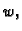 u odnosu na ponašanje funkcionala
u odnosu na ponašanje funkcionala 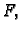 zadanog
formulom (2.36). Neka je
zadanog
formulom (2.36). Neka je
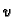 dopustiva funkcija. Podsjetimo da to znači da je
dopustiva funkcija. Podsjetimo da to znači da je 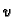 klase
klase
![$ C^1[0,\ell],$](img1777.gif) i da je
i da je 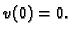 Neka je
Neka je 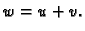 U formulama, koje
slijede, nećemo pisati varijablu
U formulama, koje
slijede, nećemo pisati varijablu 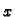 radi kratkoće.
radi kratkoće.
Drugi član je nenegativan zato jer je takva podintegralna funkcija, a
treći je nula zbog Bernoullijevog principa. Tako imamo
Dakle možemo zaključiti sljedeće. Od svih rezultanti 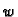 ona
rezultanta, koja predstavlja ravnotežni položaj, pridaje
funkcionalu
ona
rezultanta, koja predstavlja ravnotežni položaj, pridaje
funkcionalu 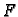 najmanju vrijednost. Za funkciju na kojoj funkcional
najmanju vrijednost. Za funkciju na kojoj funkcional
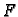 poprima najmanju vrijednost kažemo da minimizira
funkcional
poprima najmanju vrijednost kažemo da minimizira
funkcional 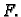 Tako smo dokazali prvu tvrdnju sljedećeg teorema.
Tako smo dokazali prvu tvrdnju sljedećeg teorema.
Teorem 18
(Varijacijski princip, Dirichletov princip)
- 1.
- Neka je funkcija
![$ u\in C^2[0,\ell]$](img1821.gif) rješenje rubnog problema
(2.34). Tada
rješenje rubnog problema
(2.34). Tada  minimizira funkcional
minimizira funkcional 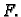
- 2.
- Neka je funkcija
![$ u\in C^2[0,\ell],$](img1823.gif) neka je
neka je 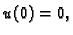 i
neka
i
neka  minimizira funkcional
minimizira funkcional 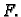 Tada je
Tada je  rješenje rubnog
problema (2.34).
rješenje rubnog
problema (2.34).
Dokažimo drugu tvrdnju (obrat prve). Pretpostavimo da  minimizira
funkcional
minimizira
funkcional 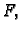 tj. da je
tj. da je
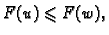 za proizvoljnu
dopustivu funkciju
za proizvoljnu
dopustivu funkciju 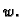 Ako je
Ako je 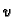 dopustiva funkcija, onda je i
dopustiva funkcija, onda je i
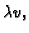 za
neki
za
neki
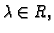 dopustiva. Stavimo
dopustiva. Stavimo
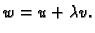
Tako vidimo da je
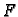 polinom drugog stupnja u
varijabli
polinom drugog stupnja u
varijabli 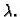 Graf polinoma drugog stupnja je parabola. Kako je
koeficijent uz
Graf polinoma drugog stupnja je parabola. Kako je
koeficijent uz 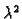 pozitivan parabola ima u svom tjemenu
minimum. Apscisa tjemena je
pozitivan parabola ima u svom tjemenu
minimum. Apscisa tjemena je
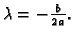 Da bi se minimum
dogodio za
Da bi se minimum
dogodio za
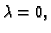 što se mora desiti jer smo pretpostavili da
je
što se mora desiti jer smo pretpostavili da
je
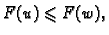 mora nužno biti
mora nužno biti 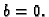 To znači da mora biti
Dopustiva funkcija
To znači da mora biti
Dopustiva funkcija 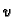 je bila proizvoljna, pa prema tome ova jednakost vrijedi za svaku
dopustivu funkciju
je bila proizvoljna, pa prema tome ova jednakost vrijedi za svaku
dopustivu funkciju 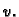 Osim toga pretpostavka je da je
Osim toga pretpostavka je da je 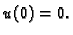 Odatle, po Bernoullijevom principu slijedi da
Odatle, po Bernoullijevom principu slijedi da  rješava rubni
problem (2.34).
rješava rubni
problem (2.34).
Primijetimo na kraju da teorem 18 izražava poznati
mehanički princip da je ravnotežno stanje fizikalnog sustava ono
stanje u kojem je njegova potencijalna energija minimalna.
Rješenje rubnog problema treba biti funkcija iz
![$ C^2[0,\ell].$](img1850.gif) S druge
strane za funkciju koja minimizira funkcional energije dovoljno je da
bude iz
S druge
strane za funkciju koja minimizira funkcional energije dovoljno je da
bude iz
![$ C^1[0,\ell].$](img1851.gif)
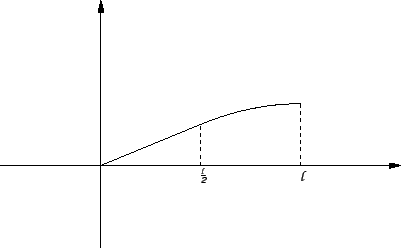
Sljedeći primjer pokazuje da rubni problem ne mora imati
rješenja, dok za pripadni funkcional energije postoji funkcija koja ga
minimizira. Radi jednostavnosti promatrat ćemo rubni problem u kojem
je 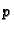 konstanta, i
konstanta, i 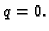
Primjer 2.19
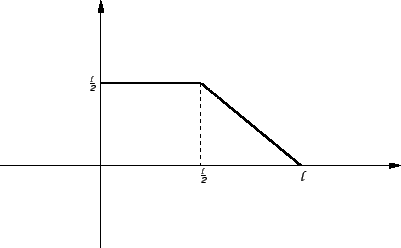
Neka je gustoća vanjske sile dana formulom
Rubni problem
 |
(2.37) |
nema rješenja.
Problem minimizacije pripadnog funkcionala
uz rubne uvjete
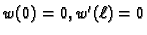
ima rješenje, tj. postoji
funkcija

takva da je
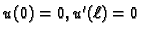
i da je
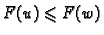
za svaku isto takvu funkciju
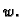
Rješenje. Rubni problem ne može imati rješenje, jer ako funkcija
![$ u\in C^2[0,\ell]$](img1821.gif) rješava rubni problem, onda je
rješava rubni problem, onda je
neprekidna funkcija na
![$ [0,\ell],$](img1798.gif)
što nije istina.
Da bismo našli funkciju koja minimizira funkcional, integrirajmo
jednadžbu u (2.37) po području od 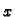 do
do 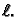
Zbog uvjeta
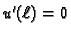
na rubu, prvi član iščezava, pa je
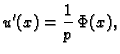 |
(2.38) |
gdje je
Nakon što integriramo (
2.38) od 0 do
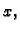
i uzmemo u obzir
uvjet
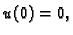
dobivamo
Funkcija
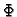
je neprekidna, pa je tako
![$ u\in C^1[0,\ell].$](img1869.gif)
Pokažimo sada da ova funkcija minimizira pripadni funkcional energije.
Stavimo
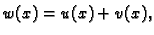 gdje je
gdje je 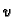 proizvoljna dopustiva funkcija.
proizvoljna dopustiva funkcija.
Jedino drugi član ovisi o
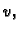
i on je nenegativan. Najmanju
vrijednost poprima onda kada je
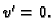
No tada je
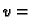
const.
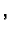
pa zbog
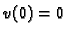
je
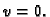
Pri tom minimum iznosi
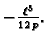
Prema tome funkcija

doista minimizira funkcional
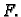
S druge
strane
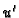
nema tangentu u
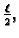
pa ne postoji
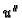
na
![$ [0,\ell].$](img1625.gif)
Tako

ne može biti rješenje rubnog problema
(
2.37).
Primjer 2.20
Naći skalarnu funkciju
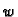
na segmentu
![$ [0,T],$](img1886.gif)
koja minimizira funkcional
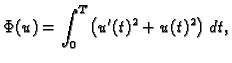 |
(2.39) |
uz početni uvjet
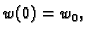
i izračunati minimum funkcionala
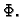
Rješenje. Stavimo
gdje je
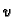
proizvoljna dopustiva funkcija (neprekidno derivabilna i
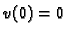
), a
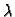
proizvoljan broj.
Da bi
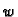
minimizirala dani funkcional, mora
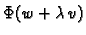
imati minimalnu vrijednost za
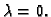
No,
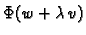
je polinom drugog stupnja u
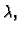
njegov graf je parabola, pa se
minimalna vrijednost dostiže u tjemenu. Apscisa tjemena je
Kako se minimum ostvaruje za
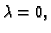
nužno mora biti
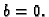
U ovom slučaju je
Slijedi
Drugi integral parcijalno integriramo
pa imamo, zbog
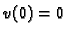
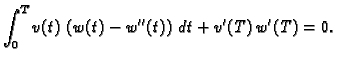 |
(2.40) |
Ova jednakost vrijedi za svaku dopustivu funkciju, pa i za svaku takvu
za koju je
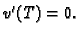
Zaključujemo da je
za svaku takvu funkciju
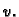
Odatle slijedi
Prema tome integral u (
2.40) iščezava, pa je
za svaku dopustivu funkciju, pa i za takve za koje je
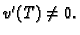
Slijedi
Dakle, problem minimizacije funkcionala (2.39) vodi na
rješavanje rubnog problema
Rješenje je
Minimalna vrijednost funkcionala, uz zadani poz1etni uvjet
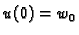
je
Varijacijski račun
U 2.4.1 smo razmatrali problem minimizacije funkcionala
energije određenog rubnog problema. Ovdje ćemo razmatrati problem
minimizacije općenitijeg funkcionala.
Neka je dana neprekidno derivabilna funkcija od tri varijable
Neka je 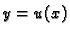 i
i 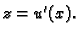 Tada imamo kompoziciju
funkcija (složenu funkciju) od jedne varijable
U vezi s tom funkcijom možemo promatrati sljedeći funkcional
Ovo je općenitiji funkcional od onih koje smo promatrali. Na pr. ako
stavimo
onda kompozicija kao gore daje funkcional energije (2.36).
Tada imamo kompoziciju
funkcija (složenu funkciju) od jedne varijable
U vezi s tom funkcijom možemo promatrati sljedeći funkcional
Ovo je općenitiji funkcional od onih koje smo promatrali. Na pr. ako
stavimo
onda kompozicija kao gore daje funkcional energije (2.36).
Osim same formule, važno je odrediti domenu funkcionala. Kao što se
iz formule vidi, funkcional 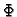 pridružuje funkciji
pridružuje funkciji  broj. Važno je definirati kojem skupu funkcija pripada
broj. Važno je definirati kojem skupu funkcija pripada 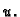 To naravno
ovisi o problemu o kojem se radi. Pretpostavimo da je funkcional
To naravno
ovisi o problemu o kojem se radi. Pretpostavimo da je funkcional
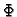 definiran na skupu
definiran na skupu
Skup 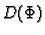 je vektorski prostor, jer je bilo koja linearna
kombinacija elemenata iz
je vektorski prostor, jer je bilo koja linearna
kombinacija elemenata iz 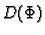 opet element iz
opet element iz 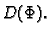 Elemente
iz
Elemente
iz 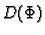 ćemo zvati dopustivim funkcijama.
ćemo zvati dopustivim funkcijama.
Posebno nas interesiraju funkcije na kojima funkcional poprima
minimalnu ili maksimalnu vrijednost. Svaka takva funkcija se zove
ekstremala. Nađimo sada uvjet koji treba ispunjavati
funkcija 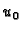 da bude ekstremala funkcionala
da bude ekstremala funkcionala 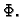 U tu svrhu
stavimo
U tu svrhu
stavimo
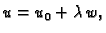 gdje je
gdje je 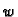 dopustiva funkcija.
dopustiva funkcija.
je funkcija od 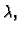 i za
i za 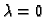 ona ima ekstrem. Budući da je
funkcija
neprekidno derivabilna, to znači da mora biti
ona ima ekstrem. Budući da je
funkcija
neprekidno derivabilna, to znači da mora biti
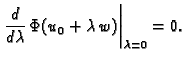 |
(2.41) |
Kako je 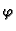 neprekidno derivabilna, imamo
Preciznije
Zbog (2.41) imamo
neprekidno derivabilna, imamo
Preciznije
Zbog (2.41) imamo
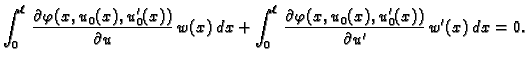 |
(2.42) |
Jednom parcijalno integrirajmo drugi
integral
Funkcija 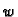 je dopustiva, pa je
je dopustiva, pa je 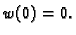 Tako imamo
Kad to uvrstimo u (2.42), dobivamo
Tako imamo
Kad to uvrstimo u (2.42), dobivamo
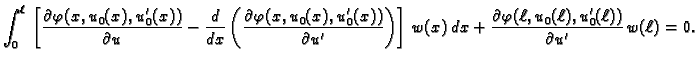 |
(2.43) |
Ova jednakost vrijedi za svaku dopustivu funkciju, pa i za takve za
koje je
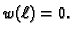 Za takve dopustive funkcije imamo
Na osnovu leme 2 slijedi
ili kraće
Za takve dopustive funkcije imamo
Na osnovu leme 2 slijedi
ili kraće
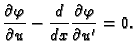 |
(2.44) |
Ako se s time vratimo u jednadžbu (2.43), te zbog
proizvoljnosti dopustive funkcije 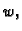 uzmemo
uzmemo 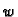 takvu da je
takvu da je
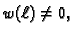 slijedi da mora vrijediti također
Ova jednakost se zove prirodni uvjet na rubu
slijedi da mora vrijediti također
Ova jednakost se zove prirodni uvjet na rubu 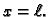
Jednadžba (2.44) se zove Eulerova diferencijalna
jednadžba za dani funkcional. Dakle, da bi funkcija  bila
ekstremala funkcionala
bila
ekstremala funkcionala 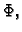 nužno mora zadovoljavati pripadnu
Eulerovu diferencijalnu jednadžbu. To je nužan uvjet, ali ne i
dovoljan. Dovoljne uvjete ovdje nećemo razmatrati. Napomenimo da se
iz prirode problema često može zaključiti da li ekstremala postoji
ili ne. Ako postoji, i ima neprekidne derivacije dovoljno visokog
reda, onda je dovoljno naći rješenje Eulerove jednadžbe, koje
zadovoljava rubne uvjete.
nužno mora zadovoljavati pripadnu
Eulerovu diferencijalnu jednadžbu. To je nužan uvjet, ali ne i
dovoljan. Dovoljne uvjete ovdje nećemo razmatrati. Napomenimo da se
iz prirode problema često može zaključiti da li ekstremala postoji
ili ne. Ako postoji, i ima neprekidne derivacije dovoljno visokog
reda, onda je dovoljno naći rješenje Eulerove jednadžbe, koje
zadovoljava rubne uvjete.
Primjer 2.21
Problem brahistohrone. Interesira nas koji oblik putanje
treba izabrati tako da se za najkraće vrijeme, u polju sile teže,
stigne iz točke
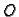
u točku
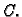
Krivulja s tim svojstvom se zove
brahistohrona.
2.1
Rješenje. Zakon o sačuvanju energije glasi
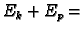
konst.
Nadalje
Predznak
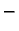
dolazi stoga što smo pozitivni dio osi
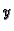
okrenuli
prema dolje. Tako je
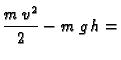
konst.
U točki
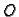
je
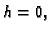
i
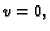
pa slijedi da je konstanta jednaka
nuli. Odatle
jer ćemo u daljnjem visinu označavati s
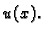
Zadatak je naći
funkciju
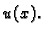
S druge strane brzina je
Odatle je
pa je vrijeme gibanja po krivulji
Od svih puteva
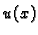
treba izabrati onaj uz koji ovaj funkcional
poprima najmanju vrijednost uz uvjete
Budući da konstanta
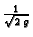
ne utječe na to da li je

ekstremala ili ne, možemo uzeti
Budući da u
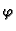
ne dolazi eksplicitno
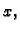
Eulerova jednadžba
glasi
S druge strane
jer je izraz u zagradi upravo lijeva strana Eulerove jednadžbe. Dakle
Odatle
U našem slučaju
tj.
Stavimo
gdje je
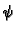
parametar.
pa je
Sada treba
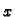
izraziti kao funkciju od
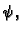
pa ćemo tako dobiti
parametarski određenu traženu krivulju.
Isto tako
Tako je
Odatle
Mora biti
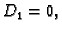
da bi istovremeno
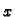
i
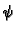
težili k
nuli. Stavimo
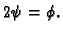
Tada je
dok je
Konstanta
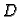
se određuje iz preostalog rubnog uvjeta
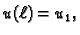
ili preciznije
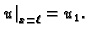
Ove parametarske
jednadžbe predstavljaju cikloidu.




Next: Višedimenzionalni problemi
Up: Rubni problemi
Previous: Fourierova metoda
Contents
Index
Salih Suljagic
1999-12-17

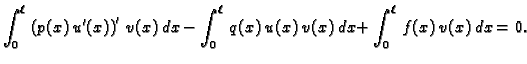
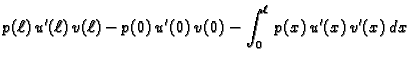
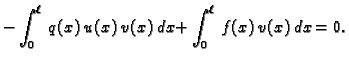
![]() takva da je
takva da je ![]() i da zadovoljava
uvjet (Bernoullijev princip)
i da zadovoljava
uvjet (Bernoullijev princip)
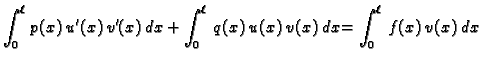
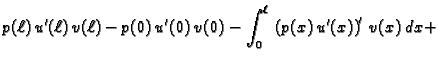
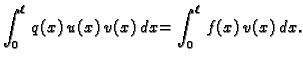
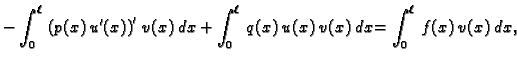
![$\displaystyle \int_0^{\ell}\,\left[\left(p(x)\,u'(x)\right)' - q(x)\,u(x)
+ f(x)\right]v(x)\,dx = 0.$](img1797.gif)
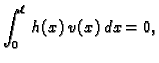
![]() onda zbog
neprekidnosti funkcije
onda zbog
neprekidnosti funkcije ![]() postoji točka
postoji točka
![]() blizu točke
blizu točke ![]() takva da je
takva da je ![]() Isto
možemo zaključiti i za desni rub
Isto
možemo zaključiti i za desni rub ![]() Odatle slijedi da je
dovoljno dokazati tvrdnju leme za
Odatle slijedi da je
dovoljno dokazati tvrdnju leme za
![]()
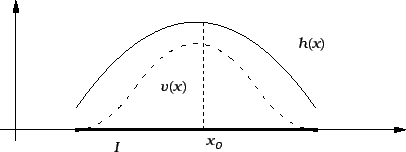
![]() takav da je
takav da je ![]() Tada, zbog neprekidnosti
funkcije
Tada, zbog neprekidnosti
funkcije ![]() postoji interval
postoji interval ![]() oko točke
oko točke ![]() takav da je
takav da je
![]() za svaki
za svaki ![]() Izaberimo neprekidnu funkciju
Izaberimo neprekidnu funkciju ![]() tako da
je
tako da
je ![]() za svaki
za svaki
![]() i da je
i da je ![]() za
svaki
za
svaki ![]()
![]() zadovoljava
Bernoullijev princip, i
zadovoljava
Bernoullijev princip, i ![]() onda
onda ![]() rješava rubni problem
(2.30).
rješava rubni problem
(2.30).
![]() samo
zadovoljavanje kinematičkog rubnog uvjeta, dok dinamički rubni
uvjet,
samo
zadovoljavanje kinematičkog rubnog uvjeta, dok dinamički rubni
uvjet,
![]() nužno slijedi iz činjenice da
nužno slijedi iz činjenice da ![]() zadovoljava
Bernoullijev princip.
zadovoljava
Bernoullijev princip.
![]() , među svim
mogućim funkcijama
, među svim
mogućim funkcijama ![]() u odnosu na ponašanje funkcionala
u odnosu na ponašanje funkcionala ![]() zadanog
formulom (2.36). Neka je
zadanog
formulom (2.36). Neka je
![]() dopustiva funkcija. Podsjetimo da to znači da je
dopustiva funkcija. Podsjetimo da to znači da je ![]() klase
klase
![]() i da je
i da je ![]() Neka je
Neka je ![]() U formulama, koje
slijede, nećemo pisati varijablu
U formulama, koje
slijede, nećemo pisati varijablu ![]() radi kratkoće.
radi kratkoće.
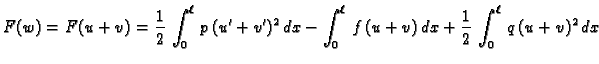
![$\displaystyle =\frac{1}{2}\,\int_0^{\ell}\,p\,\left[u'\,^2+ 2\,u'\,v' + v'\,^2\...
...right]\,dx + \frac{1}{2}\,\int_0^{\ell}\,q\,\left[u^2+
2\,u\,v + v^2\right]\,dx$](img1830.gif)
![$\displaystyle =\underbrace{\frac{1}{2}\,\int_0^{\ell}\,p\,u'\,^2\,dx - \int_0^{...
... \underbrace{\int_0^{\ell}\,
\left[p\,u'\,v' + q\,u\,v - f\,v\right]\,dx}_{=0}.$](img1831.gif)
![]() ona
rezultanta, koja predstavlja ravnotežni položaj, pridaje
funkcionalu
ona
rezultanta, koja predstavlja ravnotežni položaj, pridaje
funkcionalu ![]() najmanju vrijednost. Za funkciju na kojoj funkcional
najmanju vrijednost. Za funkciju na kojoj funkcional
![]() poprima najmanju vrijednost kažemo da minimizira
funkcional
poprima najmanju vrijednost kažemo da minimizira
funkcional ![]() Tako smo dokazali prvu tvrdnju sljedećeg teorema.
Tako smo dokazali prvu tvrdnju sljedećeg teorema.
![]() minimizira
funkcional
minimizira
funkcional ![]() tj. da je
tj. da je
![]() za proizvoljnu
dopustivu funkciju
za proizvoljnu
dopustivu funkciju ![]() Ako je
Ako je ![]() dopustiva funkcija, onda je i
dopustiva funkcija, onda je i
![]() za
neki
za
neki
![]() dopustiva. Stavimo
dopustiva. Stavimo
![]()
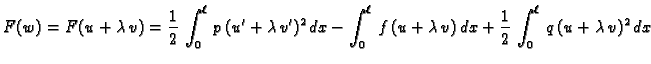
![$\displaystyle = \frac{1}{2}\,\int_0^{\ell}\,p\,\left[u'\,^2+
2\,u'\,\lambda\,v'...
...{2}\,\int_0^{\ell}\,q\,\left[u^2+
2\,u\,\lambda\,v + \lambda^2\,v^2\right]\,dx $](img1841.gif)
![$\displaystyle = \lambda^2\,\underbrace{\frac{1}{2}\,\int_0^{\ell}\,\left[p\,v'\...
...t_0^{\ell}\,
\left[p\,u'\,^2 + q\,u^2\right]\,dx - \int_0^{\ell}\,f\,u\,dx}_{c}$](img1842.gif)
![$\displaystyle \int_0^{\ell}\,\left[p\,u'\,v' + q\,u\,v - f\,v\right]\,dx = 0.$](img1849.gif)
![]() S druge
strane za funkciju koja minimizira funkcional energije dovoljno je da
bude iz
S druge
strane za funkciju koja minimizira funkcional energije dovoljno je da
bude iz
![]()
![]() konstanta, i
konstanta, i ![]()
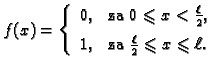
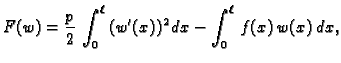
![]() rješava rubni problem, onda je
rješava rubni problem, onda je
![]() do
do ![]()
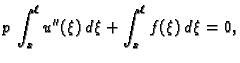
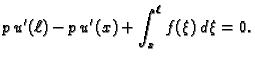
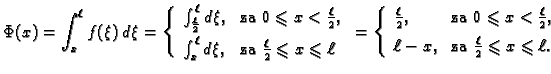
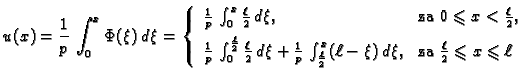

![]() gdje je
gdje je ![]() proizvoljna dopustiva funkcija.
proizvoljna dopustiva funkcija.
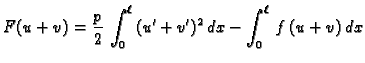
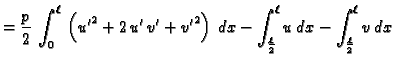
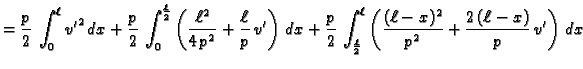
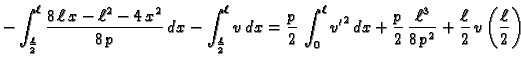
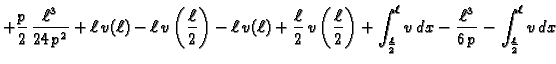
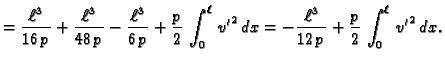
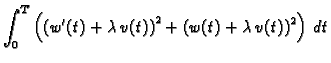
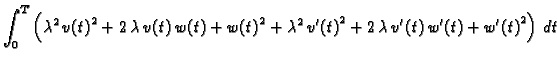
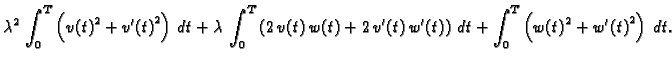
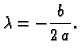
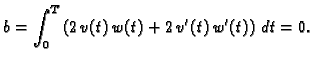
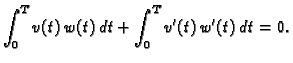
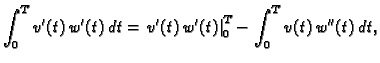
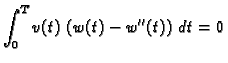
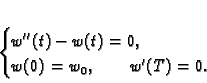
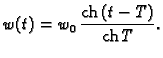
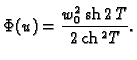
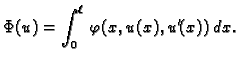
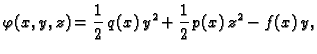
![]() pridružuje funkciji
pridružuje funkciji ![]() broj. Važno je definirati kojem skupu funkcija pripada
broj. Važno je definirati kojem skupu funkcija pripada ![]() To naravno
ovisi o problemu o kojem se radi. Pretpostavimo da je funkcional
To naravno
ovisi o problemu o kojem se radi. Pretpostavimo da je funkcional
![]() definiran na skupu
definiran na skupu
![]() da bude ekstremala funkcionala
da bude ekstremala funkcionala ![]() U tu svrhu
stavimo
U tu svrhu
stavimo
![]() gdje je
gdje je ![]() dopustiva funkcija.
dopustiva funkcija.
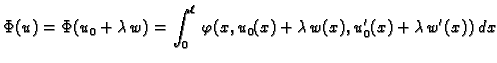
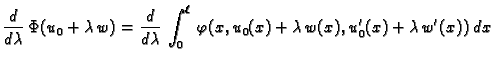
![$\displaystyle = \int_0^{\ell}\,
\frac{d}{d\lambda}\,
\varphi(x,u_0(x)+\lambda\,...
...hi}{\partial u}\,w(x) + \frac{\partial
\varphi}{\partial u'}\,w'(x)\right]\,dx.$](img1929.gif)
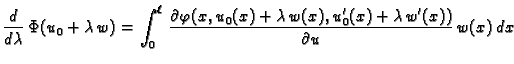
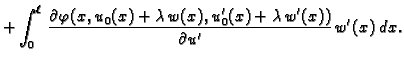
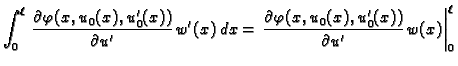
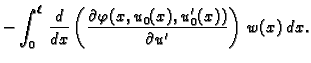
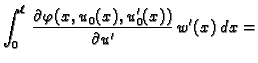
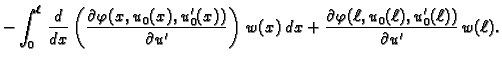
![$\displaystyle \int_0^{\ell}\,\left[\frac{\partial
\varphi(x,u_0(x),u'_0(x))}{\p...
...c{\partial \varphi(x,u_0(x),u'_0(x))}{\partial
u'}\right)\right]\,w(x)\,dx = 0.$](img1940.gif)
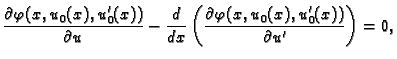
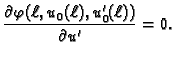
![]() bila
ekstremala funkcionala
bila
ekstremala funkcionala ![]() nužno mora zadovoljavati pripadnu
Eulerovu diferencijalnu jednadžbu. To je nužan uvjet, ali ne i
dovoljan. Dovoljne uvjete ovdje nećemo razmatrati. Napomenimo da se
iz prirode problema često može zaključiti da li ekstremala postoji
ili ne. Ako postoji, i ima neprekidne derivacije dovoljno visokog
reda, onda je dovoljno naći rješenje Eulerove jednadžbe, koje
zadovoljava rubne uvjete.
nužno mora zadovoljavati pripadnu
Eulerovu diferencijalnu jednadžbu. To je nužan uvjet, ali ne i
dovoljan. Dovoljne uvjete ovdje nećemo razmatrati. Napomenimo da se
iz prirode problema često može zaključiti da li ekstremala postoji
ili ne. Ako postoji, i ima neprekidne derivacije dovoljno visokog
reda, onda je dovoljno naći rješenje Eulerove jednadžbe, koje
zadovoljava rubne uvjete.

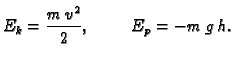
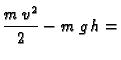 konst.
konst.