



Next: Aproksimacija funkcije i numerička
Up: Numerička matematika
Previous: Rješavanje jednadžbi
Contents
Index
Subsections
Rješavanje sustava jednadžbi
Iterativne metode
Želimo riješiti sustav linearnih algebarskih jednadžbi
koji matrično zapisan glasi
gdje je
To je matrična jednadžba, i mi ćemo često o sustavu jednadžbi
govoriti kao o jednadžbi, misleći na ovu matričnu
jednadžbu. Pretpostavimo da je 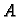 regularna matrica. Tada jednadžba ima
rješenje, i označimo to rješenje sa
regularna matrica. Tada jednadžba ima
rješenje, i označimo to rješenje sa
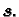
Osnovna ideja iterativnih metoda se sastoji u sljedećem. Stavimo
gdje su 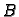 i
i 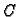 također kvadratne matrice
također kvadratne matrice 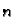 -tog reda. Jednadžbu
tada možemo prepisati kao
Ako s
-tog reda. Jednadžbu
tada možemo prepisati kao
Ako s
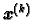 označimo
označimo 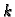 -tu aproksimaciju rješenja,
onda pomoću formule
možemo naći
-tu aproksimaciju rješenja,
onda pomoću formule
možemo naći 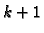 -vu aproksimaciju rješenja.
-vu aproksimaciju rješenja.
Naravno, da bi postupak uopće krenuo, treba biti zadana početna
aproksimacija
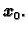 Nadalje, matrica
Nadalje, matrica 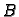 mora biti
regularna i relativno jednostavna, da bismo imali rješenje i da bismo
ga mogli relativno jednostavno izračunati. Također postupak nas mora
približavati k rješenju, tj. postupak mora biti takav da
mora biti
regularna i relativno jednostavna, da bismo imali rješenje i da bismo
ga mogli relativno jednostavno izračunati. Također postupak nas mora
približavati k rješenju, tj. postupak mora biti takav da
Opišimo sada neke od iterativnih metoda.
Jacobijeva metoda
Pretpostavimo da su elementi na glavnoj dijagonali matrice 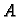 različiti od nule (ako je potrebno, premještanjem redaka u
regularnoj matrici se to uvijek može postići).
Rastavimo
različiti od nule (ako je potrebno, premještanjem redaka u
regularnoj matrici se to uvijek može postići).
Rastavimo 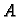 kako slijedi
kako slijedi
gdje je
Tako je 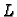 donja,
donja, 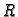 gornja trokutasta, a
gornja trokutasta, a 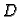 je dijagonalna
matrica. Ako stavimo
imamo iterativni postupak oblika
Budući da su elementi na glavnoj dijagonali matrice
je dijagonalna
matrica. Ako stavimo
imamo iterativni postupak oblika
Budući da su elementi na glavnoj dijagonali matrice 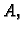 a prema tome
i matrice
a prema tome
i matrice 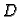 različiti od nule, postoji
različiti od nule, postoji 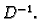 Inverz od
dijagonalne matrice se vrlo lako računa. Iz
Inverz od
dijagonalne matrice se vrlo lako računa. Iz
![$ D=[\delta_{ij}\,a_{ii}]$](img2734.gif) slijedi
slijedi
![$ D^{-1}=[\frac{\delta_{ij}}{a_{ii}}].$](img2735.gif) Tako gornju
jednadžbu možemo pomnožiti s lijeva s
Tako gornju
jednadžbu možemo pomnožiti s lijeva s 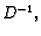 pa imamo sljedeći
algoritam.
pa imamo sljedeći
algoritam.
Algoritam 7
(Jacobijeva metoda)
Proizvoljno izaberemo početnu aproksimaciju
i zatim računamo sljedeće aproksimacije
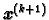
po
formuli
odnosno
gdje je
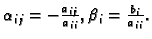
Budući da dijelimo s
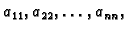 poželjno je, ako je to moguće, poredati retke u matrici
poželjno je, ako je to moguće, poredati retke u matrici 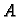 (jednadžbe
u sustavu) tako da svaki element na glavnoj dijagonali bude po apsolutnoj
vrijednosti veći od sume apsolutnih vrijednosti ostalih elemenata u
retku u kojem se nalazi.
(jednadžbe
u sustavu) tako da svaki element na glavnoj dijagonali bude po apsolutnoj
vrijednosti veći od sume apsolutnih vrijednosti ostalih elemenata u
retku u kojem se nalazi.
Gauss-Seidelova metoda
Gauss-Seidelova metoda je poboljšanje Jacobijeve metode u sljedećem
smislu.
Pod pretpostavkom da je
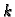 -ta aproksimacija rješenja,
-ta aproksimacija rješenja, 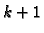 -vu nalazimo iz sustava
-vu nalazimo iz sustava
Dakle
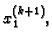 koji smo izračunali iz prve jednadžbe pomoću
komponenti
koji smo izračunali iz prve jednadžbe pomoću
komponenti 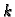 -te aproksimacije rješenja, koristimo odmah u drugoj,
trećoj, ...,
-te aproksimacije rješenja, koristimo odmah u drugoj,
trećoj, ..., 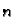 -toj jednadžbi;
-toj jednadžbi;
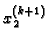 koristimo u
trećoj, četvrtoj, ...,
koristimo u
trećoj, četvrtoj, ..., 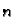 -toj jednadžbi; itd.
Taj sustav možemo zapisati u matričnom obliku
odnosno
Tako imamo formulu iterativnog postupka
Nedostatak ove formule je u tome što treba naći inverz matrice
-toj jednadžbi; itd.
Taj sustav možemo zapisati u matričnom obliku
odnosno
Tako imamo formulu iterativnog postupka
Nedostatak ove formule je u tome što treba naći inverz matrice
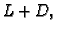 što je teže nego naći inverz od
što je teže nego naći inverz od 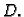 Zato
radimo malo drukčije. Pomnožimo ovu jednadžbu s
Zato
radimo malo drukčije. Pomnožimo ovu jednadžbu s 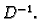 Odatle
Tako dolazimo do sljedećeg algoritma.
Odatle
Tako dolazimo do sljedećeg algoritma.
Algoritam 8
(Gauss-Seidelova metoda)
Izaberemo proizvoljnu početnu aproksimaciju
i zatim računamo sljedeće aproksimacije
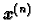
po
formuli
odnosno
gdje je
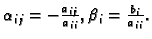
Primjer 3.10
Riješiti sljedeći sustav jednadžbi
Rješenje. Radi jednostavnosti ćemo radije vektorstupac rješenja pisati u
obliku
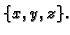 Ako počnemo s
Ako počnemo s
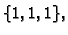 Jacobijeva metoda daje
redom sljedeće aproksimacije.
Jacobijeva metoda daje
redom sljedeće aproksimacije.
Gauss-Seidelova metoda daje
Međutim, ako se promijeni poredak jednadžbi, tako da prva
jednadžba dođe na treće mjesto, druga na prvo, a treća na drugo,
tj. ako sustav napišemo u obliku
onda Jacobijevom metodom dobivamo
a Gauss-Seidelovom
Inače, rješenje na pet decimala točno, je
OR (overrelaxation) metode
Navedene metode se mogu poboljšati, obzirom na konvergentnost i
brzinu konvergencije, na sljedeći način.
Matrica 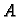 se rastavi kako slijedi
se rastavi kako slijedi
gdje su
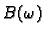 i
i
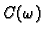 matrice tipa
matrice tipa 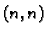 ovisne o
parametru
ovisne o
parametru 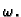 Osim toga
Osim toga
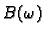 treba biti
regularna. Parametar
treba biti
regularna. Parametar 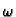 se zove parametar relaksacije. Tada je
se zove parametar relaksacije. Tada je
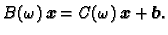 |
(3.11) |
Zbog regularnosti
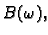 postoji
postoji
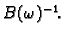 Stavimo
Uvrstimo u (3.11), dobivamo
Iterativni postupak je tada dan formulom
Stavimo
Uvrstimo u (3.11), dobivamo
Iterativni postupak je tada dan formulom
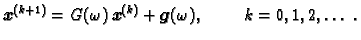 |
(3.12) |
Parametar relaksacije treba odabrati tako da postupak što brže
konvergira.
Jacobijeva OR-metoda (JOR metoda)
Imamo
Neka je 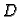 regularna matrica. Stavimo
Tada je
Tako imamo sljedeći algoritam
regularna matrica. Stavimo
Tada je
Tako imamo sljedeći algoritam
Algoritam 9
(Jacobijeva OR-metoda)
Proizvoljno izaberemo početnu aproksimaciju
i zatim računamo sljedeće aproksimacije
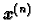
po
formuli
odnosno
gdje je
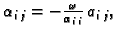
i
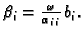
Primijetimo da za
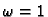 Jacobijeva OR metoda postaje Jacobijeva
metoda.
Jacobijeva OR metoda postaje Jacobijeva
metoda.
Gauss-Seidelova OR-metoda (SOR metoda)
Imamo
Neka je 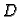 regularna matrica. Stavimo
Tada je
Tako je
Računanje
regularna matrica. Stavimo
Tada je
Tako je
Računanje
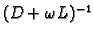 nije jednostavno, pa radimo nešto
drukčije. Polazimo od prethodne jednadžbe
odnosno
Pomnožimo ovu jednadžbu s
nije jednostavno, pa radimo nešto
drukčije. Polazimo od prethodne jednadžbe
odnosno
Pomnožimo ovu jednadžbu s
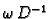 Tako imamo
sljedeći algoritam
Tako imamo
sljedeći algoritam
Algoritam 10
(Gauss-Seidelova OR-metoda)
Proizvoljno izaberemo početnu aproksimaciju
i zatim računamo sljedeće aproksimacije
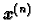
po
formuli
odnosno
gdje je
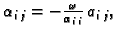
i
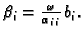
Primijetimo da za
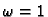 SOR metoda postaje Gauss-Seidelova
metoda.
SOR metoda postaje Gauss-Seidelova
metoda.
Broj 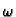 treba uzeti tako da je
treba uzeti tako da je
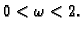 Optimalna
vrijednost ovisi o konkretnom problemu koji se rješava.
Optimalna
vrijednost ovisi o konkretnom problemu koji se rješava.
Primjer 3.11
Riješiti sustav u primjeru
3.10 OR metodama.
Rješenje. Jacobijeva OR metoda ne daje ništa bolje rezultate kad se uzme
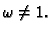 Gauss-Seidelova OR metoda za
Gauss-Seidelova OR metoda za
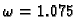 daje
daje
Konvergencija iterativne metode
Iterativni postupci, koje smo upravo definirali, opisani su formulom
gdje je 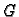 matrica tipa
matrica tipa 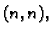 definirana od slučaja do slučaja
na različite načine pomoću matrice
definirana od slučaja do slučaja
na različite načine pomoću matrice 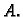 Razmotrimo sada probleme
konvergencije navedenih metoda.
Razmotrimo sada probleme
konvergencije navedenih metoda.
Definicija 16
Neka je
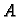
simetrična matrica. Kažemo da je
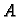 pozitivno definitna
pozitivno definitna, ako vrijedi
Lema 3
Neka je
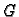
simetrična pozitivno definitna matrica tipa
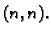
Tada su vlastite vrijednosti
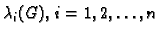
od
matrice
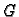
pozitivne, i vrijedi
za svaki
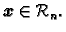
Dokaz. Budući da je matrica 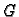 simetrična, postoji
simetrična, postoji 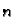 međusobno okomitih i jediničnih vektora
međusobno okomitih i jediničnih vektora
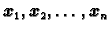 u
u
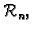 i brojevi
i brojevi
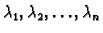 takvih, da je
takvih, da je
Zbog pozitivne definitnosti
Dokažimo sada drugu tvrdnju. Primijetimo
najprije da vlastiti vektori
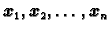 matrice
matrice
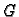 čine ortonormiranu bazu u
čine ortonormiranu bazu u
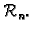 To znači da se bilo koji vektor
To znači da se bilo koji vektor
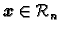 može prikazati kao njihova linearna
kombinacija.
Zbog linearnosti djelovanja matrice
može prikazati kao njihova linearna
kombinacija.
Zbog linearnosti djelovanja matrice 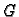 na vektore
Tako je
Odatle
na vektore
Tako je
Odatle
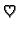
Teorem 25
Neka je
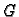
simetrična, pozitivno definitna matrica. Iterativni postupak
konvergira za bilo koju početnu aproksimaciju
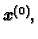
ako i samo ako je
Dokaz. 1. Dokažimo najprije da iz
slijedi konvergencija iterativnog postupka. Doista
i odatle
Odatle možemo, na isti način kao kod računanja apriorne ocjene
greške kod metode iteracije (v. 3.2.2), zaključiti
Budući da je 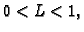 pa niz
pa niz
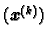 konvergira. Neka je
Tada je
i prema tome niz konvergira k rješenju
konvergira. Neka je
Tada je
i prema tome niz konvergira k rješenju
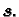
2. Dokažimo obrat, tj. da iz konvergencije postupka slijedi
Iz
i
slijedi
Zbog pretpostavke
slijedi
Ako se to događa za svaku početnu aproksimaciju
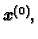 onda mora biti
Budući da je
onda mora biti
Budući da je 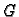 simetrična matrica, ona se može dijagonalizirati,
tj. postoji regularna matrica
simetrična matrica, ona se može dijagonalizirati,
tj. postoji regularna matrica 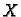 takva, da vrijedi
takva, da vrijedi
![% latex2html id marker 39275
$\displaystyle G^k = X\,\left[\begin{array}{cccc}
...
...ddots & \vdots \\
0 & 0 & \cdots & \lambda_n^k(G)
\end{array}\right]\,X^{-1},$](img2871.gif)
za
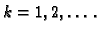
Odatle
Ako pomnožimo s lijeva s 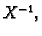 i s desna s
i s desna s 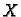 , slijedi
Prema tome
Zbog
, slijedi
Prema tome
Zbog
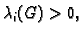 to je moguće samo ako je
to je moguće samo ako je
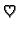
Na isti način kao kod metode iteracije prilikom traženja
nultočke funkcije možemo naći apriornu ocjenu greške
i aposteriornu ocjenu greške
Ovi rezultati su dobiveni uz pretpostavku da je 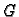 simetrična
pozitivno definitna matrica. To je važan slučaj, koji se pojavljuje
prilikom približnog rješavanja rubnih i rubno-početnih problema
varijacijskim metodama. Međutim, može se dogoditi da
simetrična
pozitivno definitna matrica. To je važan slučaj, koji se pojavljuje
prilikom približnog rješavanja rubnih i rubno-početnih problema
varijacijskim metodama. Međutim, može se dogoditi da 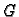 ne
ispunjava ovaj uvjet. Ipak, dobiveni rezultati vrijede i tada uz neke
modifikacije.
ne
ispunjava ovaj uvjet. Ipak, dobiveni rezultati vrijede i tada uz neke
modifikacije.
Prije svega, budući da u općem slučaju vlastite vrijednosti mogu
biti kompleksni brojevi, broj
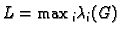 više nema
smisla, jer u skupu kompleksnih brojeva nemamo prirodni
uređaj. Umjesto toga imamo ovu definiciju.
više nema
smisla, jer u skupu kompleksnih brojeva nemamo prirodni
uređaj. Umjesto toga imamo ovu definiciju.
Definicija 17
Neka je
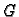
matrica tipa
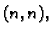
i neka su
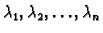
njezine vlastite
vrijednosti. Broj
se zove
spektralni radius matrice
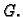
Očito je u slučaju simetričnosti i pozitivne definitnosti matrice
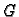
Može se dokazati sljedeći teorem
Teorem 26
Iterativni postupak
konvergira za bilo koju početnu aproksimaciju
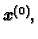
ako i samo ako je
Tako se problem konvergencije iterativnog postupka svodi na problem
ocjene spektralnog radiusa, odnosno najveće po modulu (apsolutnoj
vrijednosti) vlastite vrijednosti matrice, i to ocjene odozgo. Ima
raznih ocjena te vrste. Navedimo neke od njih. Neka je
![$ G=[g_{i\,j}].$](img2886.gif) Tada vrijedi
Tada vrijedi
- 1.
-
![$ \nu(G)\leqslant
\left[\sum_{i=1}^n\sum_{j=1}^n\vert g_{ij}\vert^2\right]^{\frac{1}{2}},$](img2887.gif)
- 2.
-
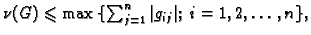
- 3.
-
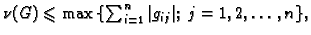
Ako je bilo koji od ovih brojeva na desnoj strani manji od 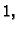 spektralni radius je nužno manji od
spektralni radius je nužno manji od 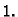 Naglasimo da se ovdje ne
radi o spektralnom radiusu matrice
Naglasimo da se ovdje ne
radi o spektralnom radiusu matrice 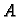 već matrice
već matrice 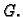
Primjer 3.12
Ispitati konvergenciju Jacobijeve i Gauss-Seidelove metode u
primjeru
3.10.
Rješenje. Kod Jacobijeve metode imamo
a kod Gauss-Seidelove
Matrica sustava, kako je na početku napisan, je
Ako primijenimo Jacobijevu metodu, imamo
Vlastite vrijednosti su
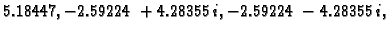
pa je spektralni radius
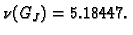
Kod Gauss-Seidelove metode imamo još lošiji rezultat
Vlastite vrijednosti su
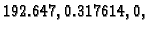
pa je spektralni radius
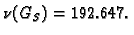
Kad prvu jednadžbu stavimo na treće mjesto, Jacobijeva metoda daje
vlastite vrijednosti su
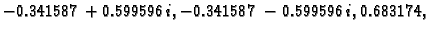
pa je spektralni radius
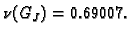
vlastite vrijednosti su
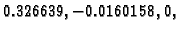
pa je spektralni radius
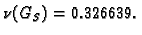
Ako se radi Gauss-Seidelovom OR metodom,
spektralni radius postaje
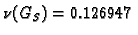
za
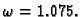
Primjer 3.13
Neka je matrica sustava
Treba ispitati da li Jacobijev i Gauss-Seidelov postupak konvergiraju.
Rješenje. U Jacobijevom postupku je
Njezine vlastite vrijednosti su
spektralni radius je
i prema tome Jacobijeva metoda konvergira za svaku početnu
aproksimaciju.
Kod Gauss-Seidelove metode je
Njezine vlastite vrijednosti su
spektralni radius je sada
pa prema tome Gauss-Seidelova metoda također konvergira za svaku
početnu aproksimaciju, i to brže nego Jacobijeva.
S porastom reda matrice, uz isti tridijagonalni oblik, vlastite
vrijednosti matrice 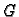 rastu prema
rastu prema 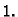 U slučajevima kad su vrlo
blizu broju
U slučajevima kad su vrlo
blizu broju 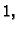 OR metode postaju vrlo efikasne u smislu brzine
konvergencije.
OR metode postaju vrlo efikasne u smislu brzine
konvergencije.




Next: Aproksimacija funkcije i numerička
Up: Numerička matematika
Previous: Rješavanje jednadžbi
Contents
Index
Salih Suljagic
1999-12-17
![\begin{displaymath}
% latex2html id marker 38749
A = \left[
\begin{array}{cccc}
...
...n{array}{c}
x_1 \\ x_2 \\ \vdots \\ x_n
\end{array}\right].\end{displaymath}](img2719.gif)
![]() Nadalje, matrica
Nadalje, matrica ![]() mora biti
regularna i relativno jednostavna, da bismo imali rješenje i da bismo
ga mogli relativno jednostavno izračunati. Također postupak nas mora
približavati k rješenju, tj. postupak mora biti takav da
mora biti
regularna i relativno jednostavna, da bismo imali rješenje i da bismo
ga mogli relativno jednostavno izračunati. Također postupak nas mora
približavati k rješenju, tj. postupak mora biti takav da
![]() različiti od nule (ako je potrebno, premještanjem redaka u
regularnoj matrici se to uvijek može postići).
Rastavimo
različiti od nule (ako je potrebno, premještanjem redaka u
regularnoj matrici se to uvijek može postići).
Rastavimo ![]() kako slijedi
kako slijedi
![\begin{displaymath}
% latex2html id marker 38786
L = \left[
\begin{array}{ccccc}...
...{n\,1} & a_{n\,2} & \cdots & a_{n\,n-1} & 0
\end{array}\right],\end{displaymath}](img2729.gif)
![\begin{displaymath}
% latex2html id marker 38788
D = \left[
\begin{array}{cccc}
...
...0 & a_{n-1\,n} \\
0 & 0 & \cdots & 0 & 0
\end{array}\right].\end{displaymath}](img2730.gif)
![% latex2html id marker 38813
$\displaystyle \boldsymbol{x}^{(0)}=\left[
\begin{array}{c}
x_1^{(0)} \\ x_2^{(0)} \\ \vdots \\ x_n^{(0)}
\end{array}\right],$](img2737.gif)
![]() poželjno je, ako je to moguće, poredati retke u matrici
poželjno je, ako je to moguće, poredati retke u matrici ![]() (jednadžbe
u sustavu) tako da svaki element na glavnoj dijagonali bude po apsolutnoj
vrijednosti veći od sume apsolutnih vrijednosti ostalih elemenata u
retku u kojem se nalazi.
(jednadžbe
u sustavu) tako da svaki element na glavnoj dijagonali bude po apsolutnoj
vrijednosti veći od sume apsolutnih vrijednosti ostalih elemenata u
retku u kojem se nalazi.
![% latex2html id marker 38847
$\displaystyle \boldsymbol{x}^{(k)}=\left[
\begin{array}{c}
x_1^{(k)} \\ x_2^{(k)} \\ \vdots \\ x_n^{(k)}
\end{array}\right]$](img2748.gif)
![% latex2html id marker 38901
$\displaystyle \boldsymbol{x}^{(0)}=\left[
\begin{array}{c}
x_1^{(0)} \\ x_2^{(0)} \\ \vdots \\ x_n^{(0)}
\end{array}\right],$](img2762.gif)
![]() Ako počnemo s
Ako počnemo s
![]() Jacobijeva metoda daje
redom sljedeće aproksimacije.
Jacobijeva metoda daje
redom sljedeće aproksimacije.
![]() se rastavi kako slijedi
se rastavi kako slijedi
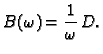
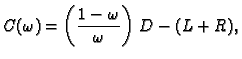
![% latex2html id marker 39048
$\displaystyle \boldsymbol{x}^{(0)}=\left[
\begin{array}{c}
x_1^{(0)} \\ x_2^{(0)} \\ \vdots \\ x_n^{(0)}
\end{array}\right],$](img2808.gif)
![]() Jacobijeva OR metoda postaje Jacobijeva
metoda.
Jacobijeva OR metoda postaje Jacobijeva
metoda.
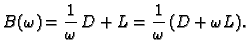
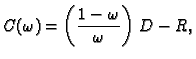
![$\displaystyle \frac{1}{\omega{}}\,(D +
\omega{}L)\,\boldsymbol{x}^{(k+1)} =
\le...
...omega{}}{\omega{}}\right)\,D -
R\right]\,\boldsymbol{x}^{(k)} + \boldsymbol{b}.$](img2825.gif)
![% latex2html id marker 39109
$\displaystyle \boldsymbol{x}^{(0)}=\left[
\begin{array}{c}
x_1^{(0)} \\ x_2^{(0)} \\ \vdots \\ x_n^{(0)}
\end{array}\right],$](img2828.gif)
![]() SOR metoda postaje Gauss-Seidelova
metoda.
SOR metoda postaje Gauss-Seidelova
metoda.
![]() treba uzeti tako da je
treba uzeti tako da je
![]() Optimalna
vrijednost ovisi o konkretnom problemu koji se rješava.
Optimalna
vrijednost ovisi o konkretnom problemu koji se rješava.
![]() Gauss-Seidelova OR metoda za
Gauss-Seidelova OR metoda za
![]() daje
daje
![]() simetrična, postoji
simetrična, postoji ![]() međusobno okomitih i jediničnih vektora
međusobno okomitih i jediničnih vektora
![]() u
u
![]() i brojevi
i brojevi
![]() takvih, da je
takvih, da je
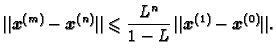
![% latex2html id marker 39275
$\displaystyle G^k = X\,\left[\begin{array}{cccc}
...
...ddots & \vdots \\
0 & 0 & \cdots & \lambda_n^k(G)
\end{array}\right]\,X^{-1},$](img2871.gif) za
za ![% latex2html id marker 39278
$\displaystyle \lim_{k\rightarrow{}\infty{}} G^k= \...
...dots & \vdots \\
0 & 0 & \cdots & \lambda_n^k(G)
\end{array}\right]\,X^{-1} =$](img2872.gif)
![% latex2html id marker 39280
$\displaystyle = X\,\left(\lim_{k\rightarrow{}\inft...
...vdots \\
0 & 0 & \cdots & \lambda_n^k(G)
\end{array}\right]\right)\,X^{-1} = $](img2873.gif)
![% latex2html id marker 39282
$\displaystyle = X\,
\left[\begin{array}{cccc}
\li...
...s & \lim_{k\rightarrow{}\infty{}}\lambda_n^k(G)
\end{array}\right]\,X^{-1} = O.$](img2874.gif)
![% latex2html id marker 39288
$\displaystyle \left[\begin{array}{cccc}
\lim_{k\r...
... & \cdots & \lim_{k\rightarrow{}\infty{}}\lambda_n^k(G)
\end{array}\right] = O.$](img2875.gif)
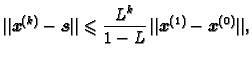
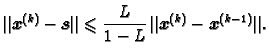
![]() simetrična
pozitivno definitna matrica. To je važan slučaj, koji se pojavljuje
prilikom približnog rješavanja rubnih i rubno-početnih problema
varijacijskim metodama. Međutim, može se dogoditi da
simetrična
pozitivno definitna matrica. To je važan slučaj, koji se pojavljuje
prilikom približnog rješavanja rubnih i rubno-početnih problema
varijacijskim metodama. Međutim, može se dogoditi da ![]() ne
ispunjava ovaj uvjet. Ipak, dobiveni rezultati vrijede i tada uz neke
modifikacije.
ne
ispunjava ovaj uvjet. Ipak, dobiveni rezultati vrijede i tada uz neke
modifikacije.
![]() više nema
smisla, jer u skupu kompleksnih brojeva nemamo prirodni
uređaj. Umjesto toga imamo ovu definiciju.
više nema
smisla, jer u skupu kompleksnih brojeva nemamo prirodni
uređaj. Umjesto toga imamo ovu definiciju.
![]()
![]() Tada vrijedi
Tada vrijedi
![$ \nu(G)\leqslant
\left[\sum_{i=1}^n\sum_{j=1}^n\vert g_{ij}\vert^2\right]^{\frac{1}{2}},$](img2887.gif)
![]() spektralni radius je nužno manji od
spektralni radius je nužno manji od ![]() Naglasimo da se ovdje ne
radi o spektralnom radiusu matrice
Naglasimo da se ovdje ne
radi o spektralnom radiusu matrice ![]() već matrice
već matrice ![]()
![% latex2html id marker 39354
$\displaystyle A = \left[
\begin{array}{rrr}
1.00 &...
...& 3.72 \\
3.15 & - 0.20 & - 1.97 \\
4.43 & 5.84 & 1.79
\end{array}\right].$](img2892.gif)
![% latex2html id marker 39356
$\displaystyle G_J = \left[\begin{array}{rrr}
0 & -...
...& -3.72 \\
15.75 & 0 & -9.85 \\
-2.47486 & -3.26257 & 0
\end{array}\right].$](img2893.gif)
![% latex2html id marker 39362
$\displaystyle G_S = \left[\begin{array}{rrr}
0 & -...
...-3.72 \\
0 & -39.5325 & -68.44 \\
0 & 135.189 & 232.497
\end{array}\right].$](img2896.gif)
![% latex2html id marker 39368
$\displaystyle G_J = \left[
\begin{array}{rrr}
0 & ...
...
-0.758562 & 0 & -0.306507 \\
-0.268817 & -0.674731 & 0
\end{array}\right],$](img2899.gif)
![% latex2html id marker 39374
$\displaystyle G_S = \left[
\begin{array}{rrr}
0 & ...
...
0 & -0.0481626 & -0.780909 \\
0 & 0.0154291 & 0.358786
\end{array}\right],$](img2902.gif)
![% latex2html id marker 39385
$\displaystyle A = \left[
\begin{array}{rrrr}
2 & -...
... & 2 & -1 & 0 \\
0 & -1 & 2 & -1 \\
0 & 0 & -1 & 2 \\
\end{array}\right].$](img2907.gif)
![% latex2html id marker 39387
$\displaystyle G = - D^{-1}(L+R) = \left[
\begin{ar...
... & 1/2 & 0 \\
0 & 1/2 & 0 & 1/2 \\
0 & 0 & 1/2 & 0 \\
\end{array}\right].$](img2908.gif)
![% latex2html id marker 39393
$\displaystyle G = -(L + D)^{-1}\,R = \left[
\begin...
...& 0 \\
0 & 1/8 & 1/4 & 1/2 \\
0 & 1/16 & 1/8 & 1/4 \\
\end{array}\right].$](img2911.gif)
![]() rastu prema
rastu prema ![]() U slučajevima kad su vrlo
blizu broju
U slučajevima kad su vrlo
blizu broju ![]() OR metode postaju vrlo efikasne u smislu brzine
konvergencije.
OR metode postaju vrlo efikasne u smislu brzine
konvergencije.