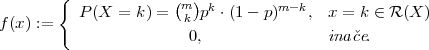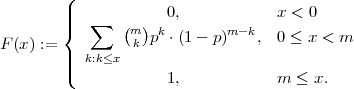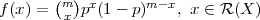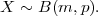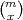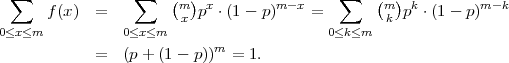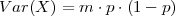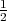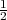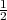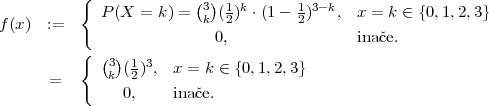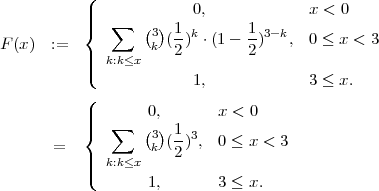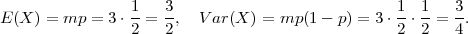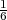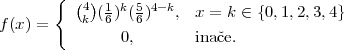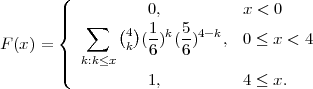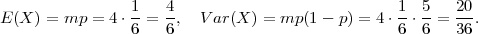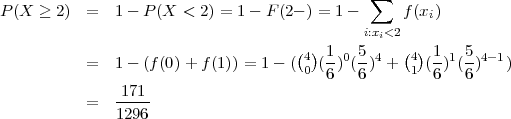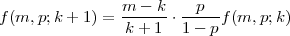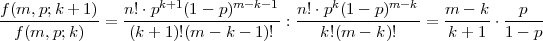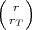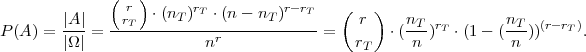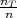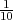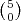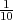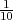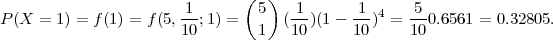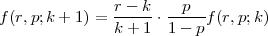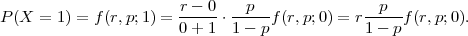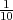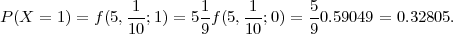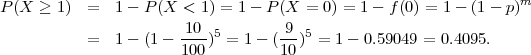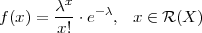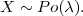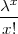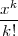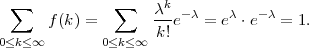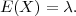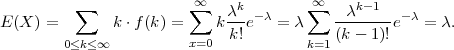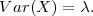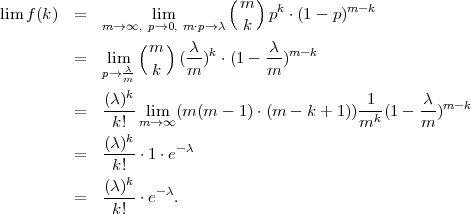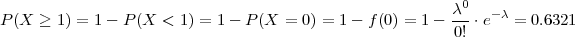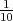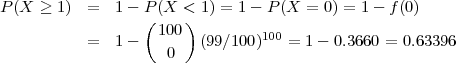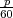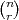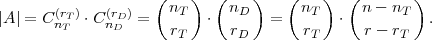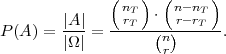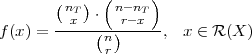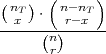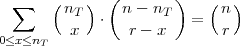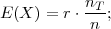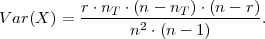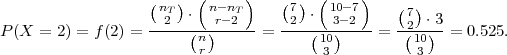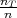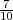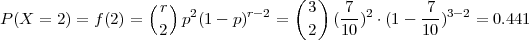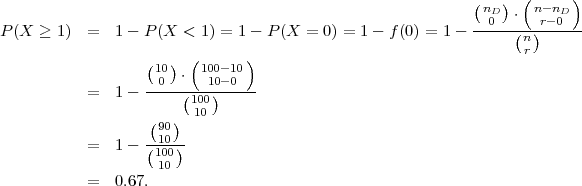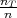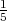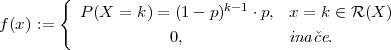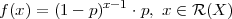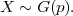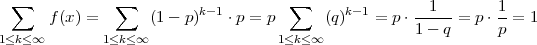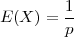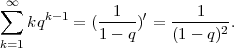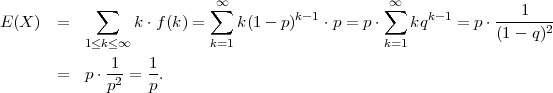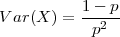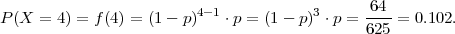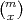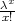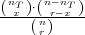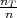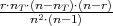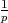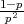Poglavlje 6
PRIMJERI DISKRETNIH
SLUČAJNIH VARIJABLI
U ovom poglavlju istaknut ćemo diskretne slučajne varijable koje se pojavljuju u
odredenim ”scenarijima” i njihove funkcije vjerojatnosti definirat će se kao specifične
distribucije (razdiobe): binomna, Poissonova, hipergeometrijska, geometrijska. Binomna
distribucija vezana je uz scenario Bernoullijeve sheme, Poissonova je granični slučaj
binomne, hipergeometrijska distribucija odgovara uzorku bez vraćanja, a scenario u
kome se broje pokušaji dok se ne dogodi željeni dogadaj prati geometrijska
distribucija.
6.1 Bernoullijeva shema. Binomna
distribucija (razdioba)
MOTIV 6.1
U velikoj kutiji nalazi se p = 10% neispravnih proizvoda. Ako uzmemo uzorak
od r = 5 proizvoda iz kutije (s vraćanjem), slučajna varijabla X = broj neispravnih
proizvoda u uzorku ima binomnu distribuciju X ~ B(r,p). Izračunajte vjerojatnost
(a) da se ne pojavi niti jedan neispravni proizvod,
(b) da se pojavi jedan neispravni proizvod u uzorku,
(c) da se pojavi bar jedan neispravni proizvod u uzorku.
Definicija 6.1 (Bernoullijeva shema)
U m nezavisnih pokusa, vjerojatnost da se dogodi dogadaj A u svakom od njih
je jednaka i P(A) = p. Takvu shemu dogadaja zovemo Bernoullijeva shema.
(Pretpostavljamo da su pokusi nezavisni, tj. da vjerojatnost pojave dogadaja A u
svakom od pokusa ne ovisi od toga da li se on dogodio ili nije u nekom drugom
pokusu.)
Definicija 6.2 (Binomna slučajna varijabla)
Slučajnu varijablu X = broj pojavljivanja dogadaja A u m ∈ ℕ pokusa u
Bernoullijevoj shemi s vjerojatnošću p,p ∈ (0,1) zovemo Binomna slučajna
varijabla.
Specijalno, slučaju samo jednog pokusa m = 1 slučajnu varijablu zovemo Bernoullijeva.
Slika Binomne slučajne varijable je 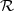 (X) = {0,1,...,m}.
(X) = {0,1,...,m}.
Funkcija vjerojatnosti Binomne slučajne varijable je
Funkcija distribucije Binomne slučajne varijable je
Definicija 6.3 (BINOMNA DISTRIBUCIJA)
Za sve slučajne varijable koje imaju sliku 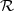 (X) = {0,1,2,...,m} i funkciju
vjerojatnosti
(X) = {0,1,2,...,m} i funkciju
vjerojatnosti
kažemo da imaju BINOMNU DISTRIBUCIJU (RAZDIOBU) s parametrima m i p i
označavamo
PRIMJER 6.1
Funkcija f(x) = 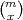 px(1 - p)m-x je funkcija vjerojatnosti.
px(1 - p)m-x je funkcija vjerojatnosti.
Prisjetimo se Binomnog teorema i iskoristimo za računanje
PRIMJER 6.2
Očekivanje diskretne slučajne varijable koja ima binomnu distribuciju X ~ B(m,p)
je
Rješenje:
PRIMJER 6.3
Varijanca diskretne slučajne varijable koja ima binomnu distribuciju X ~ B(m,p)
je
Rješenje: (pokušajte sami)
NAPOMENA 6.1 Ako je p = 1∕2 binomna distribucija je simetrična.
PRIMJER 6.4
Promatramo slučajan pokus gadanja u metu 3 puta. U svakom gadanju
vjerojatnost pogotka mete je 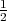 . Neka je slučajna varijabla X = broj pogodaka u
metu. Da li je to slučajna varijabla koja ima binomnu distribuciju? Nadite funkciju
vjerojatnosti i funkciju distribucije slučajne varijable X, očekivanje i varijancu.
. Neka je slučajna varijabla X = broj pogodaka u
metu. Da li je to slučajna varijabla koja ima binomnu distribuciju? Nadite funkciju
vjerojatnosti i funkciju distribucije slučajne varijable X, očekivanje i varijancu.
Rješenje:
To je Bernoullijeva shema dogadaja s m = 3 nezavisna pokusa (ili ponavljamo isti pokus
3 puta nezavisno). Promatramo dogad aj A = pogodak u metu. P(A) = 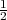 = p u
svakom nezavisnom ponavljanju. Slučajna varijabla
= p u
svakom nezavisnom ponavljanju. Slučajna varijabla
X = broj pojavljivanja dogadaja A (broj uspjeha) ima binomnu distribuciju
X ~ B(m,p) = B(3,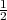 ). Funkcija vjerojatnosti je
). Funkcija vjerojatnosti je
Funkcija distribucije je:
(Do ovih rezultata došli smo i kad smo razmatrali taj primjer slučajne varijable u
prethodnom poglavlju.)
PRIMJER 6.5
Bacamo kocku 4 puta. Neka je slučajna varijabla X = broj šestica. Da li je
to slučajna varijabla koja ima binomnu distribuciju? Nadite funkciju vjerojatnosti
i funkciju distribucije slučajne varijable X, očekivanje i varijancu. Izračunajte
vjerojatnost da su pale bar dvije šestice?
Rješenje:
To je Bernoullijeva shema dogadaja s m = 4 nezavisna pokusa (ili ponavljamo isti pokus
4 puta nezavisno). Promatramo dogadaj A = ”pala je 6”. P(A) = 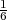 = p u svakom
nezavisnom ponavljanju. Slučajna varijabla X = broj šestica je broj pojavljivanja A
(broj uspjeha) i ona ima binomnu distribuciju X ~ B(m,p) = B(4,
= p u svakom
nezavisnom ponavljanju. Slučajna varijabla X = broj šestica je broj pojavljivanja A
(broj uspjeha) i ona ima binomnu distribuciju X ~ B(m,p) = B(4,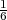 ). Funkcija
vjerojatnosti je
). Funkcija
vjerojatnosti je
Funkcija distribucije je:
Trebamo odrediti P(X ≥ 2).
PRIMJER 6.6 tko želi znati više
Označimo vrijednost funkcije vjerojatnosti f binomne distribucije s parametrima m i
p s f(m,p;k),k ∈{0,1,...,m}. Tada vrijedi rekurzivna relacija
Dokaz: Računamo
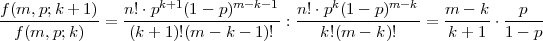
NAPOMENA 6.2
Prisjetimo se primjera za uzorak s vraćanjem.
Slučajni pokus: izbor od r elemenata (s vraćanjem) iz skupa koji ima n elemenata
n = nT + nD, r = rT + rD.
Ω =svi uzorci veličine r iz n-čl. skupa, važan poredak
|Ω| = V n(r) = nr;
Dogadaj A=”uzorak ima rT ispravnih i rD neispravnih”;
|A| =Broj svih uzoraka veličine r iz n -čl. skupa s vraćanjem koji imaju rT
ispravnih i rD neispravnih:
Koristimo formulu za uzorak s vraćanjem |A| = 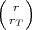 ⋅ (nT )rT ⋅ (n - nT )(r-rT).
⋅ (nT )rT ⋅ (n - nT )(r-rT).
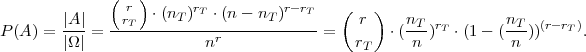 Promatramo slučajnu varijablu X = broj ispravnih predmeta u r članom uzorku iz skupa koji ima n elemenata, od
toga nT ispravnihAko s p =
Promatramo slučajnu varijablu X = broj ispravnih predmeta u r članom uzorku iz skupa koji ima n elemenata, od
toga nT ispravnihAko s p = 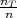 označimo postotak točnih (ispravnih) proizvoda ukupno, onda slučajna
varijabla X = broj ispravnih predmeta u r članom uzorku iz skupa koji ima postotak
p ispravnih elemenata ima binomnu distribuciju s parametrima r i p, X ~ B(r,p).
(Analogno za neispravne elemente)
označimo postotak točnih (ispravnih) proizvoda ukupno, onda slučajna
varijabla X = broj ispravnih predmeta u r članom uzorku iz skupa koji ima postotak
p ispravnih elemenata ima binomnu distribuciju s parametrima r i p, X ~ B(r,p).
(Analogno za neispravne elemente)
PRIMJER 6.7 motiv
U velikoj kutiji nalazi se p = 10% neispravnih proizvoda. Ako uzmemo uzorak
od r = 5 proizvoda iz kutije (s vraćanjem), slučajna varijabla X = broj neispravnih
proizvoda u uzorku ima binomnu distribuciju X ~ B(r,p). Izračunajte vjerojatnost
(a) da se ne pojavi niti jedan neispravni proizvod,
(b) da se pojavi jedan neispravni proizvod u uzorku,
(c) da se pojavi bar jedan neispravni proizvod u uzorku.
Rješenje:
(a) P(X = 0) = f(0) = f(5,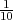 ;0) =
;0) = 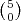 (
(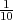 )0(1 -
)0(1 -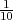 )5 = 0.59049.
)5 = 0.59049.
(b) Možemo računati direktno
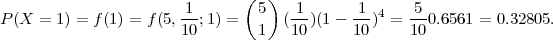
Drugi način je da koristimo rekurzivnu formulu:tko želi znati više
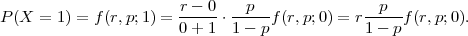 Za
r = 5 i p =
Za
r = 5 i p = 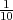
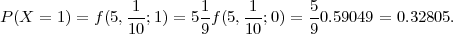
(c)
NAPOMENA 6.3
Ako m → ∞ binomna distribucija teži normalnoj distribuciji (vidi kasnije -
Moivre Laplace teorem).
NAPOMENA 6.4
Ako p → 0 i m →∞ binomna distribucija teži Poissonovoj (vidi Poissonova
distribucija).
6.2 POISSONOVA DISTRIBUCIJA
MOTIV 6.2
Kroz naplatnu kućicu produ prosječno u minuti 2 automobila. Kolika je
vjerojatnost da će u toku bilo koje minute proći
(a) jedan automobil,
(b) barem 3 automobila?
Definicija 6.4 (POISSONOVA DISTRIBUCIJA)
Za diskretnu slučajnu varijablu X koja ima sliku 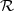 (X) = {0,1,2,..} i funkciju
vjerojatnosti
(X) = {0,1,2,..} i funkciju
vjerojatnosti
kažemo da ima Poissonovu distribuciju s parametrom λ i označavamo
PRIMJER 6.8 Funkcija f(x) = 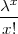 ⋅ e-λ je funkcija vjerojatnosti. Prisjetimo se
razvoja eksponencijalne funkcije u McLaurinov red ex = ∑
0≤x≤∞
⋅ e-λ je funkcija vjerojatnosti. Prisjetimo se
razvoja eksponencijalne funkcije u McLaurinov red ex = ∑
0≤x≤∞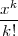 .
.
Računamo
PRIMJER 6.9 Očekivanje diskretne slučajne varijable koja ima Poissonovu
distribuciju X ~ Po(λ) je
Rješenje:
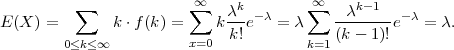
PRIMJER 6.10 Varijanca diskretne slučajne varijable koja ima Poissonovu
distribuciju X ~ Po(λ) je
Rješenje: (Pokušajte sami).
PRIMJER 6.11 Ako u Bernoullijevoj shemi broj m nezavisnih pokusa teži
∞ (jako velik) a vjerojatnost dogadaja A kojeg promatramo u svakom pokusu
teži 0 (jako mala) onda slučajna varijabla X = broj pojavljivanja dogadaja
A ima binomnu distribuciju koju možemo dobro aproksimirati s Poissonovom
distribucijom s parametrom λ = mp, tj. X ~ Po(mp).
Dokaz: tko želi znati višr
Neka je X ~ B(m,p), s parametrima m →∞,p → 0,m ⋅ p → λ.
Računamo graničnu vrijednost funkcije vjerojatnosti binomne distribucije:
Dobili smo funkciju vjerojatnosti Poissonove distribucije za λ = mp.
PRIMJER 6.12 U velikoj kutiji nalazi se p = 1% neispravnih proizvoda. Ako
uzmemo uzorak od r = 100 proizvoda iz kutije, slučajna varijabla X = broj
neispravnih proizvoda u uzorku ima binomnu distribuciju X ~ B(r,p). Budući je
r veliki u odnosu na mali p i r ⋅ p = 1 slučajnu varijablu X možemo aproksimirati
Poissonovom distribucijom X ~ Po(rp). Izračunajte vjerojatnost da se pojavi bar
jedan neispravni proizvod u uzorku.
Rješenje:
Računamo po Poissonovoj distribuciji: X ~ Po(λ), λ = r ⋅ p = 1,
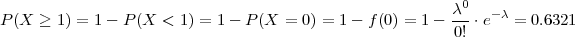
Ako bi računali po binomnoj distribuciji: X ~ B(r,p), r = 100, p = 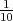 ,
,
Usporedimo li rezultate dobivene vidimo da greška nije velika.
PRIMJER 6.13 Promatramo broj automobila koji produ kroz kontrolnu točku
u intervalima od 1 minute. Neka je p konstantna vjerojatnost da će auto proći u
svakom kratkom intervalu unutar 1 minute ( i pretpostavimo nezavisnost o drugim
dogadajima u tom kratkom vremenu). Slučajna varijabla X = broj automobila koji
produ kroz kontrolnu točku ima Poissonovu distribuciju s parametrom λ = 60⋅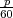 =
p = prosječan broj automobila koji produ kontrolnu točku u 1 minuti, X ~ Po(λ).
=
p = prosječan broj automobila koji produ kontrolnu točku u 1 minuti, X ~ Po(λ).
PRIMJER 6.14 motiv
Kroz naplatnu kućicu produ prosječno u minuti 2 automobila. Kolika je
vjerojatnost da će u toku bilo koje minute proći
(a) jedan automobil,
(b) barem 3 automobila?
Rješenje: Broj automobila koji produ naplatnu kućicu u jednoj minuti ima Poissonovu
distribuciju X ~ Po(λ), λ = 2
(a) P(X = 1) = f(1) = 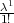 ⋅ e-λ = 2 ⋅ e-2 = 0.27067
⋅ e-λ = 2 ⋅ e-2 = 0.27067
(b)
NAPOMENA 6.5 Poissonova distribucija primjenjuje se u demografiji,
biologiji, fizici, prometu i dr.
6.3 HIPERGEOMETRIJSKA DISTRIBUCIJA
MOTIV 6.3
U velikom pakovanju od 100 cigli distributer garantira da je najviše p = 10%
oštećenih. Kontrolor prihvaća pošiljku samo ako u uzorku od 10 proizvoda iz
pakovanja (bez vraćanja) nema oštećenih. Kolika je vjerojatnost da će kontrolor
odbiti pošiljku?
NAPOMENA 6.6 Prisjetimo se primjera za uzorak bez vraćanja. Slučajni
pokus: izbor od r elemenata (bez vraćanja) iz skupa koji ima n elemenata n =
nT + nD, r = rT + rD.
Ω ={svi uzorci veličine r iz n-čl. skupa}, |Ω| = 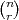 ;
;
Dogadaj A=”uzorak ima rT ispravnih i rD neispravnih”;
|A| =Broj svih uzoraka veličine r iz n -čl. skupa bez vraćanja koji imaju rT
ispravnih i rD neispravnih.
Koristimo formulu za uzorak bez vraćanja:
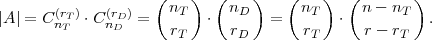
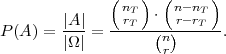
Promatramo slučajnu varijablu X = broj ispravnih predmeta u r-članom uzorku iz
skupa koji ima n elemenata od toga nT ispravnih.
Definicija 6.5 (HIPERGEOMETRIJSKA DISTRIBUCIJA)
Slučajne varijable X koje imaju sliku 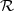 (X) = {0,1,2,..,nT } i funkciju
vjerojatnosti
(X) = {0,1,2,..,nT } i funkciju
vjerojatnosti
gdje su nT ≤ n,r ≤ n,n, nT , r ∈ ℕ kažemo da imaju Hipergeometrijsku distribuciju s
parametrima n, r, nT i označavamo X ~ Hip(n,r,nT ).
PRIMJER 6.15 Funkcija f(x) = 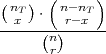 , x ∈
, x ∈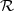 (X) je funkcija
vjerojatnosti.
(X) je funkcija
vjerojatnosti.
Rješenje: Koristimo kombinatorni identitet
PRIMJER 6.16 Slučajnu varijablu X ~ Hip(n,r,nT ) ima očekivanje
i varijancu
PRIMJER 6.17 Slučajni pokus: izbor od r = 3 elemenata (bez vraćanja) iz
skupa koji ima n = 10 elemenata od kojih je nT = 7.
Promatramo slučajnu varijablu X = broj ispravnih predmeta u r članom uzorku iz
skupa koji ima n elemenata, od toga nT ispravnih (bez vraćanja).
(a) Izračunajte vjerojatnost da su u uzorku dva ispravna elementa (točno)?
(b) Izračunajte vjerojatnost da su dva ispravna, ako je uzorak s vraćanjem?
Rješenje:
(a) Uzorak bez vraćanja pa X = broj ispravnih predmeta u r članom uzorku iz skupa
koji ima n elementata od toga nT ispravnih (bez vraćanja) ima hipergeometrijsku
distribuciju X ~ Hip(n,r,nT ). Za n = 10, r = 3, nT = 7, X ~ Hip(10,3,7)
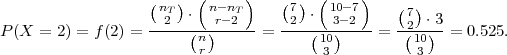 (b)
Uzorak s vraćanjem pa X = broj ispravnih predmeta u r članom uzorku iz skupa koji
ima n elementata od toga nT ispravnih (s vraćanjem) ima binomnu distribuciju
X ~ B(r,p =
(b)
Uzorak s vraćanjem pa X = broj ispravnih predmeta u r članom uzorku iz skupa koji
ima n elementata od toga nT ispravnih (s vraćanjem) ima binomnu distribuciju
X ~ B(r,p = 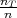 ). Za n = 10, r = 3, nT = 7, X ~ B(3,
). Za n = 10, r = 3, nT = 7, X ~ B(3,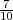 )
)
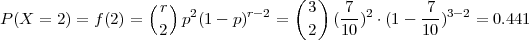
PRIMJER 6.18 motiv
U velikom pakovanju od 100 cigli distributer garantira da je najviše p = 10%
oštećenih. Kontrolor prihvaća pošiljku samo ako u uzorku od 10 proizvoda iz
pakovanja (bez vraćanja) nema oštećenih. Kolika je vjerojatnost da će kontrolor
odbiti pošiljku?
Rješenje:
Uzorak bez vraćanja pa X = broj neispravnih predmeta u r članom uzorku iz skupa
koji ima n elementata od toga nD neispravnih (bez vraćanja) ima hipergeometrijsku
distribuciju X ~ Hip(n,r,nD). Za n = 100, r = 10, nD = 10, X ~ Hip(100,10,10)
Vjerojatnost da će kontolor odbiti pošiljku je 0.67.
NAPOMENA 6.7 Ako je n,nT ,n-nT veliki u odnosu na r onda nije važno je
li uzorak s vraćanjem ili bez vraćanja i Hip(n,r,nT ) distribucija teži B(r,p = 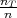 ).
).
Ako je uzorak iz nepoznato velike populacije možemo opet koristiti binomnu
distribuciju bez obzira na vraćanje.
6.4 GEOMETRIJSKA DISTRIBUCIJA
MOTIV 6.4
Student izlazi na ispit dok ga ne položi. Ako je vjerojatnost polaganja ispita
svaki put jednaka p = 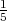 , (jer je student naučio petinu gradiva) kolika je vjerojatnost
da će student 4 puta izlaziti na ispit dok ga ne položi?
, (jer je student naučio petinu gradiva) kolika je vjerojatnost
da će student 4 puta izlaziti na ispit dok ga ne položi?
Definicija 6.6 (Geometrijska slučajna varijabla)
Slučajnu varijablu X = broj ponavljanja pokusa (nezavisnih) dok se ne
dogodi dogadaj A čija je vjerojatnost p ∈ (0,1), zovemo geometrijska slučajna
varijabla.
Slika geometrijske slučajne varijable je 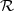 (X) = {1,2,...}.
(X) = {1,2,...}.
Funkcija vjerojatnosti Binomne slučajne varijable je
Definicija 6.7 (GEOMETRIJSKA DISTRIBUCIJA)
Za sve slučajne varijable koje imaju sliku 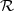 (X) = {1,2,...} i funkciju
vjerojatnosti
(X) = {1,2,...} i funkciju
vjerojatnosti
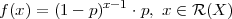 kažemo da imaju GEOMETRIJSKU DISTRIBUCIJU (RAZDIOBU)s parametrom p i označavamo
kažemo da imaju GEOMETRIJSKU DISTRIBUCIJU (RAZDIOBU)s parametrom p i označavamo
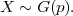
PRIMJER 6.19 Funkcija f(x) = (1 - p)x-1 ⋅ p je funkcija vjerojatnosti.
Prisjetimo se sume geometrijskog reda i iskoristimo za računanje
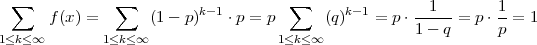
PRIMJER 6.20 Očekivanje diskretne slučajne varijable koja ima geometrijsku
distribuciju X ~ G(p) je
Rješenje:
Prisjetimo se da konvergentan red (npr. geometrijski) možemo derivirati član po član,
pa vrijedi
PRIMJER 6.21 Varijanca diskretne slučajne varijable koja ima geometrijsku
distribuciju X ~ G(p) je
Rješenje: (pokušajte sami)
PRIMJER 6.22 motiv
Student izlazi na ispit dok ga ne položi. Ako je vjerojatnost polaganja ispita
svaki put jednaka p = 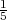 , kolika je vjerojatnost da će student 4 puta izlaziti na ispit
dok ga ne položi?
, kolika je vjerojatnost da će student 4 puta izlaziti na ispit
dok ga ne položi?
Rješenje: X ~ G(p), p = 0.2,
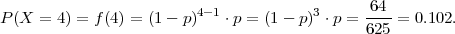
6.5 Ponovimo
BINOMNA DISTRIBUCIJA (RAZDIOBA)
|
|
| binomna distribucija | X ~ B(m,p) |
|
|
| slika binomne sl. var. | 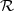 (X) = {0,1,2,...,m} (X) = {0,1,2,...,m} |
|
|
| funkcija vjerojatnosti | f(x) = 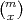 px(1 - p)m-x px(1 - p)m-x |
|
|
| očekivanje | E(X) = mp |
|
|
| varijanca | V ar(X) = mp(1 - p) |
|
|
| |
POISOONOVA DISTRIBUCIJA
|
|
| Poissonova distribucija | X ~ Po(λ) |
|
|
| slika Poissonove sl. var. | 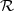 (X) = {0,1,2,...} (X) = {0,1,2,...} |
|
|
| funkcija vjerojatnosti | f(x) = 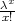 ⋅ e-λ ⋅ e-λ |
|
|
| očekivanje | E(X) = λ |
|
|
| varijanca | V ar(X) = λ |
|
|
| |
HIPERGEOMETRIJSKA DISTRIBUCIJA
|
|
| hipergeometrijska distribucija | X ~ Hip(n,r,nT ) |
|
|
| slika Poissonove sl. var. | 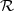 (X) = {0,1,2,..,nT } (X) = {0,1,2,..,nT } |
|
|
| funkcija vjerojatnosti | f(x) = 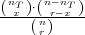 |
|
|
| očekivanje | E(X) = r ⋅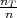 |
|
|
| varijanca | V ar(X) = 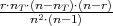 |
|
|
| |
GEOMETRIJSKA DISTRIBUCIJA
|
|
| geometrijska distribucija | X ~ G(p) |
|
|
| slika Poissonove sl. var. | 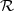 (X) = {1,2,...} (X) = {1,2,...} |
|
|
| funkcija vjerojatnosti | f(x) = (1 - p)x-1 ⋅ p |
|
|
| očekivanje | E(X) = 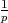 |
|
|
| varijanca | V ar(X) = 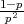 |
|
|
| |
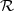 (X) = {0,1,...,m}.
(X) = {0,1,...,m}.