Uvodno o plohama, njihovim tangencijalnim ravninama i normalama

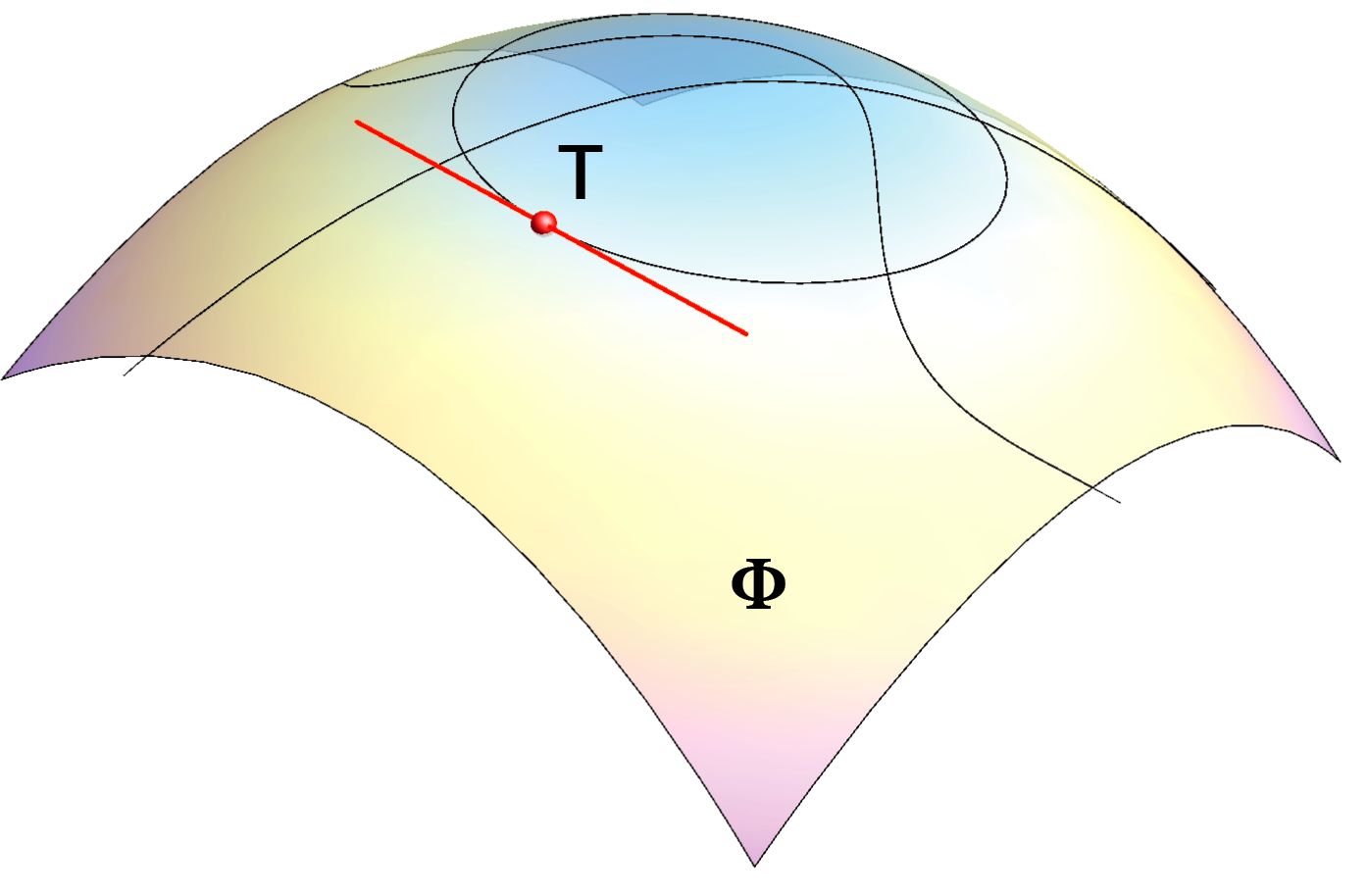
Ploha je skup od \( \infty^2 \) neprekinuto povezanih točaka proširenog euklidskog prostora.

Postoji beskonačno mnogo krivulja (ravninskih i prostornih) koje leže na plohi \(\Phi\).
Nazivamo ih krivuljama ili linijama plohe \(\Phi\).

Za tangentu neke krivulje na plohi s diralištem u točki T, kažemo da je i tangenta plohe u točki T.

Tangencijalna ravnina i normala u regularnoj točki plohe

Svakom točkom plohe prolazi beskonačno mnogo krivulja plohe.

Za neku točku T\(\in\Phi\) promatramo tangente plohe \(\Phi\) kojima je točka T diralište.

  • Za točku plohe kažemo da je regularna ako sve tangente plohe kojima je T diralište leže u jednoj ravnini.

  • Tangencijalna ili dirna ravnina plohe u nekoj njezinoj regularnoj točki T je ravnina koja sadrži sve tangente plohe s diralištem u T, tj.
    tangente s diralištem u T svih onih krivulja plohe koje prolaze točkom T.

  • Normala plohe u nekoj njezinoj regularnoj točki T je pravac koji prolazi točkom T i okomit je na tangencijalnu ravninu plohe u točki T.


    za pokretanje animacije: desni klik na sliku \( \rightarrow \) PLAY





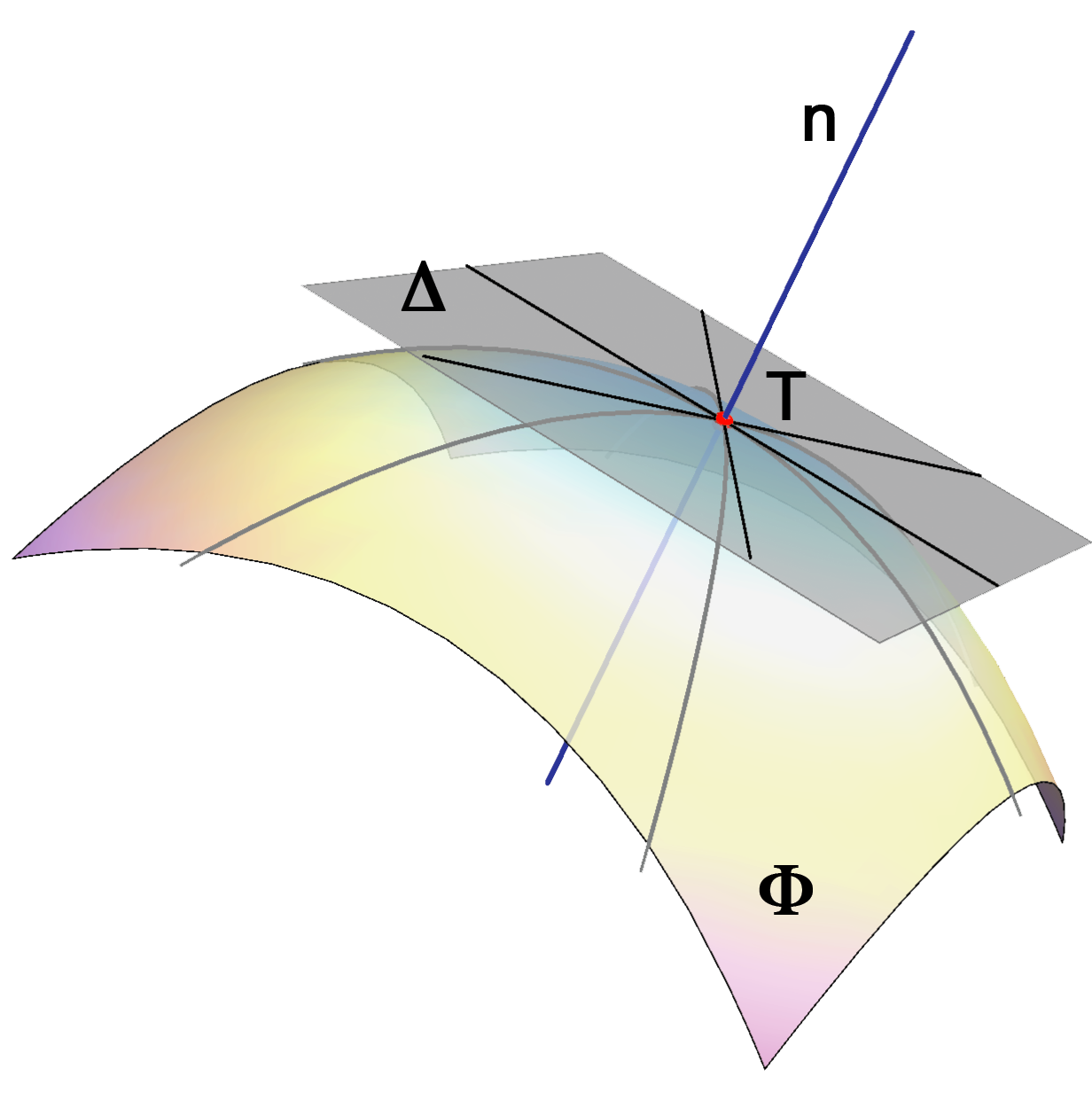
    Tangencijalna ravnina \(\Delta\) i normala n plohe \(\Phi\) u točki T.


    desni klik na sliku \( \rightarrow \) PLAY
    U svakoj regularnoj točki plohe postoje jedinstvena dirna ravnina i normala plohe.
    Dirna ravnina u nekoj točki plohe određena je s bilo koje dvije tangente plohe u toj točki.



    Singularne točke plohe

    S je singularna točka plohe ako tangente plohe, s diralištem u S, ne leže u jednoj ravnini.
    To su npr. točke u kojma ploha samu sebe siječe ili dodiruje.

    U takvim točkama tangente plohe formiraju neki stožac ili dvije ili više ravnina.

    Ako su sve točke neke linije na plohi singularne, onda tu liniju nazivamo singularnom linijom plohe.

    Pravčaste plohe

    Plohu nazivamo pravčastom ako kroz svaku njezinu točku prolazi barem jedan pravac koji cijeli leži na toj plohi.
    Te pravce nazivamo izvodnicama pravčaste plohe.

  • Tangencijalna ravnina u nekoj točki pravčaste plohe uvijek sadrži izvodnicu koja prolazi tom točkom.
    desni klik \( \rightarrow \) PLAY



    Vrste točaka na plohi

  • Točku plohe nazivamo eliptičkom ako se ploha u njezinoj okolini nalazi s iste strane tangencijalne ravnine.

  • Točku plohe nazivamo hiperboličkom ako se ploha u njezinoj okolini nalazi s različitih strana tangencijalne ravnine.
    Smjerove u tangencijalnoj ravnini koji razdvajaju okolinu plohe nazivamo asimptotskim smjerovima plohe u toj točki.

  • Za točku plohe kažemo da je parabolička ako se ploha u njezinoj okolini nalazi s iste strane tangencijalne ravnine,
    ali je ta ravnina tangencijalna i za sve točke neke krivulje na plohi koje leže u promatranoj okolini točke.

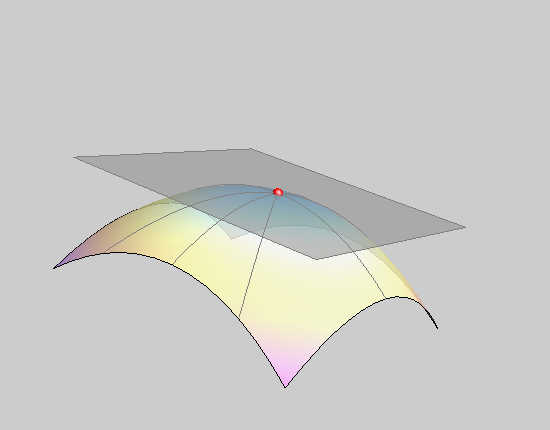
    eliptička točka plohe

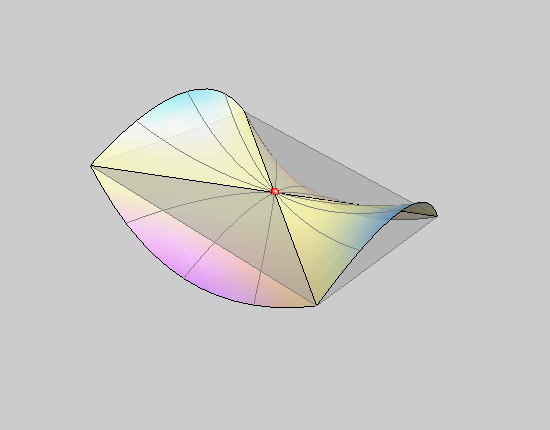
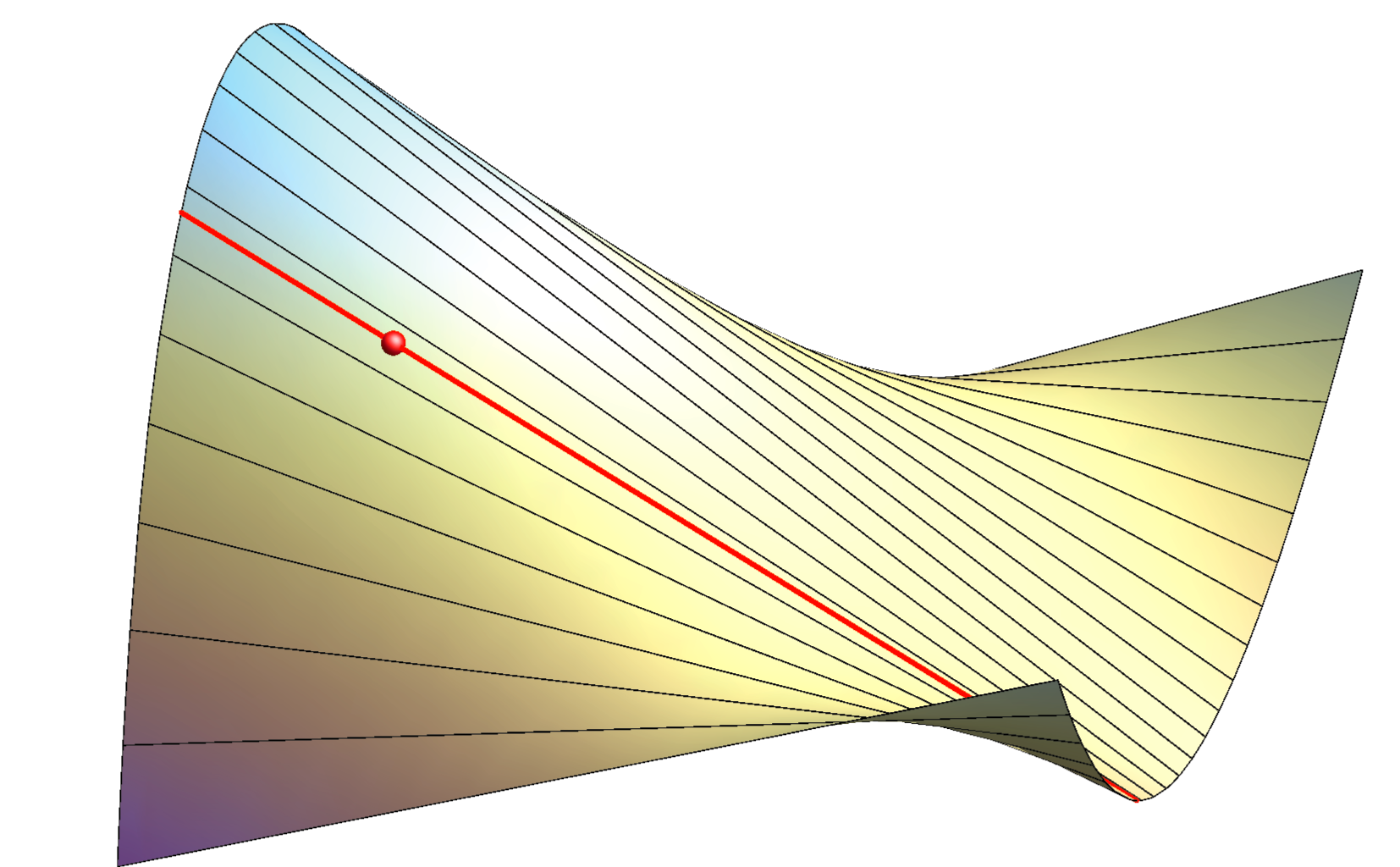
    hiperbolička točka plohe

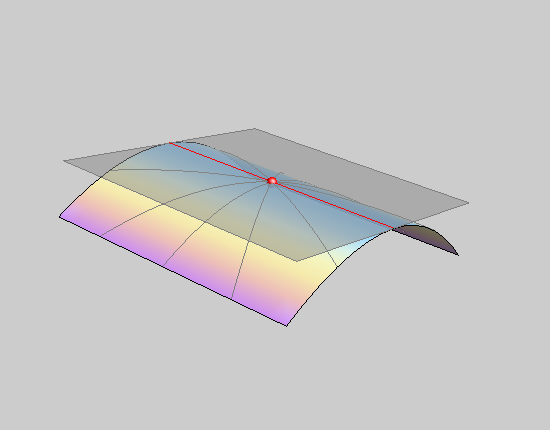
    parabolička točka plohe



  • Plohe kojima su sve točke paraboličke nazivamo jednostruko zakrivljenim plohama.

    Sve takve plohe su pravčaste i duž svake izvodnice imaju jedinstvenu tangencijalnu ravninu.

    Njihovo je svojstvo da se bez istezanja i kidanja mogu razviti u ravninu pa ih nazivamo razvojnim plohama.
    Stošci i valjci su primjeri takvih ploha.

  • Dijelove plohe (ili cijele plohe) koji sadrže samo eliptičke ili samo hiperboličke točke nazivamo dvostruko zakrivljenim dijelovima (ili plohama).

    Za dijelove koji sadrže samo eliptičke točke kažemo da su dvostruko istosmjerno zakrivljeni. Na njima nema pravaca.

    Za dijelove koji sadrže samo hiperboličke točke kažemo da su dvostruko protusmjerno zakrivljeni.
    Ako na takvoj plohi postoji pravac onda tangencijalna ravnina plohe u nekoj točki tog pravca općenito ne dodiruje plohu duž cijelog pravca.

    Dvostruko zakrivljene plohe ne mogu se bez kidanja i istezanja razviti u ravninu, nazivamo ih vitoperim plohama.



    Pojam zakrivljenosti u nekoj točki plohe pripada području diferencijalne geometrije i nadilazi okvire našeg kolegija.
    Ipak, za studente koji se u to (barem na nivou ilustracija) žele malo udubiti evo nekih linkova:
    O zakrivljenosti ravninske krivulje
    O normalnoj zakrivljenosti plohe
    Wolfram Demonstrations Project - rad studentice D. Štambuk
    Rad nagrađen Rektorovom nagradom - S. Hak i M. Uroš


    Sonja Gorjanc - 3DGeomTeh - Razvojni projekt Sveučilišta u Zagrebu