Introduction to Surfaces, Tangent Planes and Normal Lines

A surface is a set of \( \infty^2 \) continuously connected points in the extended euclidean space.
There are infinitely many plane curves and space curves that lie on the surface \(\Phi\).
We call them curves on the surface \(\Phi\).

A line is a tangent of the surface in a point T if it is a tangent line of a curve on the surface with the point of tangency T.

Tangent plane and normal line in a regular point of a surface

There are infinitely many curves of the surface through every point on the surface.

If a point T\(\in\Phi\) is given, observe the tangents of the surface \(\Phi\) that pass through T.

  • A point on the surface is regular if all tangents through T lie in a plane.

  • A tangent plane of the surface in a regular point T of the surface is the plane that contains all tangents of the surface that pass through T, i.e. all tangent lines to a curve on the surface that have T as the point of tangency.

  • A normal line of the surface in a regular point T is a line through T perpendicular to the tangent plane in T.


    to start the animation: right-click on the image \( \rightarrow \) PLAY





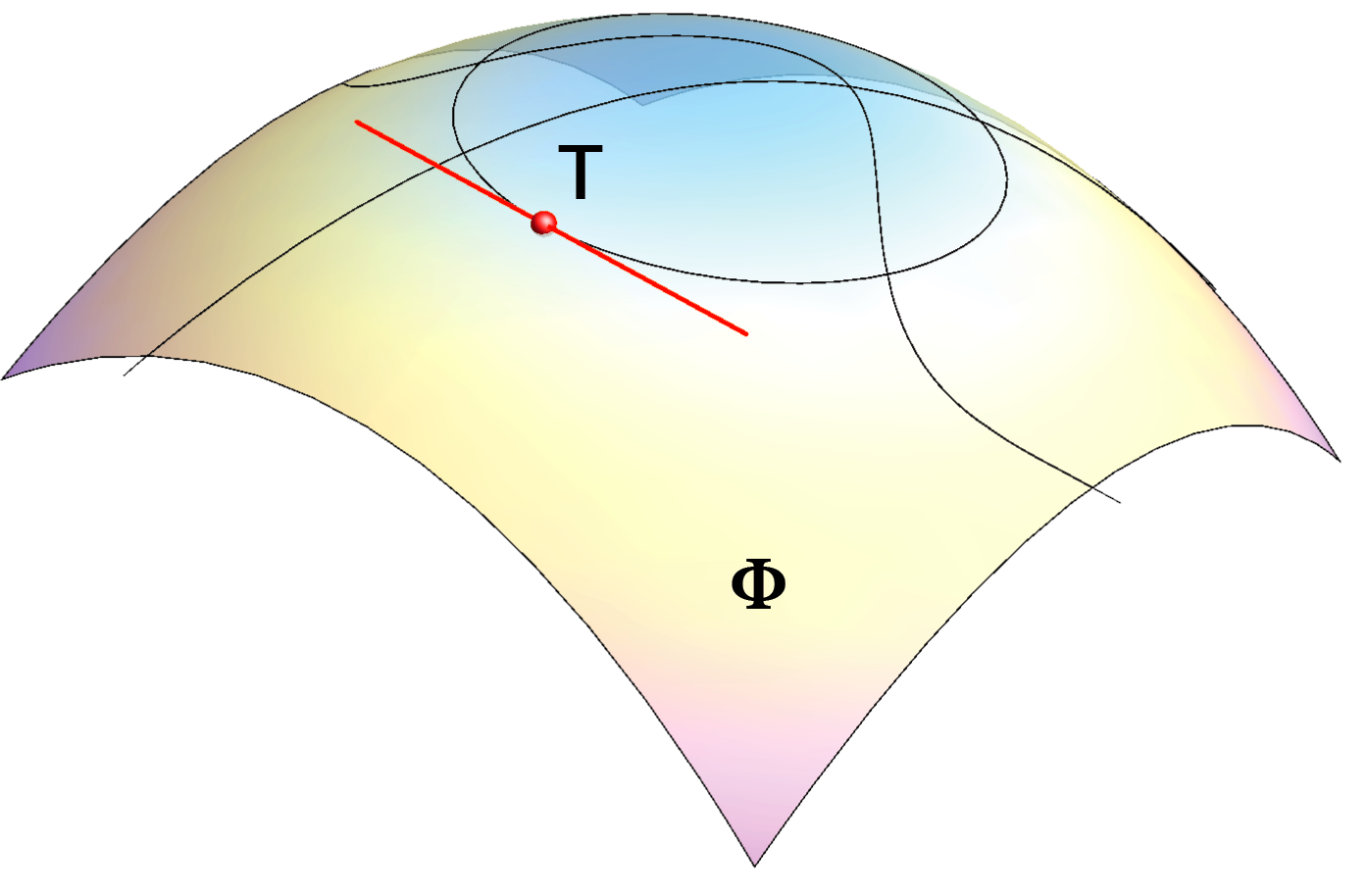
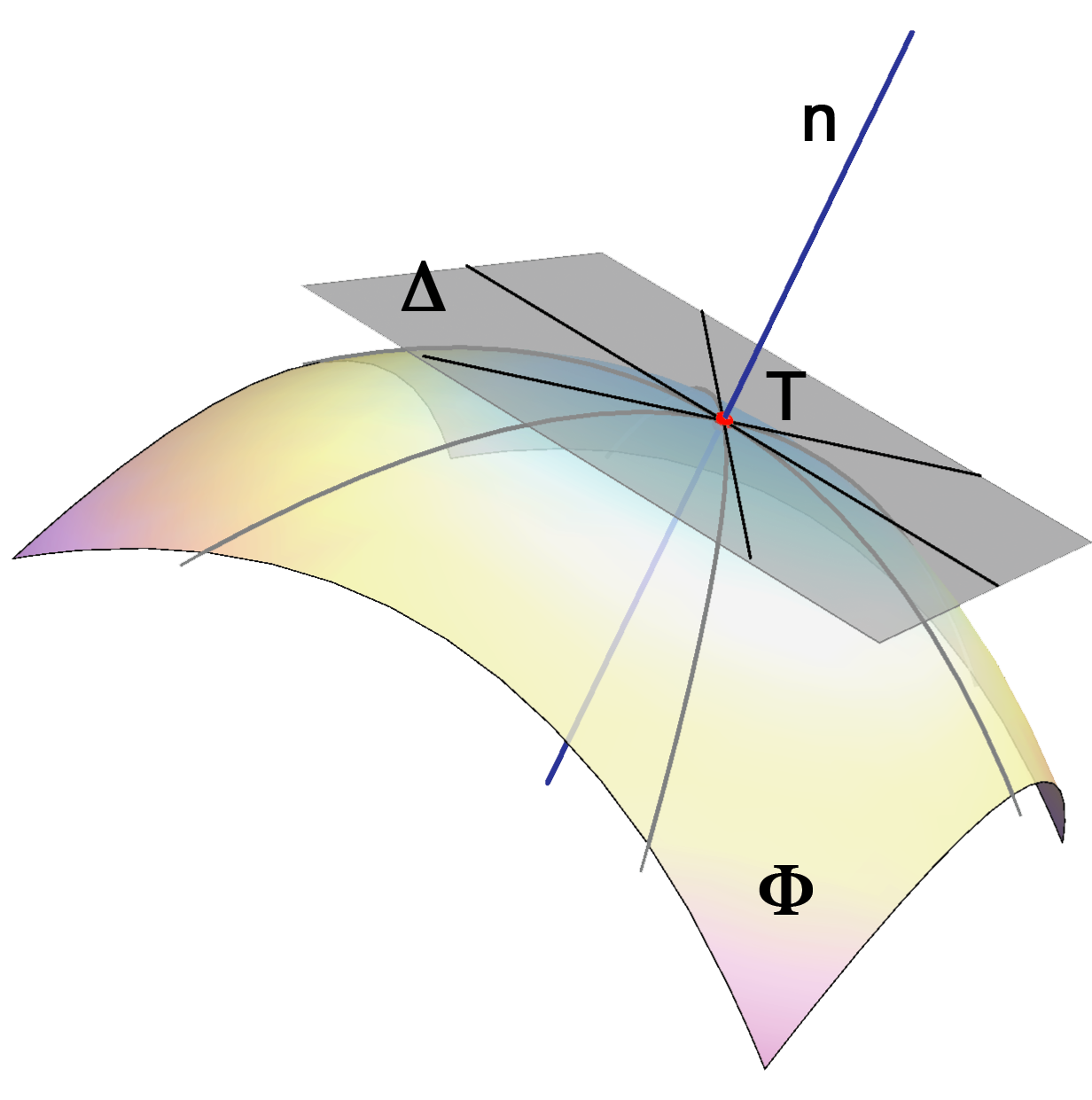
    Tangent plane \(\Delta\) and normal line n of the surface \(\Phi\) in T.


    right-click on the image \( \rightarrow \) PLAY
    There is a unique tangent plane and a normal line at each regular point of a surface.
    The tangent plane is determined by two tangents at a regular point.



    Singular points on the surface

    The point S is a singular point of the surface if tangent lines in the points S do not lie in a plane.
    Such points are for example points in which a surface intersect itself.
    Tangents of a surface at a singular point form a cone or two planes or more.

    If all points of a curve on a surface are singular, such a curve is called a singular curve of the surface.

    Ruled surfaces

    A surface is a ruled surface if there is at least one line that lies on the surface through each point on the surface.
    Such lines are called the rulings of the ruled surface.

  • Tangent plane at a point of the ruled surface always contains rulingspassing through that point.
    right-click \( \rightarrow \) PLAY



    Classification of points of the surface

  • A point of the surface is elliptic if the surface in its neighborhood is on the same side of the tangent plane.

  • A point of the surface is hyperbolic if the surface in its neighborhood is on both sides of the tangent plane.
    Directions in the tangent plane that separate this neighborhood of the point are called asymptotic directions.

  • A point T of the surface is  parabolic  if the surface in its neighborhood  is on the same side of the tangent plane, but this tangent plane is also the tangent plane for all points of some curve of the surface close to the point T.

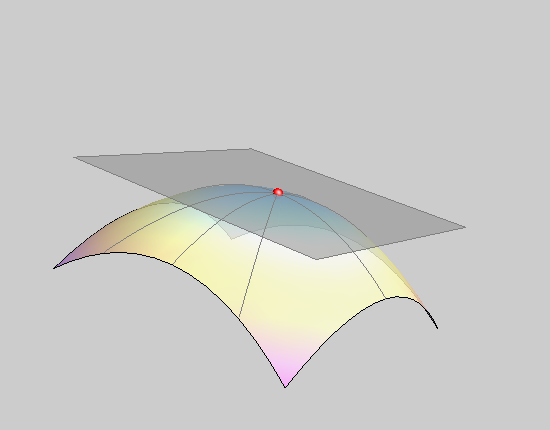
    an elliptic point of the surface

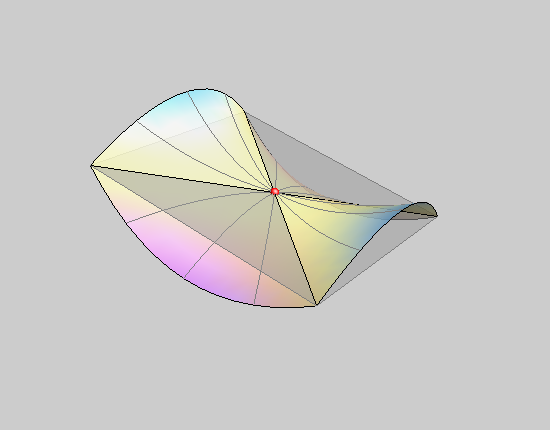
    a hyperbolic point of the surface

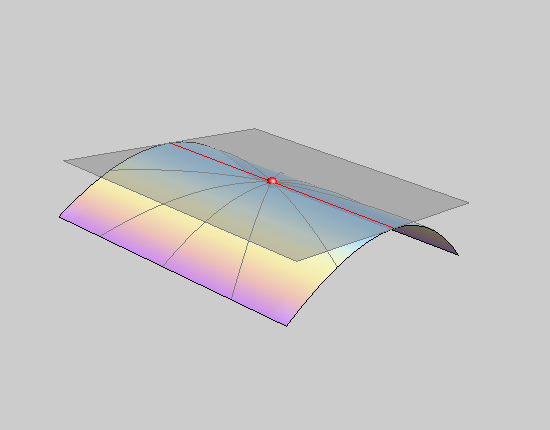
    a parabolic point of the surface


  • All surfaces that contain only parabolic points are ruled surfaces and there is a unique tangent plane along a ruling.

    These surfaces can be obtained from a plane by bending, i.e. they can be flattened onto a plane without distortion - they are called developable surfaces.
    Such surfaces for example are cones and cylinders.

  • Surfaces that contain only elliptic points are called synclastic surfaces. These surfaces do not contain lines.
  • Surfaces that contain only hyperbolic points are called anticlastic surfaces. If they contain a line, then the tangent plane in a point on that line does not contain that line.
  • A surface that contain elliptic and (or) hyperbolic points cannot be obtained from the plane by bending, they are non-developable surfaces and they are often referred to have a double curvature (compound curvature or being  doubly curved).


    A curvature of a surface is a notion from differential geometry and it exceeds the range of this class.
    For those who want to learn some more about curvature:
    Curvature of plane curves
    Normal curvature of the surface
    Wolfram Demonstrations Project - by D. Štambuk
    Student work - by S. Hak i M. Uroš


    Created by Sonja Gorjanc, translated by Helena Halas and Iva Kodrnja - 3DGeomTeh - Developing project of the University of Zagreb