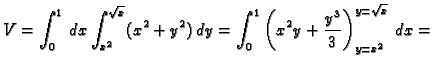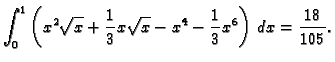



Next: Trostruki integral
Up: Višestruki integrali
Previous: Višestruki integrali
Contents
Index
Subsections
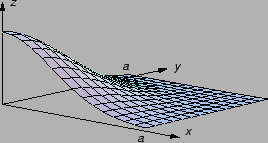
Rub tijela se obično sastoji od ploha, koje su grafovi neprekidnih funkcija
od dvije varijable. Tako se problem volumena tijela može svesti na problem
računanja volumena tijela odozgo omeđenog plohom a odozdo ravninom 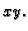 Uzmimo najprije jednostavan slučaj neprekidne funkcije
Uzmimo najprije jednostavan slučaj neprekidne funkcije
![$ f:[a,b]\times [c,d]
\rightarrow R.$](img980.gif) Neka je pravokutnik
Neka je pravokutnik
![$ I=[a,b]\times [c,d]$](img981.gif) u prvom kvadrantu
ravnine
u prvom kvadrantu
ravnine 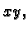 a ploha neka se nalazi u prvom oktantu. Želimo naći volumen
a ploha neka se nalazi u prvom oktantu. Želimo naći volumen
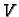 tijela, koje je odozgo omeđeno plohom
tijela, koje je odozgo omeđeno plohom 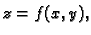 a odozdo pravokutnikom
a odozdo pravokutnikom
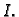
Načinimo subdiviziju
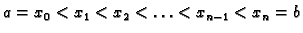 segmenta
segmenta ![$ [a,b]$](img986.gif) i
i
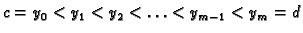 segmenta
segmenta ![$ [c,d].$](img988.gif) Time smo pravokutnik
Time smo pravokutnik
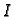 podijelili na podpravokutnike
podijelili na podpravokutnike
![$ I_{ij}=[x_{i-1},x_i]\times [y_{j-1},y_j].$](img989.gif) Neka je
Neka je 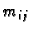 minimalna, a
minimalna, a 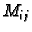 maksimalna vrijednost funkcije
maksimalna vrijednost funkcije 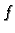 na
na
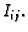 Tada vrijedi
Tada vrijedi
Lijeva dvostruka suma predstavlja sumu volumena upisanih kvadara, a desna
suma predstavlja sumu volumena opisanih kvadara plohi. Tim sumama smo
približno odredili volumen. Očekujemo da ćemo sa sve sitnijim podjelama
dobivati sve bolje aproksimacije volumena 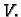 Ova konstrukcija nas vodi na
pojam dvostrukog integrala.
Ova konstrukcija nas vodi na
pojam dvostrukog integrala.
Pretpostavimo da je dana ograničena funkcija 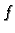 na
na
![$ I=[a,b]\times [c,d].$](img995.gif) Podsjetimo se da ograničenost funkcije znači da je slika funkcije
Podsjetimo se da ograničenost funkcije znači da je slika funkcije
![$ \{f(x,y);\;(x,y)\in [a,b]\times [c,d]\}$](img996.gif) ograničen skup u
ograničen skup u 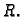
Neka
su 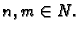 Neka je
subdivizija segmenta
Neka je
subdivizija segmenta ![$ [a,b],$](img1000.gif) a
subdivizija segmenta
a
subdivizija segmenta ![$ [c,d].$](img988.gif) Neka je
Neka je
![$ I_{ij}=[x_{i-1},x_i]\times [y_{j-1},y_j].$](img989.gif)
Slika 2.1:
Podjela pravokutnika inducirana subdivizijom segmenata.
|
|
Ograničenost
funkcije na 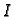 povlači njenu ograničenost na
povlači njenu ograničenost na 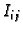 za svaki
za svaki
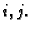 To znači da postoje supremum i infimum skupa
To znači da postoje supremum i infimum skupa
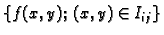 (8.2). Stavimo
Ako je funkcija
(8.2). Stavimo
Ako je funkcija 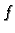 neprekidna na
neprekidna na 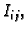 onda se supremum poklapa s
maksimumom, a infimum s minimumom funkcije na
onda se supremum poklapa s
maksimumom, a infimum s minimumom funkcije na 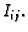 Osim toga, ako
je
Osim toga, ako
je
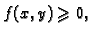 onda je
onda je 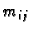 visina maksimalnog upisanog,
a
visina maksimalnog upisanog,
a 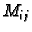 visina minimalnog opisanog kvadra grafu funkcije (dijelu
plohe) nad pravokutnikom
visina minimalnog opisanog kvadra grafu funkcije (dijelu
plohe) nad pravokutnikom 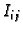 (slika 2.2).
(slika 2.2).
Slika 2.2:
Maksimalni upisani i minimalni opisani kvadar.
|
|
Formirajmo sljedeće sume.
Broj
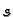 se zove donja Darbouxova suma, a broj
se zove donja Darbouxova suma, a broj 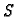 se zove
gornja Darbouxova suma. Ako je
se zove
gornja Darbouxova suma. Ako je 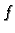 pozitivna funkcija,
onda je
pozitivna funkcija,
onda je 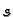 zbroj volumena upisanih kvadara, a
zbroj volumena upisanih kvadara, a 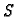 zbroj volumena
opisanih kvadara dobivenih od jedne subdivizije.
zbroj volumena
opisanih kvadara dobivenih od jedne subdivizije.
Neka je
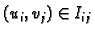 proizvoljan. Broj
proizvoljan. Broj
se zove integralna suma. Zbog očigledne nejednakosti
imamo
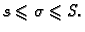 |
(2.1) |
Sve što smo do sada uradili proizašlo je iz jedne subdivizije. Sada
zamislimo sve moguće subdivizije. Svaka od njih daje po jednu donju i
jednu gornju Darbouxovu sumu, i beskonačno mnogo integralnih suma,
ali uvijek vrijedi nejednakost (2.1). Označimo s
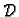 skup svih donjih Darbouxovih suma, a s
skup svih donjih Darbouxovih suma, a s
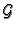 skup svih gornjih Darbouxovih suma. Neka je
skup svih gornjih Darbouxovih suma. Neka je
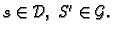 Uzmimo novu subdiviziju, koja sadrži sve točke jedne i
druge subdivizije, i neka su
Uzmimo novu subdiviziju, koja sadrži sve točke jedne i
druge subdivizije, i neka su 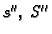 njezina donja i gornja
Darbouxova suma. Tada vrijedi (slika 2.3)
njezina donja i gornja
Darbouxova suma. Tada vrijedi (slika 2.3)
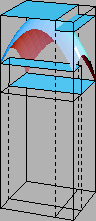
Slika 2.3:
Profinjenjem subdivizije opisani (upisani) kvadar se raspada na dva opisana (upisana) kvadra i time se ukupni volumen opisanih (upisanih) kvadara smanjuje (povećava).
Odatle slijedi da je bilo koja donja Darbouxova suma manja ili jednaka
od bilo koje gornje Darbouxove sume. To znači da je skup
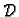 odozgo, a skup
odozgo, a skup
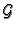 odozdo ograničen, pa prema
tome postoje
odozdo ograničen, pa prema
tome postoje
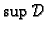 i
i
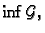 i vrijedi
i vrijedi
Definicija 17
Kažemo da je funkcija
integrabilna ili
Riemann-integrabilna na
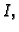
ako je
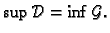
U tom
slučaju broj
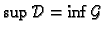
zovemo
dvostrukim integralom funkcije
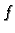
na
![$ I=[a,b]\times [c,d].$](img995.gif)
Pišemo
Funkcija
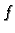
se zove
podintegralna
funkcija, pravokutnik
![$ I=[a,b]\times [c,d]$](img981.gif) područje integracije
područje integracije.
Definicija 18
Neka je
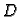
zatvoreno ograničeno područje u
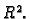
Neka je
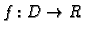
ograničena funkcija na
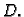
Neka je
![$ I=[a,b]\times [c,d]$](img981.gif)
minimalni pravokutnik koji sadrži
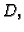
Slika 2.4:
Konveksno područje.
|
|
i neka je
Kažemo da je
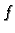 integrabilna na
integrabilna na 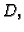
ako je
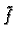
integrabilna
na
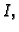
i broj
zovemo
dvostrukim integralom
funkcije 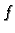 na
na 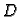
.
- 1.
- Ako su
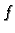 i
i 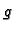 integrabilne funkcije na
integrabilne funkcije na 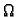 i
i
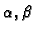 proizvoljni realni brojevi, onda je
proizvoljni realni brojevi, onda je
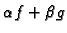 integrabilna na
integrabilna na
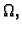 i
i
- 2.
- Ako je
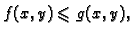 za svaki
za svaki
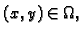 onda je
onda je
- 3.
- Neka je
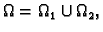 gdje su
gdje su 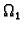 i
i
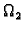 zatvorena područja čiji je presjek krivulja (skup
površine nula). Tada je
zatvorena područja čiji je presjek krivulja (skup
površine nula). Tada je
- 4.
- Ako je
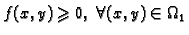 i
i
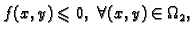 onda formula za
volumen tijela
onda formula za
volumen tijela 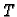 između grafa funkcije i ravnine
između grafa funkcije i ravnine 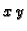 glasi
glasi
- 5.
-
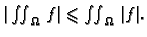
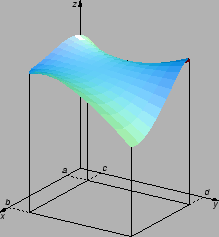
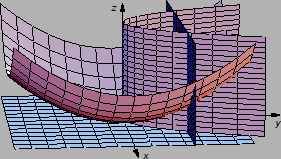
Slika:
Kvadri imaju isti volumen kao dio prostora ispod plohe,
a iznad ravnine 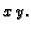 Lijevo je graf neprekidne funkcije, pa
ploha siječe gornju stranicu kvadra, a desno je graf funkcije
koja nije neprekidna, i nema točaka presjeka.
Lijevo je graf neprekidne funkcije, pa
ploha siječe gornju stranicu kvadra, a desno je graf funkcije
koja nije neprekidna, i nema točaka presjeka.
|
|
- 6.
- Teorem srednje vrijednosti
(integralni). Neka
je
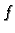 neprekidna funkcija integrabilna na zatvorenom
ograničenom području
neprekidna funkcija integrabilna na zatvorenom
ograničenom području 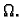 Tada postoji
Tada postoji
 tako da
je
gdje je
tako da
je
gdje je
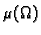 površina područja
površina područja 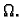
Dokaz. Neprekidna funkcija na zatvorenom
ograničenom području dostiže svoju najmanju i svoju najveću
vrijednost, tj. postoje točke 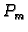 i
i 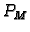 takve da je
za svaki
takve da je
za svaki
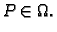 Odatle slijedi
tj.
Osim toga neprekidna funkcija na zatvorenom ograničenom području
dostiže svaku međuvrijednost, što znači da postoji
Odatle slijedi
tj.
Osim toga neprekidna funkcija na zatvorenom ograničenom području
dostiže svaku međuvrijednost, što znači da postoji
 takav da je
takav da je
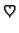
Pretpostavimo da je 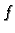 integrabilna na
integrabilna na
![$ I=[a,b]\times [c,d].$](img995.gif) Tada za
proizvoljni
Tada za
proizvoljni
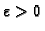 postoji takva subdivizija, da je
postoji takva subdivizija, da je
s točnošću
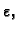 za bilo koju integralnu sumu
za bilo koju integralnu sumu 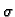 određenu tom
subdivizijom.
određenu tom
subdivizijom.
Doista, budući da je
slijedi da postoji subdivizija takva da je
Također postoji subdivizija takva da je
Subdivizija, koja koristi točke podjele i jedne i druge subdivizije,
daje donju Darbouxovu sumu 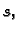 gornju Darbouxovu sumu
gornju Darbouxovu sumu 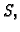 i neku
integralnu sumu
i neku
integralnu sumu 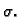 Vrijedi
Odatle
Prema tome integralna suma
Vrijedi
Odatle
Prema tome integralna suma 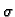 aproksimira
integral funkcije
aproksimira
integral funkcije 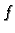 s točnošću
s točnošću
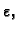 tj.
tj.
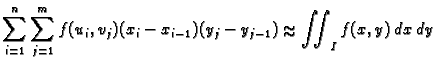 |
(2.2) |
s točnošću
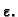
Formulu (2.2) možemo prepisati kao
Na temelju definicije Riemannovog integrala funkcije jedne varijable,
imamo
Tako je
Tako zaključujemo da vrijedi
Slično iz
slijedi
Ove formule imaju veliko praktično značenje, jer se pomoću njih
izračunavanje dvostrukog integrala po pravokutniku svodi na
sukcesivno računanje dva jednostruka integrala.
Ako je još
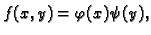 onda se dvostruki integral svodi na
produkt dva jednostruka integrala
onda se dvostruki integral svodi na
produkt dva jednostruka integrala
Računanje po proizvoljnom zatvorenom području
Neka je
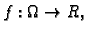 i neka je
i neka je
![$ I=[a,b]\times [c,d]$](img981.gif) minimalni
pravokutnik koji sadrži
minimalni
pravokutnik koji sadrži 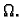 Neka je dalje područje
Neka je dalje područje 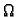 takvo da
se njegov rub sastoji od dvije krivulje, koje su grafovi funkcija od
takvo da
se njegov rub sastoji od dvije krivulje, koje su grafovi funkcija od 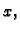 i to donji rub neka je graf funkcije
i to donji rub neka je graf funkcije 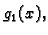 a gornji graf funkcije
a gornji graf funkcije
Slika 2.6:
Računanje dvostrukog integrala.
|
|
Tada je
Slično, ako se rub od 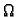 može shvatiti kao dvije krivulje koje su
grafovi funkcija od
može shvatiti kao dvije krivulje koje su
grafovi funkcija od 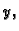 i to lijeva graf od
i to lijeva graf od 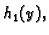 a desna graf od
a desna graf od
Slika 2.7:
Računanje dvostrukog integrala.
|
|
onda vrijedi
Ako nijedno od toga nije ispunjeno, onda se pravokutnik dijeli na manje
pravokutnike na kojima je moguće primijeniti jedno od gornjih pravila.
Slika 2.8:
Računanje dvostrukog integrala.
|
|
Neka je dano tijelo 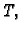 i neka je njegov rub dan plohama koje su
grafovi funkcija
i neka je njegov rub dan plohama koje su
grafovi funkcija 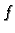 i
i 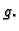 Neka je ploha
Neka je ploha 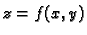 gornji, a ploha
gornji, a ploha
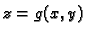 donji rub tijela. Neka su funkcije
donji rub tijela. Neka su funkcije 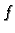 i
i 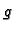 integrabilne.
Tada je formulom
integrabilne.
Tada je formulom
dan volumen tijela 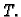
Primjer 2.1
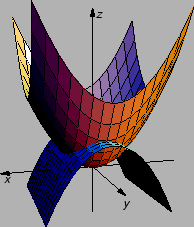
Naći volumen tijela omeđenog plohama
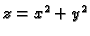
i
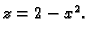
Rješenje.
Presjek ploha je krivulja u prostoru, čiju ćemo
projekciju na ravninu
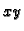
dobiti tako da eliminiramo
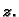
To je ovdje
jednostavno
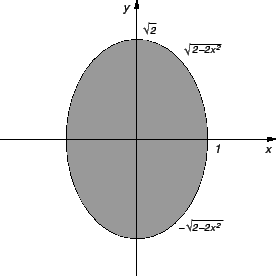
To je jednadžba elipse s poluosima
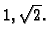
Dio ravnine
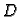
omeđen elipsom je područje po kojem treba
integrirati. Gornji rub tijela čini ploha
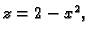
a donji ploha
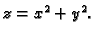
Dakle
Zaključimo problem volumena sljedećom opaskom. Neka je 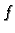 ograničena funkcija na pravokutniku
ograničena funkcija na pravokutniku
![$ I=[a,b]\times [c,d],$](img1107.gif) i neka je
i neka je
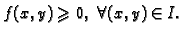 Njezin graf, pravokutnik
Njezin graf, pravokutnik
![$ [a,b]\times [c,d],$](img1109.gif) i ravnine paralelne s osi
i ravnine paralelne s osi 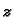 kroz stranice
pravokutnika
kroz stranice
pravokutnika 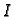 određuju skup, ``tijelo''
određuju skup, ``tijelo'' 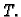 Na temelju do sada
rečenog prirodno je reći da
Na temelju do sada
rečenog prirodno je reći da 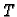 ima
volumen, ako je
ima
volumen, ako je 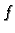 integrabilna na
integrabilna na 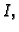 i da je u
tom slučaju volumen od
i da je u
tom slučaju volumen od 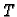 jednak
jednak
Da ima smisla govoriti o postojanju volumena, pokazuje sljedeći primjer.
Primjer 2.2
Neka je
![$ f:[0,1]\times[0,1]\rightarrow R$](img1111.gif)
definirana s
Ova funkcija nije integrabilna, i prema tome odgovarajuće ``tijelo'' nema
volumen u smislu Riemanna.
Zaista, uzmemo li proizvoljnu subdiviziju, proizvoljni 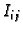 sadrži
i točke s racionalnim koordinatama i one druge. To znači da je uvijek
sadrži
i točke s racionalnim koordinatama i one druge. To znači da je uvijek
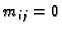 i
i 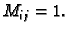 Odatle, za proizvoljnu subdiviziju
Odatle, za proizvoljnu subdiviziju
Tako je
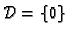
i
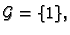
pa je
Dvostruki integral se može koristiti za izračunavanje površine
ravninskog lika. Ako nad likom 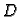 integriramo funkciju
integriramo funkciju 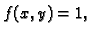 onda time računamo volumen tijela cilindričnog oblika, čija je baza
onda time računamo volumen tijela cilindričnog oblika, čija je baza
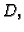 a visina mu je
a visina mu je 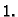 Tako je volumen brojčano jednak površini
baze, tj.
Tako je volumen brojčano jednak površini
baze, tj.
Primjer 2.3
Naći površinu dijela ravnine između kružnica
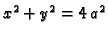
i
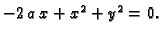
Rješenje. Kanonska jednadžba druge kružnice glasi
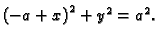
Zbog simetrije, dovoljno je naći površinu iznad osi
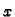
i zatim
pomnožiti s
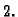
Iz slike se vidi da područje integracije moramo
podijeliti na dva dijela. Tako je
Naravno, ovaj rezultat se lako
može dobiti upotrebom poznate formule za površinu kruga, čija
istinitost, međutim, nigdje dosada nije bila provjerena.
- 1.
- Koji problem rješava dvostruki integral?
- 2.
- Koji uvjet mora ispunjavati funkcija da bi se uopće moglo
postaviti pitanje njezine integrabilnosti?
- 3.
- Kakav treba biti skup po kojem se integrira?
- 4.
- Definirajte dvostruki integral funkcije na
pravokutniku, čije su stranice paralelne koordinatnim osima.
- 5.
- Definirajte sljedeće pojmove: donja Darbouxova suma, gornja
Darbouxova suma, integralna suma.
- 6.
- Zašto se u Darbouxovim sumama pojavljuju
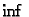 i
i 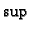 umjesto
umjesto 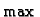 i
i 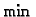 ? U kojem slučaju je to svejedno?
? U kojem slučaju je to svejedno?
- 7.
- Da li je svaka funkcija od dvije varijable integrabilna?
- 8.
- Kako se definira dvostruki integral na proizvoljnom području?
- 9.
- Na koji način se računa dvostruki integral?
- 10.
- Da li se pomoću dvostrukog integrala može računati površina
ravninskog lika?
- 1.
- Naći integral funkcije
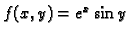 po području
po području
![$ [0,1]\times [0,\pi].$](img1133.gif)
Rješenje.
- 2.
-
Rješenje.
- 3.
-
- 4.
- Zamijeniti poredak integracije u integralu
Rješenje. Područje integracije je
Dakle
- 5.
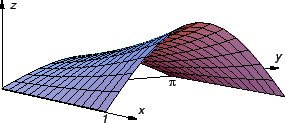
- Naći volumen tijela omeđenog plohama
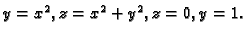
Rješenje. Područje integracije je
Tako je
- 6.
-
- 7.
- Naći volumen tijela iznad područja omeđenog s krivuljama
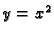 i
i
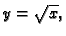 a ispod plohe
a ispod plohe
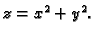
Rješenje. Sjecišta krivulja se dobiju iz jednadžbe
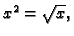 tj.
tj. 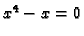 i to su
i to su
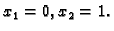 Dakle područje
integracije je
Dakle područje
integracije je




Next: Trostruki integral
Up: Višestruki integrali
Previous: Višestruki integrali
Contents
Index
Salih Suljagic
2000-03-11
![]() Uzmimo najprije jednostavan slučaj neprekidne funkcije
Uzmimo najprije jednostavan slučaj neprekidne funkcije
![]() Neka je pravokutnik
Neka je pravokutnik
![]() u prvom kvadrantu
ravnine
u prvom kvadrantu
ravnine ![]() a ploha neka se nalazi u prvom oktantu. Želimo naći volumen
a ploha neka se nalazi u prvom oktantu. Želimo naći volumen
![]() tijela, koje je odozgo omeđeno plohom
tijela, koje je odozgo omeđeno plohom ![]() a odozdo pravokutnikom
a odozdo pravokutnikom
![]()
![]() segmenta
segmenta ![]() i
i
![]() segmenta
segmenta ![]() Time smo pravokutnik
Time smo pravokutnik
![]() podijelili na podpravokutnike
podijelili na podpravokutnike
![]() Neka je
Neka je ![]() minimalna, a
minimalna, a ![]() maksimalna vrijednost funkcije
maksimalna vrijednost funkcije ![]() na
na
![]() Tada vrijedi
Tada vrijedi
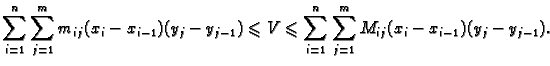
![]() na
na
![]() Podsjetimo se da ograničenost funkcije znači da je slika funkcije
Podsjetimo se da ograničenost funkcije znači da je slika funkcije
![]() ograničen skup u
ograničen skup u ![]()
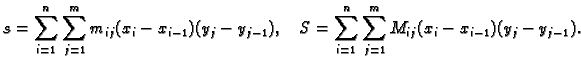
![]() proizvoljan. Broj
proizvoljan. Broj
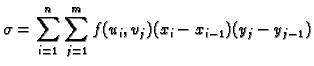
![]() skup svih donjih Darbouxovih suma, a s
skup svih donjih Darbouxovih suma, a s
![]() skup svih gornjih Darbouxovih suma. Neka je
skup svih gornjih Darbouxovih suma. Neka je
![]() Uzmimo novu subdiviziju, koja sadrži sve točke jedne i
druge subdivizije, i neka su
Uzmimo novu subdiviziju, koja sadrži sve točke jedne i
druge subdivizije, i neka su ![]() njezina donja i gornja
Darbouxova suma. Tada vrijedi (slika 2.3)
njezina donja i gornja
Darbouxova suma. Tada vrijedi (slika 2.3)
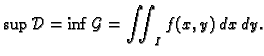
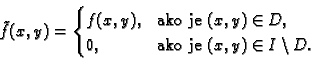

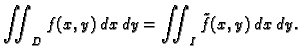
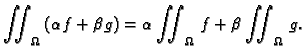
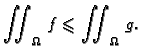
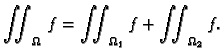
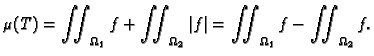
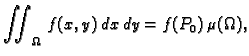
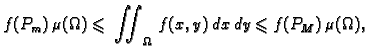
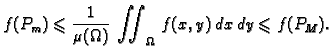
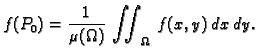
![]() integrabilna na
integrabilna na
![]() Tada za
proizvoljni
Tada za
proizvoljni
![]() postoji takva subdivizija, da je
postoji takva subdivizija, da je
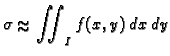
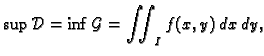
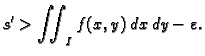
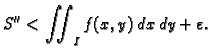
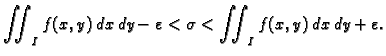
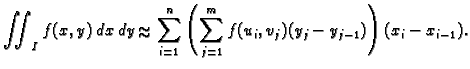
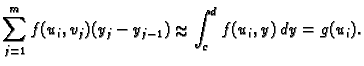
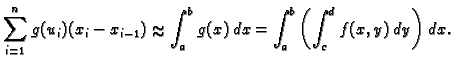
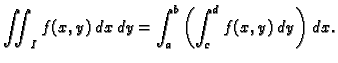
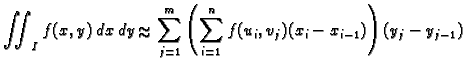
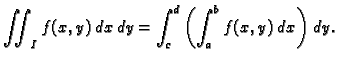
![]() onda se dvostruki integral svodi na
produkt dva jednostruka integrala
onda se dvostruki integral svodi na
produkt dva jednostruka integrala
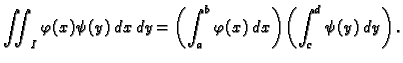
![]() i neka je
i neka je
![]() minimalni
pravokutnik koji sadrži
minimalni
pravokutnik koji sadrži ![]() Neka je dalje područje
Neka je dalje područje ![]() takvo da
se njegov rub sastoji od dvije krivulje, koje su grafovi funkcija od
takvo da
se njegov rub sastoji od dvije krivulje, koje su grafovi funkcija od ![]() i to donji rub neka je graf funkcije
i to donji rub neka je graf funkcije ![]() a gornji graf funkcije
a gornji graf funkcije
![]()
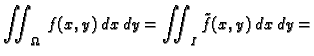
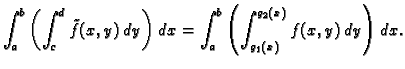
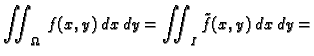
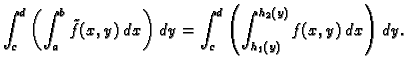
![]() i neka je njegov rub dan plohama koje su
grafovi funkcija
i neka je njegov rub dan plohama koje su
grafovi funkcija ![]() i
i ![]() Neka je ploha
Neka je ploha ![]() gornji, a ploha
gornji, a ploha
![]() donji rub tijela. Neka su funkcije
donji rub tijela. Neka su funkcije ![]() i
i ![]() integrabilne.
Tada je formulom
integrabilne.
Tada je formulom
![$\displaystyle \mu(T)=\iint_{\Omega}\,[f(x,y)-g(x,y)]\,dx\,dy$](img1093.gif)
![$\displaystyle V=\iint_{D} [2-x^2-(x^2+y^2)]\,dx\,dy=
\int_{-1}^1\left(
\int_{-\sqrt{2-2\,x^2}}^{\sqrt{2-2\,x^2}} [2-x^2-
(x^2+y^2)]\,dy \right)\,dx$](img1104.gif)
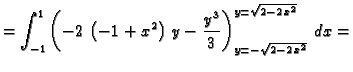
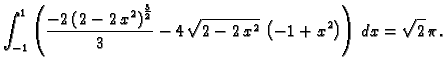
![]() ograničena funkcija na pravokutniku
ograničena funkcija na pravokutniku
![]() i neka je
i neka je
![]() Njezin graf, pravokutnik
Njezin graf, pravokutnik
![]() i ravnine paralelne s osi
i ravnine paralelne s osi ![]() kroz stranice
pravokutnika
kroz stranice
pravokutnika ![]() određuju skup, ``tijelo''
određuju skup, ``tijelo'' ![]() Na temelju do sada
rečenog prirodno je reći da
Na temelju do sada
rečenog prirodno je reći da ![]() ima
volumen, ako je
ima
volumen, ako je ![]() integrabilna na
integrabilna na ![]() i da je u
tom slučaju volumen od
i da je u
tom slučaju volumen od ![]() jednak
jednak
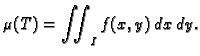

![]() sadrži
i točke s racionalnim koordinatama i one druge. To znači da je uvijek
sadrži
i točke s racionalnim koordinatama i one druge. To znači da je uvijek
![]() i
i ![]() Odatle, za proizvoljnu subdiviziju
Odatle, za proizvoljnu subdiviziju
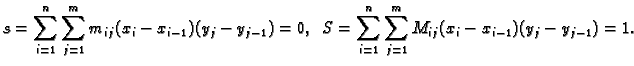
![]() integriramo funkciju
integriramo funkciju ![]() onda time računamo volumen tijela cilindričnog oblika, čija je baza
onda time računamo volumen tijela cilindričnog oblika, čija je baza
![]() a visina mu je
a visina mu je ![]() Tako je volumen brojčano jednak površini
baze, tj.
Tako je volumen brojčano jednak površini
baze, tj.
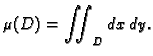
![]()
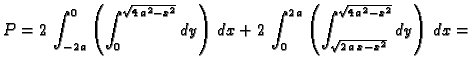
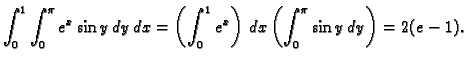
![$\displaystyle I=\int\int_{[1,2]\times[1,2]} \ln xy\,dx\,dy=
\int_1^2 \left(\int_1^2 \ln xy\,dy\right)\,dx=?$](img1136.gif)
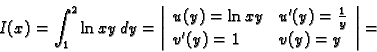
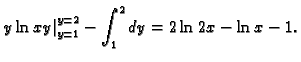
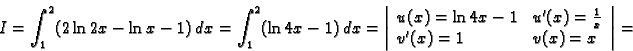
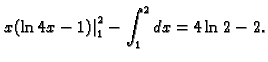
![$\displaystyle I=\int\int_{[0,a]\times[0,a]} e^{-(x^2+y^2)}\,dx\,dy=
\int_0^a \left(\int_0^a e^{-x^2}e^{-y^2}\,dy\right)\,dx=$](img1141.gif)
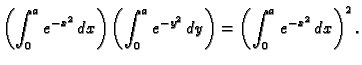
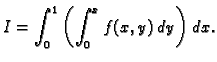
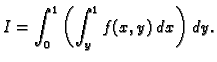
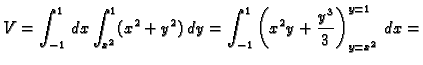
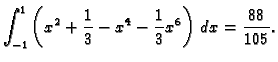
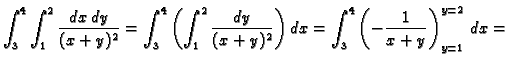
![$\displaystyle \int_3^4\left(\frac{1}{x+1}-\frac{1}{x+2}\right)\,dx=
\left[\ln\vert x+1\vert-\ln\vert x+2\vert\right]_{x=3}^{x=4}=\ln \frac{25}{24}.$](img1153.gif)

![]() tj.
tj. ![]() i to su
i to su
![]() Dakle područje
integracije je
Dakle područje
integracije je