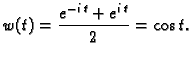Skup7.1
Broj
Neka je
![]()
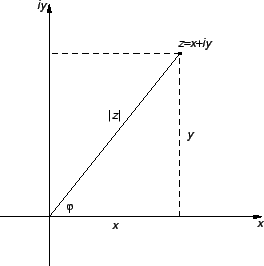
Modul kompleksnog broja je realan broj
Svaki kompleksni broj je potpuno zadan s dva realna broja, i pri tom
je važno koji je prvi (realni dio) a koji drugi (imaginarni dio).
Obratno, svakom uređenom paru realnih brojeva ![]() možemo
pridružiti kompleksni broj
možemo
pridružiti kompleksni broj ![]() Tako je dano obostrano
jednoznačno pridruživanje između skupova
Tako je dano obostrano
jednoznačno pridruživanje između skupova ![]() i
i ![]() To ipak ne
znači da su to isti skupovi. U
To ipak ne
znači da su to isti skupovi. U ![]() imamo operacije zbrajanja i
množenja tj. znamo računati, a u
imamo operacije zbrajanja i
množenja tj. znamo računati, a u ![]() nemamo nikakve operacije.
Elemente iz
nemamo nikakve operacije.
Elemente iz ![]() možemo crtati kao točke u ravnini. Obostrano
jednoznačno pridruživanje između
možemo crtati kao točke u ravnini. Obostrano
jednoznačno pridruživanje između ![]() i
i ![]() omogućava da se i
kompleksni brojevi crtaju u ravnini kao točke. Razlika između
ravnine u kojoj se crtaju uređeni parovi realnih brojeva i ravnine u
kojoj se crtaju kompleksni brojevi je u tome što u ovoj potonjoj
točke možemo zbrajati i množiti, pa zato ova druga ima posebno ime.
Ona se zove
Gaussova ravnina ili
kompleksna ravnina.
omogućava da se i
kompleksni brojevi crtaju u ravnini kao točke. Razlika između
ravnine u kojoj se crtaju uređeni parovi realnih brojeva i ravnine u
kojoj se crtaju kompleksni brojevi je u tome što u ovoj potonjoj
točke možemo zbrajati i množiti, pa zato ova druga ima posebno ime.
Ona se zove
Gaussova ravnina ili
kompleksna ravnina.
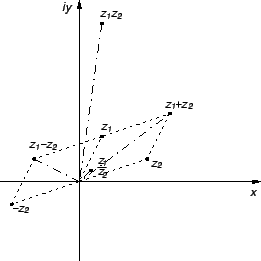
Zbrajanje i odbijanje točaka u Gaussovoj ravnini se vrši po pravilu paralelograma kao na slici.
Neka je
![]() Zapis
Zapis
Neka su
![]() dva kompleksna broja.
dva kompleksna broja.
Otvoren povezan skup u kompleksnoj (Gaussovoj) ravnini zovemo područjem.
Neka je ![]() područje i neka je zadana funkcija
područje i neka je zadana funkcija
![]() Kompleksni broj
Kompleksni broj ![]() možemo napisati u obliku
možemo napisati u obliku
Tako zapravo možemo pisati
Problem crtanja grafa funkcije kompleksne varijable se sastoji u tome
što se uređeni par ![]() kompleksnih brojeva može
identificirati s uređenom četvorkom realnih brojeva
kompleksnih brojeva može
identificirati s uređenom četvorkom realnih brojeva
![]() Uređenu četvorku realnih brojeva nije moguće
nacrtati u ravnini, pa zato funkcije kompleksne varijable prikazujemo
u dvije kompleksne ravnine, i to u
Uređenu četvorku realnih brojeva nije moguće
nacrtati u ravnini, pa zato funkcije kompleksne varijable prikazujemo
u dvije kompleksne ravnine, i to u ![]() -ravnini prikazujemo elemente
domene funkcije, a u
-ravnini prikazujemo elemente
domene funkcije, a u ![]() -ravnini prikazujemo slike funkcije.
-ravnini prikazujemo slike funkcije.
Neka je
![]() Tada je
Tada je
|
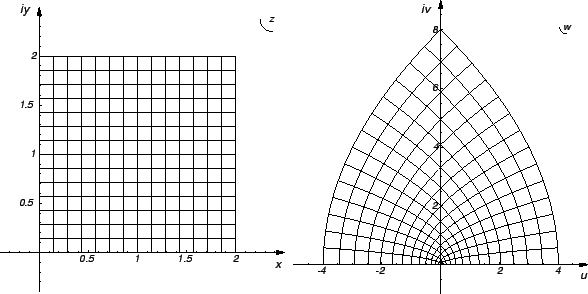
Potpuniju informaciju o tome kako ![]() preslikava točke iz
preslikava točke iz ![]() -ravnine
u točke iz
-ravnine
u točke iz ![]() -ravnine dobivamo, ako uočimo u što se preslikavaju
koordinatne linije u
-ravnine dobivamo, ako uočimo u što se preslikavaju
koordinatne linije u ![]() -ravnini. Tako za
-ravnini. Tako za ![]() iz primjera 7.1
imamo
iz primjera 7.1
imamo
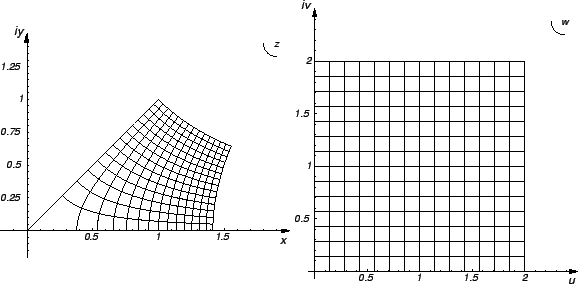
Ako nas, naprotiv, interesira koje to krivulje u ![]() -ravnini prelaze u koordinatne linije u
-ravnini prelaze u koordinatne linije u ![]() -ravnini, onda treba staviti
-ravnini, onda treba staviti
S druge strane
Rješenje. Jedno rješenje je očito ![]() Da nađemo ostala
rješenja, pomnožimo jednadžbu sa
Da nađemo ostala
rješenja, pomnožimo jednadžbu sa ![]() imamo
imamo
![]() tj.
tj.
Zadatak se mogao riješiti i tako da se uvrsti
![]() i izjednače realni i imaginarni dijelovi u jednadžbi. Time bi se
dobio sustav od dvije jednadžbe s dvije nepoznanice
i izjednače realni i imaginarni dijelovi u jednadžbi. Time bi se
dobio sustav od dvije jednadžbe s dvije nepoznanice ![]()
(a)
 |
(b)
 |
Rješenje. Budući da je
![]() trebamo izračunati
trebamo izračunati
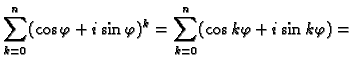
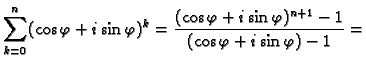
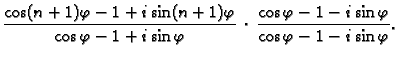
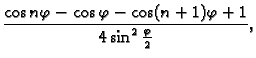
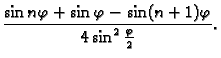
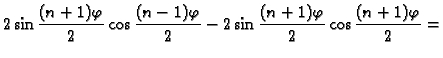
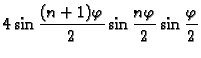
Rješenje. Zadana krivulja ![]() je jedinična kružnica sa središtem u
ishodištu. Kad u
je jedinična kružnica sa središtem u
ishodištu. Kad u ![]() uvrstimo dani
uvrstimo dani ![]() dobivamo
dobivamo