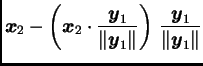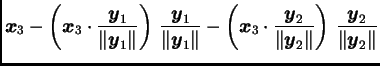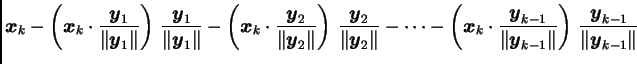Next: Hamilton-Cayleyev teorem za simetrične
Up: Dijagonalizacija simetrične matrice
Previous: Dijagonalizacija simetrične matrice. Različite
Sadržaj
Indeks
Dijagonalizacija simetrične matrice. Opći slučaj.
U općem slučaju se može dogoditi da neke vlastite vrijednosti budu
višestruke. Razmotrimo sljedeći primjer.
Primjer 1.25
Naći vlastite vrijednosti i vlastite vektore matrice
Rješenje. Vlastite vrijednosti su
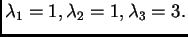
Za
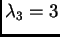 imamo vlastiti vektor
imamo vlastiti vektor
tj. vlastitih vektora ima beskonačno mnogo ali
su svi međusobno kolinearni.
Za
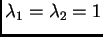 imamo (iz (1.5))
imamo (iz (1.5))
Odavde
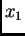
je proizvoljan, i
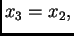
pa je vlastiti vektor
![% latex2html id marker 32282
$\displaystyle \left[\begin{array}{c} x_1 \\ x_2 \...
...{array}\right]+\,x_2\, \left[\begin{array}{c} 0 \\ 1 \\ 1 \end{array}\right],$](img687.png) |
(1.6) |
tj. vlastitih vektora ima beskonačno mnogo
ali sada su oni linearne kombinacije od dva linearno nezavisna
vektora. Kako imamo slobodu izbora, možemo izabrati bilo koja dva
međusobno okomita vektora, tako da i u slučaju višestrukih
vlastitih vrijednosti imamo međusobno okomite vlastite vektore.
Formula (1.6) se može shvatiti kao parametarske
jednadžbe ravnine u prostoru, koja prolazi ishodištem i razapeta je
vektorima
Dakle svaki radijvektor u toj ravnini je vlastiti, s vlastitom
vrijednošću
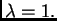
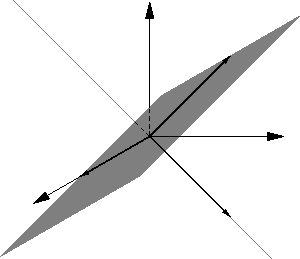
Na slici 1.17 je šatirana ravnina u kojoj je svaki vektor
vlastiti s vlastitom vrijednošću 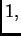 i također je povučen pravac
na kojem je svaki vektor vlastiti s vlastitom vrijednošću
i također je povučen pravac
na kojem je svaki vektor vlastiti s vlastitom vrijednošću 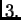
Slika 1.17:
Vlastiti vektori i njihove slike (višestruke vlastite vrijednosti).
|
|
Općenito se događa sljedeće. 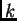 -struka vlastita vrijednost
simetrične matrice vodi na sustav jednadžbi koji ima beskonačno
mnogo rješenja određenih pomoću
-struka vlastita vrijednost
simetrične matrice vodi na sustav jednadžbi koji ima beskonačno
mnogo rješenja određenih pomoću 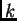 parametara. Izborom ovih
parametara tako da jedan bude
parametara. Izborom ovih
parametara tako da jedan bude 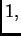 a ostali
a ostali 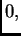 dobivamo
dobivamo 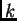 linearno
nezavisnih vektora. Ako tako napravimo za svaku višestruku vlastitu
vrijednost, i dodamo vlastite vektore koji pripadaju jednostrukim
vlastitim vrijednostima, dobit ćemo
linearno
nezavisnih vektora. Ako tako napravimo za svaku višestruku vlastitu
vrijednost, i dodamo vlastite vektore koji pripadaju jednostrukim
vlastitim vrijednostima, dobit ćemo 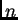 linearno nezavisnih vlastitih
vektora simetrične matrice
linearno nezavisnih vlastitih
vektora simetrične matrice 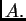 Od njih kao stupaca formiramo matricu
Od njih kao stupaca formiramo matricu
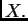 Ona je regularna, i vrijedi
Ona je regularna, i vrijedi
Pomnožimo s lijeva matricom 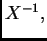 i
dobit ćemo, kao i prije
i
dobit ćemo, kao i prije
Definicija 14
Neka je
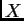
regularna matrica i neka je
Tada
kažemo da su matrice
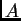
i
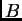 slične
slične.
Ako među matricama sličnim matrici 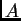 postoji dijagonalna, onda
kažemo da se matrica
postoji dijagonalna, onda
kažemo da se matrica 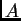 može dijagonalizirati.
Dijagonalizacija
matrice je postupak nalaženja one regularne matrice
može dijagonalizirati.
Dijagonalizacija
matrice je postupak nalaženja one regularne matrice 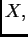 koja ima
svojstvo da je
koja ima
svojstvo da je
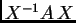 dijagonalna matrica.
dijagonalna matrica.
U skladu s ovom definicijom, možemo zaključiti da se proizvoljna
simetrična matrica 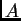 može dijagonalizirati. U slučaju kad su
vlastite vrijednosti međusobno različite, dijagonalizacija se vrši
pomoću matrice čiji su stupci međusobno okomiti vlastiti
vektori matrice
može dijagonalizirati. U slučaju kad su
vlastite vrijednosti međusobno različite, dijagonalizacija se vrši
pomoću matrice čiji su stupci međusobno okomiti vlastiti
vektori matrice 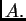
No, i u slučaju višestrukih vlastitih vrijednosti matrica 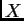 se
može izabrati tako da su joj stupci međusobno okomiti. Doista, ako
su
se
može izabrati tako da su joj stupci međusobno okomiti. Doista, ako
su
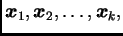 linearno nezavisni vlastiti vektori, onda su vektori
linearno nezavisni vlastiti vektori, onda su vektori
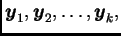 dobiveni po formulama
dobiveni po formulama
međusobno okomiti, i svaki od njih je vlastiti pripadajući istoj
vlastitoj vrijednosti. Ovaj postupak se zove Gram-Schmidtov
postupak ortogonalizacije.
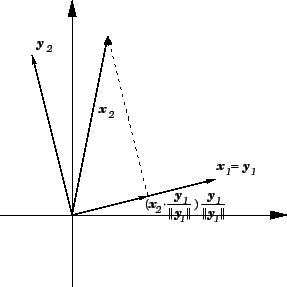
Ideja Gram-Schmidtovog postupka ortogonalizacije je jednostavna i
prirodna. Prvi vektor ostavimo na miru. Njime je određen
pravac. Drugi vektor projiciramo ortogonalno na taj pravac, i zatim
tu projekciju odbijemo od drugog vektora. Time naravno dobivamo vektor
koji je okomit na vektor na koji smo projicirali (sl. 1.18). S tako dobivenim
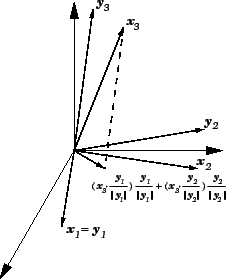
vektorima razapnemo ravninu. Treći vektor
projiciramo ortogonalno na tu ravninu, i odbijemo projekciju od njega.
Time smo dobili vektor okomit na ravninu (sl. 1.19), itd.
Slika 1.18:
Gram-Schmidtov postupak ortogonalizacije u ravnini.
|
|
Slika 1.19:
Gram-Schmidtov postupak ortogonalizacije u prostoru.
|
|
Ako međusobno okomite vlastite vektore normiramo (podijelimo s
njihovom duljinom), onda matrica
![$ X=[x_{ij}],$](img710.png) čiji su stupci vektori
čiji su stupci vektori
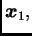
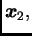
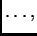
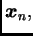 postaje ortogonalna. U tom slučaju je
postaje ortogonalna. U tom slučaju je
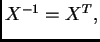 pa je
pa je





Next: Hamilton-Cayleyev teorem za simetrične
Up: Dijagonalizacija simetrične matrice
Previous: Dijagonalizacija simetrične matrice. Različite
Sadržaj
Indeks
2001-10-26
![% latex2html id marker 32252
$\displaystyle A=\left[
\begin{array}{ccc}
1 & 0 & 0 \\
0 & 2 & -1 \\
0 & -1 & 2
\end{array} \right].$](img679.png)
![]()
![]() imamo vlastiti vektor
imamo vlastiti vektor
![% latex2html id marker 32258
$\displaystyle \left[\begin{array}{c}
0 \\ x_2 \\...
...nd{array}\right]=x_2\left[\begin{array}{c}
0 \\ 1 \\ -1
\end{array}\right],$](img682.png)
![]() imamo (iz (1.5))
imamo (iz (1.5))
![% latex2html id marker 32284
$\displaystyle \left[\begin{array}{c}
1 \\ 0 \\ ...
...], \quad \quad \quad \left[\begin{array}{c}
0 \\ 1 \\ 1
\end{array}\right].$](img688.png)
![]() i također je povučen pravac
na kojem je svaki vektor vlastiti s vlastitom vrijednošću
i također je povučen pravac
na kojem je svaki vektor vlastiti s vlastitom vrijednošću ![]()
![% latex2html id marker 32282
$\displaystyle \left[\begin{array}{c} x_1 \\ x_2 \...
...{array}\right]+\,x_2\, \left[\begin{array}{c} 0 \\ 1 \\ 1 \end{array}\right],$](img687.png)