Dijagonalizacija matrice sustava

Sustav

$$\boldsymbol{y}'(x)=A\,\boldsymbol{y}(x)+\boldsymbol{f}(x)$$

možemo vrlo elegantno riješiti, ako se matrica $A$ može dijagonalizirati. Pretpostavimo da je to moguće, i da je

$$X^{-1}A\,X=[\lambda_j\,\delta_{ij}].$$

Da bismo dobili dijagonalnu matricu pomnožimo jednadžbu s $X^{-1}$ s lijeva.

$$X^{-1}\,\boldsymbol{y}'(x) = X^{-1}A\,\boldsymbol{y}(x) + X^{-1}\,\boldsymbol{f}(x),$$

$$X^{-1}\,\boldsymbol{y}'(x)=X^{-1}A\,X\,X^{-1}\,\boldsymbol{y}(x) + X^{-1}\,\boldsymbol{f}(x),$$

$$X^{-1}\,\boldsymbol{y}'(x)=[\lambda_j\,\delta_{ij}]\,X^{-1}\,\boldsymbol{y}(x) + X^{-1}\,\boldsymbol{f}(x),$$

$$\boldsymbol{z}'(x)=[\lambda_j\,\delta_{ij}]\,\boldsymbol{z}(x) + \boldsymbol{g}(x),$$

gdje smo stavili

$$\boldsymbol{z}(x)=X^{-1}\,\boldsymbol{y}(x),\qquad \boldsymbol{g}(x)=X^{-1}\,\boldsymbol{f}(x)$$

Ovaj sustav, kad se raspiše, svodi se na $n$ nezavisnih jednadžbi

$$z_i '(x)=\lambda_i\,z_i (x) + g_i(x),\hspace{1cm}i=1,2,\ldots, n.$$

Svaka od ovih jednadžbi je linearna diferencijalna jednadžba 1. reda, čije rješenje je

$$z_i(x)=e^{\lambda_i\,x}\left(C_i + \int g_i(x)\,e^{-\lambda_i\,x}\,dx\right),\hspace{1cm}i=1,2,\ldots, n.$$

Opće rješenje početnog sustava dobijemo tako da nađemo $\boldsymbol{y}(x)$ po formuli

$$\boldsymbol{y}(x) = X\,\boldsymbol{z}(x).$$

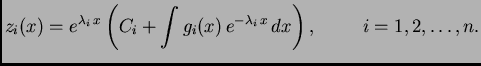
Kada je dan Cauchyjev problem

$$\boldsymbol{y}'(x) = A\,\boldsymbol{y}(x) + \boldsymbol{f}(x),\quad \boldsymbol{y}(x_0)=\boldsymbol{y}_0,$$

rješenje dobijemo određujući konstante $C_i$ iz početnog uvjeta

$$\boldsymbol{y}(x_0)=\boldsymbol{y}_0.$$

Ova metoda omogućava elegantno rješavanje, ako je matrica simetrična. Neke nesimetrične matrice se također mogu dijagonalizirati, kao što pokazuje primjer 1.24. Riješimo sada metodom dijagonalizacije upravo jedan takav primjer sustava diferencijalnih jednadžbi.

Primjer 1.34   Riješimo sljedeći sustav linearnih diferencijalnih jednadžbi 1. reda s konstantnim koeficijentima metodom dijagonalizacije.

$$y'_1 = 3\,y_1-2\,y_2-4\,y_3 + x\,\sin x$$

$$y'_2 = -y_1+y_2+y_3 + \cos 2\,x$$

$$y'_3 = y_1-2\,y_2-2\,y_3 + x^2-1.$$

Rješenje. Matrica sustava je

$$A=\left[ \begin{array}{ccc} 3 & -2 & -4 \\ -1 & 1 & 1 \\ 1 & -2 & -2 \end{array} \right].$$

U primjeru 1.24 smo ustanovili da su vlastite vrijednosti $\lambda_1=1,\lambda_2=-1,\lambda_3=2.$ Vlastiti vektori su

$$\left[\begin{array}{c} 1 \\ -1 \\ ... ...ray}\right],\quad \left[\begin{array}{c} -2 \\ 1 \\ -1 \end{array}\right].$$

Tako imamo

$$X = \left[\begin{array}{ccc} 1 & 1 ... ... \left[\begin{array}{c} x\,\sin x \\ \cos 2\,x \\ x^2-1 \end{array}\right].$$

Zatim

$$X^{-1}\,A\,X = \left[\begin{array}{c... ...\,\sin x \\ -1 + x^2 + \cos 2\,x \\ -1 + x^2 - x\,\sin x \end{array}\right].$$

Tako se sustav raspada na tri nezavisne linearne diferencijalne jednadžbe 1. reda.

$$z'_1 = z_1 -1 + x^2 - \cos 2\,x - x\,\sin x$$

$$z'_2 = -z_2 -1 + x^2 + \cos 2\,x$$

$$z'_3 = 2\,z_3 -1 + x^2 - x\,\sin x.$$

Svaku od njih riješimo, na pr. po formuli za rješenje linearne diferencijalne jednadžbe 1. reda. Rješenje je

$${z_1(x)} = {-1 - 2\,x - x^2 + C_1\,e^x + \frac{1}{2}\,\cos x + \frac{1}{2}\,x\,\cos x + \frac{1}{5}\,\cos 2\,x + \frac{1}{2}\,x\,\sin x}$$

$${- \frac{2}{5}\,\sin 2\,x,}$$

$${z_2(x)} = {1 - 2\,x + x^2 + C_2\,e^{-x} + \frac{1}{5}\,\cos 2\,x + \frac{2}{5}\,\sin 2\,x,}$$

$${z_3(x)} = { \frac{1}{4} - \frac{1}{2}\,x - \frac{1}{2}\,x^2 + C_3\,e^{2\,x} + \frac{4}{25}\,\cos x + \frac{1}{5}\,x\,\cos x + \frac{3}{25}\,\sin x +}$$

$${+ \frac{2}{5}\,x\,\sin x.}$$

Da dobijemo rješenje zadanog sustava, trebamo naći $\boldsymbol{y}(x)=X\,\boldsymbol{z}(x).$ To znači

$$y_1 = z_1 + z_2 - 2\,z_3$$

$$y_2 = -z_1 + z_3$$

$$y_3 = z_1 + z_2 - z_3$$

tj.

$$y_1(x) = -{\frac{1}{2}} - 3\,x + x^2 + C_1\,e^x + {C_2\,e^{-x}} - 2\,C_3\,{e^{2\,x}} + {\frac{1}{50}\,\left( 9 + 5\,x \right) \,\cos x} +$$

$$+ {\frac{2}{5}\,\cos 2\,x} - {\frac{6}{25}\,\sin x} - {\frac{3}{10}\,x\,\sin x},$$

$$y_2(x) = \frac{5}{4} + \frac{3}{2}\,x + \frac{1}{2}\,x^2 - C_1\,e^x + C_3\... ...} - \frac{1}{50}\,\left( 17 + 15\,x \right) \,\cos x - \frac{1}{5}\,\cos 2\,x +$$

$$+\frac{3}{25}\,\sin x - \frac{1}{10}\,x\,\sin x + \frac{2}{5}\,\sin 2\,x,$$

$$y_3(x) = -{\frac{1}{4}} - {\frac{7}{2}\,x} + {\frac{1}{2}\,x^2} + C_1\,e^x... ...{-x}} - C_3\,{e^{2\,x}} + {\frac{1}{50}\,\left( 17 + 15\,x \right) \, \cos x} +$$

$$+{\frac{2}{5}\,\cos 2\,x} - {\frac{3}{25}\,\sin x} + {\frac{1}{10}\,x\,\sin x}.$$

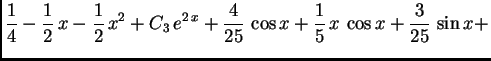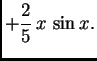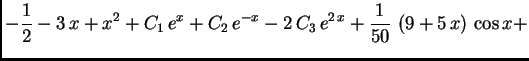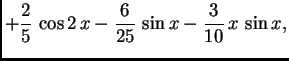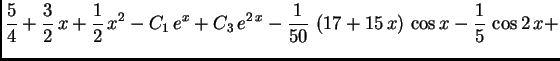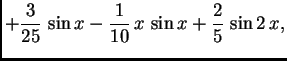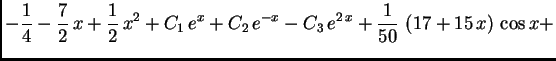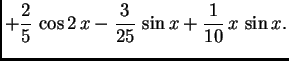Na slici 1.29 su dani grafovi rješenja uz zadani početni uvjet

$$y_1(0) = -1,\qquad y_2(0) = 1,\qquad y_3(0) = 0,$$

koje je

$$y_1(x) = -\frac{1}{2} - \frac{1}{5}\,e^{-x} + \frac{3}{10}\,{e^x} - \frac{59}{50}\,e^{2\,x} - 3\,x + x^2 + \frac{1}{50}\left( 9 + 5\,x \right) \,\cos x +$$

$$+\frac{2}{5}\,\cos 2\,x - \frac{6}{25}\,\sin x - \frac{3}{10}\,x\,\sin x,$$

$$y_2(x) = \frac{5}{4} - \frac{3}{10}\,{e^x} + \frac{59}{100}\,e^{2\,x} + \f... ...}{2}\,x + \frac{1}{2}\,x^2 - \frac{1}{50}\,\left( 17 + 15\,x \right) \,\cos x -$$

$$-\frac{1}{5}\,\cos 2\,x + \frac{3}{25}\,\sin x - \frac{1}{10}\,x\,\sin x + \frac{2}{5}\,\sin 2\,x,$$

$$y_3(x) = -\frac{1}{4} - \frac{1}{5}\,e^{-x} + \frac{3}{10}\,e^x - \frac{59... ...7}{2}\,x + \frac{1}{2}\,{x^2} + \frac{1}{50}\left(17 + 15\,x \right) \,\cos x +$$

$$+\frac{2}{5}\,\cos 2\,x - \frac{3}{25}\,\sin x + \frac{1}{10}\,x\,\sin x.$$

Slika 1.29: Rješenje sustava uz navedeni početni uvjet.

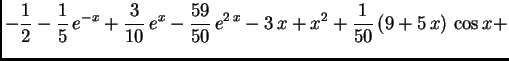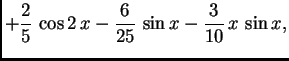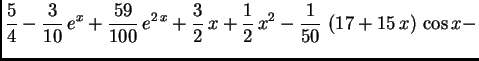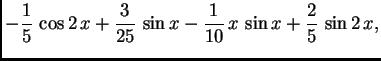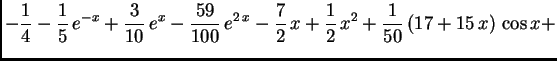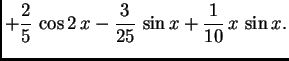No postoje matrice koje se ne mogu dijagonalizirati. Najjednostavniji oblik na koji se proizvoljna matrica može svesti je Jordanova forma. U slučaju međusobno različitih vlastitih vrijednosti Jordanova forma je dijagonalna matrica s vlastitim vrijednostima na glavnoj dijagonali, dok u slučaju višestrukih vlastitih vrijednosti, na pr. trostruke vlastite vrijednosti $\lambda,$ Jordanova forma matrice trećeg reda je jedna od sljedeće tri matrice

$$\left[\begin{array}{ccc} \lambda & ... ... \lambda & 1 & 0 \\ 0 & \lambda & 1 \\ 0 & 0 & \lambda \end{array}\right].$$

Detaljnije o Jordanovoj formi u [4].