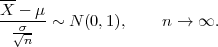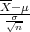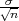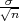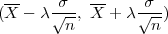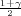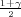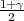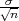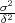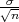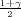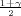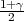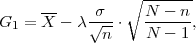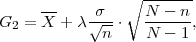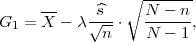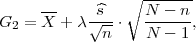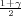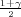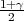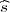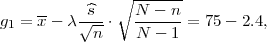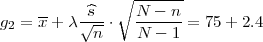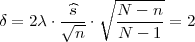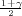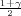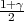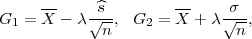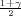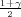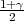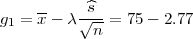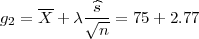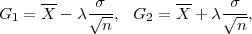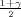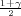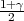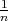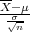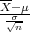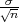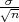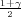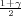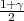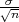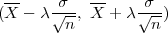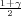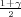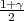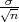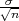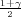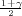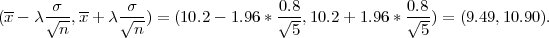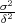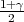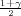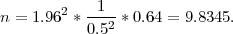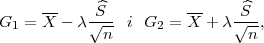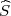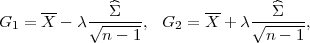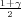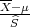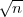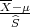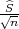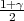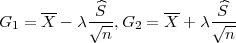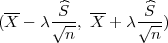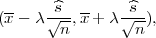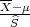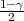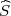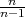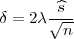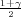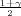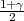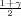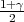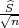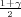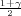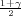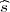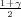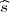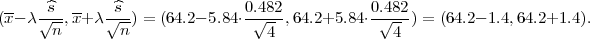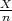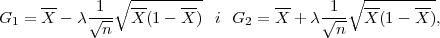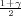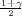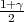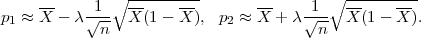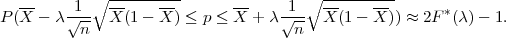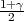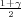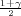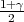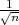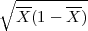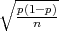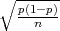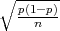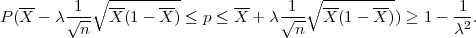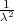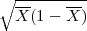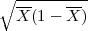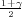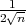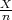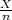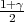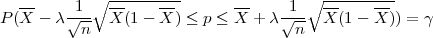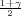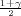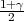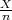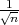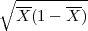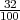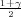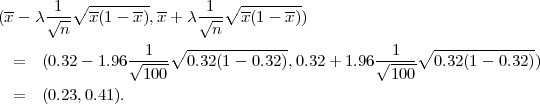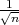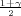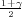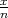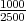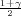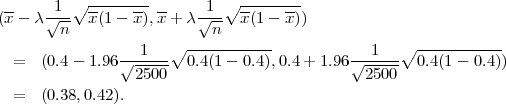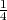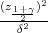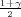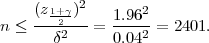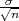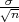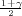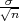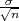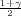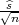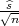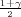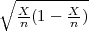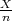Poglavlje 13
INTERVAL POVJERENJA ZA OČEKIVANJE
Definicija 13.1 (KVANTIL)
Neka je X slučajna varijabla s funkcijom distribucije F(x)i neka je zadan
q ∈ (0,1). Broj zq zove se kvantil distribucije F ako vrijedi F(zq) = q.
Definicija 13.2 (INTERVAL POVJERENJA POUZDANOSTI γ)
Neka je (X1,X2,..Xn) slučajni uzorak slučajne varijable X koja ima poznatu
distribuciju s nepoznatim parametrom t i neka je zadana pouzdanost γ ∈ (0,1).
Za procjenitelje G1 = h1(X1,X2,..Xn) i G2 = h2(X1,X2,..Xn) za parametar t
kažemo da čine interval povjerenja (G1,G2) za parametar t s pouzdanošću γ ako
vrijedi: P(G1 < t < G2) ≥ γ.
Parametar t poprimit će vrijednosti unutar intervala (g1,g2) s puzdanošću γ, gdje
je g1 = h1(x1,x2,..xn), g2 = h2(x1,x2,..xn).
13.1 INTERVAL POVJERENJA ZA OČEKIVANJE
ako je veliki uzorak n →∞
MOTIV 13.1
Slučajni uzorak od 50 studenata za broj bodova (max 100 bodova) iz VIS-a od
ukupno 200 studenata ove generacije pokazuje uzoraču aritmetičku sredinu 75 i
korigiranu uzoračku standardnu devijaciju 10.
(a) Odredite interval povjerenja za očekivani broj bodova iz VIS-a za ovu genaraciju
studenata s pouzdanošću 95%.
(b) Kolika je pouzdanost da će interval povjerenja za očekivani broj bodova biti
[74,76]?
(c) Odredite interval povjerenja za očekivani broj bodova iz VIS-a s pouzdanošću
95% ako je ovo bio uzorak iz podataka za sve generacije studenata koje je nastavnik
vodio.
Dokaz: tko želi znati više
Prema Centralnom graničnom teormu za aritmetčku sredinu
Primijenimo CGT na simetrični interval (-λ,λ) :
P(-λ < 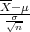 < λ) ≈ F*(λ) - F*(-λ) = 2F*(λ) - 1
< λ) ≈ F*(λ) - F*(-λ) = 2F*(λ) - 1
tj.
P(X - λ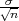 < μ < X + λ
< μ < X + λ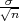 ) ≈ 2F*(λ) - 1.
) ≈ 2F*(λ) - 1.
Ako je zadana pozdanost γ, P(G1 < μ < G2) = γ, onda možemo odrediti λ tako da
vrijedi F*(λ) = 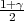 tj. λ = z
tj. λ = z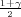 kvantil standardne normalne distribucije
F*(z
kvantil standardne normalne distribucije
F*(z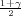 ) =
) = 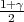 .
.
Zaključujemmo da je za velike n P(X - λ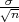 < μ < X + λ
< μ < X + λ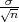 ) = γ.
) = γ.
Procjenitelji G1 = X - λ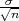 , G2 = X + λ
, G2 = X + λ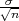 čine interval povjerenja
čine interval povjerenja
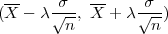
za parametar očekivanja μ slučajne varijable X s puzdanošću γ ako je poznata
varijanca σ2.
Parametar očekivanja μ s pozdanošću γ poprimit će vrijednosti u u intervalu
(x - λ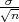 ,x + λ
,x + λ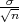 ), gdje je λ = z
), gdje je λ = z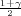 kvantil standardne normalne distribucije
F*(z
kvantil standardne normalne distribucije
F*(z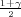 ) =
) = 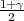 .
.
NAPOMENA 13.2 (uzorak bez vračanja u konačnoj populaciji)
Neka je (X1,X2,..Xn) slučajni uzorak slučajne varijable X koja ima poznatu
distribuciju s nepoznatim parametrom očekivanje μ i poznatom varijancom σ2 (ili
poznatom korigiranom uzoračkom varijancom 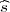 2).
2).
Neka je uzet uzorak bez vraćanja iz konačne populacije veličine N. Ako je veliki
uzorak (n → ∞), ( n ≤ 30) onda interval povjerenja (G1,G2) za parametar
očekivanja μ s puzdanošću γ čine procjenitelji
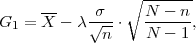
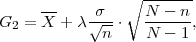
ili
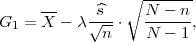
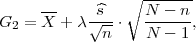
gdje je X uzoračka aritmetička sredina, a λ = z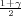 kvantil standardne normalne
distribucije F*(z
kvantil standardne normalne
distribucije F*(z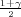 ) =
) = 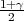 .
.
PRIMJER 13.1 motiv
Slučajni uzorak od 50 studenata za broj bodova (max 100 bodova) iz VIS-a od
ukupno 200 studenata ove generacije pokazuje uzoraču aritmetičku sredinu 75 i
korigiranu uzoračku standardnu devijaciju 10.
(a) Odredite interval povjerenja za očekivani broj bodova iz VIS-a za ovu genaraciju
studenata s pouzdanošću 95%.
(b) Kolika je pouzdanost da će interval povjerenja za očekivani broj bodova biti
[74,76]?
(c) Odredite interval povjerenja za očekivani broj bodova iz VIS-a s pouzdanošću
95% ako je ovo bio uzorak iz podataka za sve generacije studenata koje je nastavnik
vodio.
Rješenje: Pretpostavljamo da je X slučajna varijabla (statističko obilježe) broj bodova na
ispitu iz VIS-a.
Prema prethodnoj napomeni odredit ćemo interval povjerenja za očekivanje ako je
veličina uzorka velika n > 30 za konačnu populaciju N = 200 pri uzorku bez
vraćanja.
Iz zadatka išćitavamo podatke: 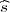 = 10, N = 200, n = 50, x = 75.
= 10, N = 200, n = 50, x = 75.
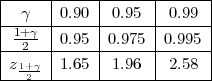
(a) Za pouzdanost γ = 0.95 koeficijent λ = 1.96.
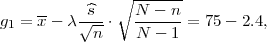
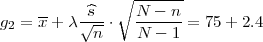
Uz pouzdanost 95% broj bodova za kolegij VIS za studente ove generacije je unutar
intervala [75 - 2.4,75 + 2.4].
(b) Ako je širina intervala δ = 2 onda je
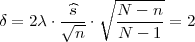 pa
je 2λ ⋅ 1.23 = 2 Dobili smo vrijednost λ = 0.81.
pa
je 2λ ⋅ 1.23 = 2 Dobili smo vrijednost λ = 0.81.
Veza λ i γ dana izrazom λ = z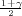 . Kako je kvantil z
. Kako je kvantil z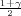 = 0.81 iz tablice za normalnu
razdiobu očitamo da je F(0.81) = 0.791.
= 0.81 iz tablice za normalnu
razdiobu očitamo da je F(0.81) = 0.791.
Pouzdanost γ odredujemo iz izraza 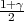 = 0.791
= 0.791
Tražena puzdanost je γ = 0.582.
Uz pouzdanost 58.2% broj bodova za kolegij VIS u populaciji ove generacije je
unutar intervala [75 - 1,75 + 1].
(c) U ovom slučaju imamo veliku populaciju pa je interval povjerenja (G1,G2) za
parametar očekivanja μ s puzdanošću γ
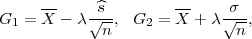
gdje je X uzoračka aritmetička sredina, a λ = z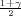 kvantil standardne normalne
distribucije F*(z
kvantil standardne normalne
distribucije F*(z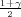 ) =
) = 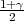 .
.
Za pouzdanost γ = 0.95 koeficijent λ = 1.96.
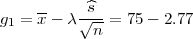
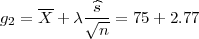
Uz pouzdanost 95% broj bodova za kolegij VIS u cjelokupnoj populaciji je unutar
intervala [75 - 2.77,75 + 2.77].
13.2 INTERVAL POVJERENJA ZA OČEKIVANJE NORMALNE distribucije
ako je varijanca poznata
MOTIV 13.2
Neka slučajna varijabla ima normalnu distribuciju
X ~ N(μ,σ2) nepoznatog očekivanja i poznate varijance σ2 = 0.64. Koliki
minimalni uzorak treba uzeti da bi greška procjene očekivanja μ bila najviše jednaka
0.5, uz pouzdanost γ = 0.95?
Dokaz: tko želi znati više
Neka je X ~ N(μ,σ2), onda je X ~ N(μ,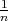 σ2), a
σ2), a 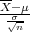 ~ N(0,1).
~ N(0,1).
Na simetričnom intervalu (-λ,λ) :
P(-λ < 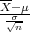 < λ) = F*(λ) - F*(-λ) = 2F*(λ) - 1
< λ) = F*(λ) - F*(-λ) = 2F*(λ) - 1
tj.
P(X - λ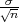 < μ < X + λ
< μ < X + λ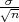 ) = 2F*(λ) - 1.
) = 2F*(λ) - 1.
Ako je zadana pozdanost γ, P(G1 < μ < G2) = γ, onda možemo odrediti λ tako da
vrijedi F*(λ) = 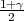 tj. λ = z
tj. λ = z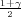 je kvantil standardne normalne distribucije
F*(z
je kvantil standardne normalne distribucije
F*(z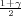 ) =
) = 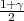 .
.
Procjenitelji G1 = X - λ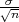 , G2 = X + λ
, G2 = X + λ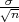 čine interval povjerenja
čine interval povjerenja
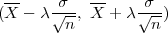
za parametar očekivanja μ slučajne varijable X ~ N(μ,σ2) s pouzdanošću γ ako je
poznata varijanca σ2.
Parametar očekivanja μ s pozdanošću γ poprimit će vrijednosti u u intervalu
(x - λ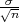 ,x + λ
,x + λ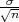 ), gdje je λ = z
), gdje je λ = z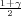 kvantil standardne normalne distribucije
F*(z
kvantil standardne normalne distribucije
F*(z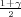 ) =
) = 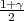 .
.
PRIMJER 13.2 Neka slučajna varijabla ima normalnu distribuciju
X ~ N(μ,σ2 = 0.64). Uzet je uzorak veličine n = 5 i dobivena je vrijednost
uzoračke aritmetičke sredine x = 10.2. Odredite interval povjerenja za očekivanje
slučajne varijable s pouzdanošću γ = 0.95.
Rješenje: P(X - λ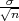 < μ < X + λ
< μ < X + λ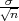 ) = γ.
) = γ.
Za očekivanje μ interval povjerenja pouzdanosti γ je (X-λ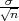 , X + λ
, X + λ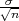 ), gdje je λ =
z
), gdje je λ =
z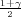 kvantil standardne normalne distribucije.
kvantil standardne normalne distribucije.
Iz tablice očitavamo za γ = 0.95, λ = z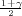 = 1.96.
= 1.96.
Koristeći date vrijednosti iz uzorka n = 5, x = 10.2 dobivamo interval povjerenja za
μ :
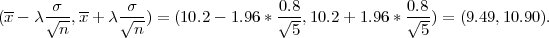
PRIMJER 13.3 motiv
Neka slučajna varijabla ima normalnu distribuciju
X ~ N(μ,σ2) nepoznatog očekivanja i poznate varijance σ2 = 0.64. Koliki
minimalni uzorak treba uzeti da bi greška procjene očekivanja μ bila najviše jednaka
0.5, uz pouzdanost γ = 0.95?
Rješenje: n = 4λ2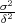 = λ2
= λ2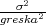 , gdje je λ = z
, gdje je λ = z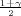 kvantil standardne normalne,
F*(z
kvantil standardne normalne,
F*(z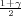 ) =
) = 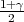 .
.
Iz tablice očitavamo za γ = 0.95, λ = z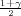 = 1.96.
= 1.96.
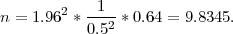
13.3 INTERVAL POVJERENJA ZA OČEKIVANJE NORMALNE distribucije
ako je varijanca nepoznata
MOTIV 13.3 U četiri mjerenja Rockwellove tvrdoće jedne ploče radnici du dobili
sljedeće vrijednosti:
64.9,64.1,63.8,64.0.
Odredite interval povjerenja za očekivanu vrijednost tvrdoće s pouzdanošću 99%.
TEOREM 13.3 Neka je (X1,X2,..Xn) slučajni uzorak slučajne varijable
X ~ N(μ,σ2) s nepoznatim parametrom očekivanje μ i nepoznatom varijancom
σ2.
(i) Interval povjerenja (G1,G2) za parametar očekivanja μ s pouzdanošću γ
čine procjenitelji :
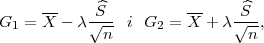
gdje je X uzoračka aritmetička sredina, 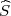 2 korigirana uzoračka varijanca,
2 korigirana uzoračka varijanca,
a λ = z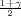 kvantil sudentove distribucije t(n - 1), F(z
kvantil sudentove distribucije t(n - 1), F(z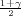 ) =
) = 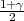 .
.
(ii) Interval povjerenja (G1,G2) za parametar očekivanja μ s pouzdanošću γ
čine procjenitelji:
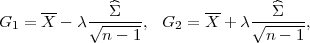
gdje je X uzoračka aritmetička sredina, 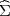 2 uzoračka varijanca, a λ = z
2 uzoračka varijanca, a λ = z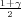
kvantil studentove distribucije t(n - 1).
Dokaz: tko želi znati više
(i) Neka je X ~ N(μ,σ2), onda je Y = 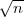
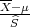 ~ t(n - 1).
~ t(n - 1).
Na simetričnom intervalu (-λ,λ) :
P(-λ ≤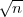
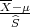 ≤ λ) = F(λ) - F(-λ) = 2F(λ) - 1
≤ λ) = F(λ) - F(-λ) = 2F(λ) - 1
tj.
P(X - λ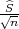 < μ < X + λ
< μ < X + λ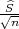 ) = 2F(λ) - 1.
) = 2F(λ) - 1.
Ako je zadana pozdanost γ, P(G1 < μ < G2) = γ, onda možemo odrediti λ tako
da vrijedi F(λ) = 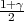 tj. λ = z
tj. λ = z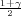 kvantil studentove distribucije t(n - 1),
F(z
kvantil studentove distribucije t(n - 1),
F(z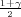 ) =
) = 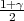 .
.
Procjenitelji
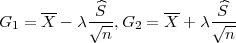 čine
interval povjerenja
čine
interval povjerenja
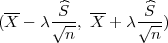
za parametar očekivanja μ slučajne varijable X ~ N(μ,σ2) s puzdanošću γ ako je
nepoznata varijanca σ2.
Parametar očekivanja μ s pozdanošću γ poprimit će vrijednosti u intervalu
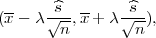 gdje
je λ = z
gdje
je λ = z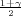 kvantil studentove distribucije
kvantil studentove distribucije
F(z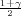 ) =
) = 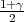 .
.
Ako je tablica studentove distribucije Y ~ t(n - 1,) dana u obliku
P(|Y | > ε) = p, onda λ tražimo tako da je P(|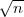
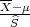 | < λ) =
| < λ) = 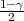 .
.
(ii) Koristimo vezu 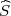 2 =
2 = 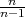
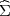 2.
2.
PRIMJER 13.4 Neka slučajna varijabla ima normalnu distribuciju
X ~ N(μ,σ2) nepoznate varijance σ2. Uzet je utorak veličine n = 5 i dobivena je
vrijednost uzoračke aritmetičke sredine x = 10.2, i vrijednost korigirane uzoračke
varijance 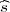 2 = 0.64. Odredite interval povjerenja za očekivanje slučajne varijable
s pouzdanošću γ = 0.95.
2 = 0.64. Odredite interval povjerenja za očekivanje slučajne varijable
s pouzdanošću γ = 0.95.
Rješenje: P(X - λ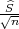 < μ < X + λ
< μ < X + λ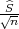 ) = γ.
) = γ.
Za očekivanje μ interval povjerenja pouzdanosti γ je (X-λ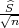 ,X + λ
,X + λ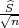 ), gdje je λ =
z
), gdje je λ =
z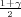 kvantil studentove distribucije t(n - 1).
kvantil studentove distribucije t(n - 1).
Za n=5, λ = z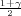 je kvantil studentove distribucije t(4).
je kvantil studentove distribucije t(4).
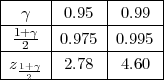
Iz tablice očitavamo za γ = 0.95, λ = z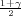 = 2.78.
= 2.78.
Koristeći date vrijednosti iz uzorka x = 10.2, i 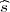 2 = 0.64 dobivamo interval povjerenja
za μ :
2 = 0.64 dobivamo interval povjerenja
za μ :
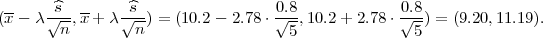
PRIMJER 13.5 motiv
U četiri mjerenja Rockwellove tvrdoće jedne ploče radnici du dobili sljedeće
vrijednosti:
64.9,64.1,63.8,64.0.
Odredite interval povjerenja za očekivanu vrijednost tvrdoće s pouzdanošću 99%.
Rješenje: Za zadanu pouzdanost γ = 0.99 interval povjerenja za očekivanje odrdujemo iz
P(X - λ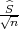 ≤ μ ≤X + λ
≤ μ ≤X + λ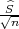 ) = γ.
) = γ.
Za očekivanje μ interval povjerenja pouzdanosti γ je (X-λ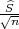 ,X + λ
,X + λ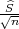 ), gdje je λ =
z
), gdje je λ =
z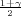 kvantil studentove distribucije t(n - 1).
kvantil studentove distribucije t(n - 1).
Za n = 4, λ = z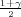 je kvantil studentove distribucije t(3).
je kvantil studentove distribucije t(3).
Iz tablice očitavamo za γ = 0.99, vrijednost λ = z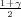 = 5.84.
= 5.84.
Koristeći date vrijednosti iz uzorka x = 64.2, i 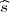 2 = 0.233 dobivamo interval povjerenja
za μ :
2 = 0.233 dobivamo interval povjerenja
za μ :
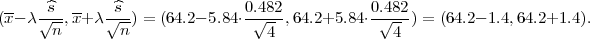 S
pouzdanošću 99% očekivana vrijednost tvrdoće po Rockwellu će se biti u intervalu
[62.8,65.6].
S
pouzdanošću 99% očekivana vrijednost tvrdoće po Rockwellu će se biti u intervalu
[62.8,65.6].
13.4 INTERVAL POVJERENJA ZA VJEROJATNOST BINOMNE
DISTRIBUCIJE
n (n →∞)
MOTIV 13.4
U anketi za izbore dobiveni su podatci za kandidata A:
u uzorku od n=2500 glasača kandidat je dobio 1000 glasova.
Odredite interval povjerenja za postotak glasova koji će dobiti kandidat A na
izborima s pouzdanošću 0.95.
(Pretpostavimo da je izbor binomna distribucija)
U Bernoullijevoj shemi s Xi ~ B(1,p),i = 1,...,n slučajna varijabla
X = ∑
i=1nX
i broj uspjeha u Bernoullijevoj shemi ima binomnu distribuciju
X ~ B(n,p).
Relativna frekvencija uspjeha u Bernoullijevoj shemi je slučajna varijabla 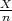 koja
odgovara X =
koja
odgovara X =  ∑
i=1nX
i uzoračkoj aritmetičkoj sredini slučajnog uzorka
(X1,X2,..Xn).
∑
i=1nX
i uzoračkoj aritmetičkoj sredini slučajnog uzorka
(X1,X2,..Xn).
Prisjetimo se da je X = 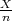 je procjenitelj za vjerojatnost p u Binomnoj distibuciji.
je procjenitelj za vjerojatnost p u Binomnoj distibuciji.
Dokaz: tko želi znati više
Neka je (X1,X2,..Xn) slučajni uzorak iz Bernoullijeve sheme, Xi ~ B(1,p).
Prisjetimo se da vrijedi E(Xi) = p, V ar(Xi) = p(1 - p) i za uzoračku aritmetičku
sredinu X =  ∑
i=1nX
i vrijedi E(X) = p, V ar(X) =
∑
i=1nX
i vrijedi E(X) = p, V ar(X) = 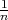 p(1 - p).
p(1 - p).
(a) Prema CGT za (n →∞) za uzoračku aritmetičku sredinu
X =  ∑
i=1nX
i vrijedi X ~ N(p,
∑
i=1nX
i vrijedi X ~ N(p,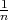 p(1 - p)).
p(1 - p)).
Za simetrični interval (-λ,λ) možemo približno odrediti
P(-λ ≤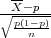 ≤ λ) ≈ 2F*(λ) - 1.
≤ λ) ≈ 2F*(λ) - 1.
Nejednakost -λ ≤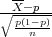 ≤ λ ekvivalentna je nejednakosti: (
≤ λ ekvivalentna je nejednakosti: (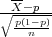 )2 ≤ λ2,
odnosno
)2 ≤ λ2,
odnosno
(n + λ2)p2 - (2Xn + λ2)p + nX2 ≤ 0
Trebamo riješiti nejednakost po p.
Približna rješenja p1,p2 kvadratne jednadžbe (veliko n) su :
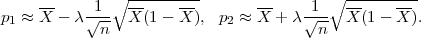
Kako je (n + λ2) > 0, p ∈ (p1,p2).
Zaključujemo da je
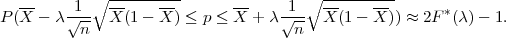
Ako je zadana pouzdanost γ tako da je P(G1 < p < G2) = γ onda možemo odrediti λ
tako da vrijedi F*(λ) = 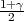 , tj. λ = z
, tj. λ = z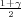 kvantil standardne normalne distibucije
F*(z
kvantil standardne normalne distibucije
F*(z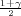 ) =
) = 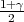 .
.
Procjenitelji G1 = X - λ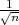
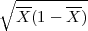 , G2 = X + λ
, G2 = X + λ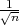
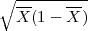 čine
interval povjerenja (G1,G2) za paranetar vjerojatnost p uspjeha u Bernoullijevoj
shemi.
čine
interval povjerenja (G1,G2) za paranetar vjerojatnost p uspjeha u Bernoullijevoj
shemi.
(b) Prema Čebiševljevoj nejednakosti za slučajnu varijablu X koja ima
E(X) = p, V ar(X) = 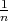 p(1 - p) u obliku
p(1 - p) u obliku
P(p - λ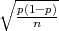 ≤X ≤ p + λ
≤X ≤ p + λ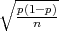 ) ≥ 1 -
) ≥ 1 -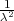 .
.
Nejednakost p-λ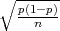 ≤X ≤ p + λ
≤X ≤ p + λ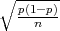 ekvivalentna je nejednakosti (vidi pod
(a)): X - λ
ekvivalentna je nejednakosti (vidi pod
(a)): X - λ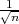
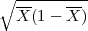 ≤ p ≤X + λ
≤ p ≤X + λ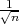
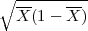 .
.
Zaključujemo da je
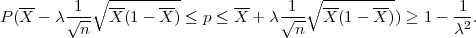
Ako je zadana pouzdanost γ tako da je P(G1 < p < G2) = γ onda možemo odrediti λ
tako da vrijedi 1 -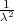 = γ tj. λ =
= γ tj. λ = 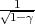 .
.
Procjenitelji G1 = X - λ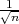
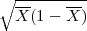 , G2 = X + λ
, G2 = X + λ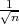
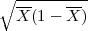 čine
interval povjerenja (G1,G2) za paranetar vjrojatnosti p uspjeha u Bernoullijevoj
shemi.
čine
interval povjerenja (G1,G2) za paranetar vjrojatnosti p uspjeha u Bernoullijevoj
shemi.
NAPOMENA 13.7 Možemo izvesti interval povjerenja i koristeći teorem
Moivre-Laplacea (CGT) za relativnu frekvenciju u Bernullijevoj shemi
P(|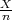 - p| < ε) ≈ F*(ε
- p| < ε) ≈ F*(ε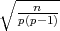 ) - 1, n →∞,
) - 1, n →∞,
tj.
P(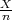 - ε < p <
- ε < p < 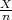 + ε) ≈ F*(ε
+ ε) ≈ F*(ε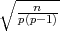 ) - 1.
) - 1.
Ako je zadana pozdanost γ, P(G1 < p < G2) = γ, onda možemo odrediti ε tako
da vrijedi F*(ε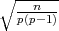 ) =
) = 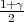 , tj. ε = z
, tj. ε = z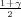
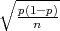 , odnosno ε = z
, odnosno ε = z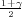
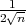 , uz
p(1 - p) ≤
, uz
p(1 - p) ≤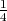 .
.
Procjenitelji G1 = 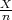 - ε, G2 =
- ε, G2 = 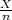 - ε čine interval povjerenja (G1,G2) za
paranetar vjerojatnosti p uspjeha u Bernoullijevoj shemi. varijable
- ε čine interval povjerenja (G1,G2) za
paranetar vjerojatnosti p uspjeha u Bernoullijevoj shemi. varijable
X ~ B(n,p) s pouzdanošću γ ako je poznat parametar n broj ponavljanja pokusa.
Parametar vjerojatnost p s pozdanošću γ poprimit će vrijednosti u u intervalu
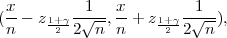
gdje je z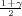 kvantil standardne normalne distribucije F*(z
kvantil standardne normalne distribucije F*(z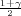 ) =
) = 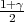 .
.
PRIMJER 13.6 Odredite interval povjerenja za vjerojatnost p u Bernoullijevoj
shemi s pouzdanošću γ = 0.95 ako se pokus ponovi n=100, a broj uspjeha je 32.
Rješenje: Za slučajnu varijablu X ~ B(n,p) vrijedi
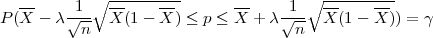
gdje je λ = z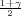 kvantil standardne normalne distibucije F*(z
kvantil standardne normalne distibucije F*(z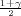 ) =
) = 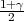 , X =
, X = 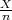 relativna frekvencija uspjeha.
relativna frekvencija uspjeha.
Procjenitelji G1 = X - λ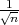
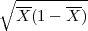 , G2 = X + λ
, G2 = X + λ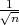
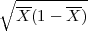 čine interval
povjerenja (G1,G2) za paranetar vjerojatnosti p.
čine interval
povjerenja (G1,G2) za paranetar vjerojatnosti p.
Parametar vjerojatnost p s pouzdanošću γ poprimit će vrijednosti u intervalu
(x-λ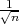
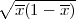 ,x + λ
,x + λ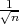
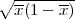 ) gdje je λ = z
) gdje je λ = z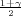 kvantil standardne normalne
distibucije.
kvantil standardne normalne
distibucije.
Iz uzorka je uzeta relativna fekvencija x = 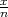 =
= 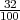 , za pouzdanost γ = 0.95 iz tablice
očitamo λ = z
, za pouzdanost γ = 0.95 iz tablice
očitamo λ = z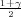 = 1.96 i odredimo interval
= 1.96 i odredimo interval
Parametar vjerojatnosti p s pouzdanošću γ = 0.95 poprimit će vrijednosti u intervalu
(0.23,0.41).
PRIMJER 13.7 Pravljena je anketa o dolasku na predavanja VIS. Na uzorku
163 studenta njih 62 je odgovorilo da je dolazilo na predavanja. Odredite interval
povjerenja za vjerojatnost dolaska studenata prve godine na predavanja VIS s
pouzdanošću 0.95.
(Pretpostavimo da je izbor binomna distribucija)
Rješenje: Parametar vjerojatnosti p s pozdanošću γ poprimit će vrijednosti u u
intervalu (x-λ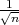
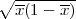 ,x + λ
,x + λ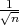
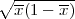 ) gdje je λ = z
) gdje je λ = z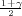 kvantil standardne
normalne distibucije.
kvantil standardne
normalne distibucije.
Iz uzorka je uzeta relativna fekvencija x = 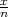 =
= 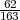 = 0.38, za pouzdanost
= 0.38, za pouzdanost
γ = 0.95 iz tablice očitamo λ = z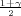 = 1.96 i odredimo interval
= 1.96 i odredimo interval
Parametar vjerojatnosti p s pouzdanošću γ = 0.95 poprimit će vrijednosti u intervalu
(0.30,0.45).
Vjerojatnost dolaska na predavanja VIS s pouzdanošću 0.95 je izmedu 0.30 i
0.45.
PRIMJER 13.8 motiv
U anketi za izbore dobiveni su podatci za kandidata A:
u uzorku od n=2500 glasača kandidat je dobio 1000 glasova.
Odredite interval povjerenja za postotak glasova koji će dobiti kandidat A na
izborima s pouzdanošću 0.95.
(Pretpostavimo da je izbor binomna distribucija)
Rjšenje: Parametar vjerojatnost p s pozdanošću γ poprimit će vrijednosti u u
intervalu (x-λ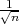
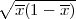 ,x + λ
,x + λ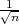
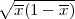 ) gdje je λ = z
) gdje je λ = z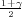 kvantil standardne
normalne distibucije.
kvantil standardne
normalne distibucije.
Iz uzorka imamo relativnu fekvenciju x = 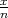 =
= 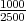 = 0.4, za pouzdanost γ = 0.95 iz
tablice očitamo λ = z
= 0.4, za pouzdanost γ = 0.95 iz
tablice očitamo λ = z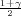 = 1.96 i odredimo interval
= 1.96 i odredimo interval
Parametar vjerojatnosti p s pozdanošću γ = 0.95 poprimit će vrijednosti u intervalu
(0.38,0.42).
Postotak glasova koje će na izborima dobiti kandidat A s pouzdanošću 0.95 je izmedu
38% i 42%.
PRIMJER 13.9 Ako želimo odrediti postotak p% glasova koje će dobiti kandidat
A na izborima pravimo anketu. Koliki uzorak treba uzeti da bi se za p odredio
interval pouzdanosti 0.95 širine 0.04?
Rješenje: Parametar vjerojatnost p s pozdanošću γ poprimit će vrijednosti u u
intervalu (x-λ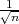
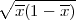 ,x + λ
,x + λ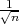
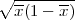 ) gdje je λ = z
) gdje je λ = z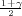 kvantil standardne
normalne distibucije.
kvantil standardne
normalne distibucije.
Širina intervala δ = 2λ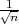
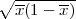 .
.
Kako je x(1 -x) ≤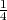 možemo ocijeniti veličinu uzorka n: n ≤
možemo ocijeniti veličinu uzorka n: n ≤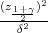 .
.
Za zadane δ = 0.04, γ = 0.95, dobivamo λ = z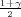 = 1.96 i
= 1.96 i
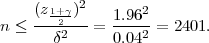
Uzorak mora imati bar 2401 glasača da bi s pouzdanošću 0.95 interval povjerenja za
postotak bodova na izborima za kandidata A bio širok 0.04. (greška unutar
4%).
13.5 Ponovimo
INTERVAL POVJERENJA ZA parametar t
|
|
| slučajni uzorak | (X1,X2,...,Xn) |
|
|
| parametar | t |
|
|
| pouzdanost | γ |
|
|
| interval povjerenja za t | P(G1 ≤ t ≤ G2) ≥ γ |
|
|
| |
INTERVAL POVJERENJA ZA OČEKIVANJE kad je n →∞
|
|
| slučajni uzorak | (X1,X2,...,Xn), n ≥ 30 |
|
|
| parametar | μ |
|
|
| pouzdanost | γ |
|
|
| interval povjerenja za t | P(G1 ≤ μ ≤ G2) ≥ γ |
|
|
| | G1 = X - λ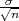 |
|
|
| | G2 = X + λ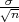 |
|
|
| λ | z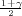 , kvantil N(0,1) , kvantil N(0,1) |
|
|
| |
INTERVAL POVJERENJA ZA OČEKIVANJE NORMALNE distribucije
(varijanca poznata)
|
|
| slučajni uzorak | (X1,X2,...,Xn), iz N(μ,σ2) |
|
|
| parametar | μ |
|
|
| pouzdanost | γ |
|
|
| interval povjerenja za μ | P(G1 ≤ μ ≤ G2) ≥ γ |
|
|
| | G1 = X - λ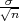 |
|
|
| | G2 = X + λ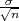 |
|
|
| λ | z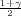 , kvantil N(0,1) , kvantil N(0,1) |
|
|
| |
INTERVAL POVJERENJA ZA OČEKIVANJE NORMALNE distribucije
(varijanca nepoznata)
|
|
| slučajni uzorak | (X1,X2,...,Xn), iz N(μ,σ2) |
|
|
| parametar | μ |
|
|
| pouzdanost | γ |
|
|
| interval povjerenja za μ | P(G1 ≤ μ ≤ G2) ≥ γ |
|
|
| | G1 = X - λ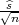 |
|
|
| | G2 = X + λ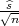 |
|
|
| λ | z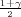 , kvantil t(n - 1) , kvantil t(n - 1) |
|
|
| |
INTERVAL POVJERENJA ZA VJEROJATNOST BINOMNE distribucije
(veliki n)
|
|
| slučajni uzorak | (X1,X2,...,Xn), iz B(n,p) |
|
|
| parametar | p |
|
|
| pouzdanost | γ |
|
|
| interval povjerenja za μ | P(G1 ≤ p ≤ G2) ≥ γ |
|
|
| | G1 = 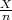 - λ - λ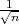 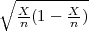 |
|
|
| | G2 = 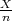 + λ + λ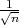 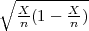 |
|
|
| λ | z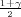 , kvantil N(0,1) , kvantil N(0,1) |
|
|
| |
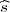 2).
2).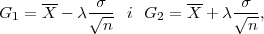
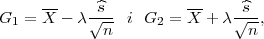
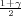 kvantil standardne normalne
distribucije F*(z
kvantil standardne normalne
distribucije F*(z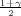 ) =
) = 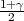 .
.