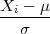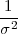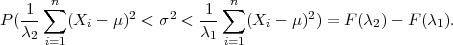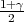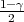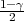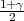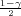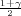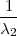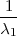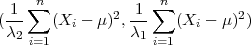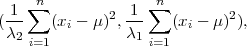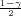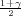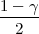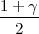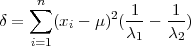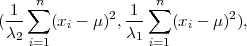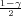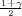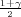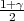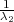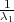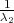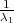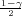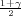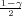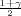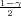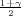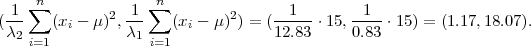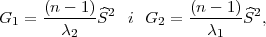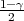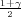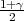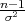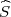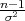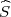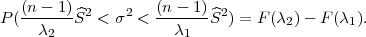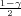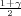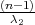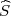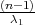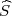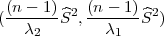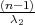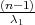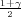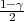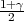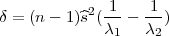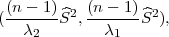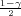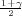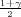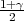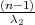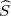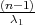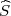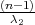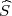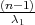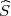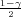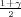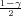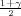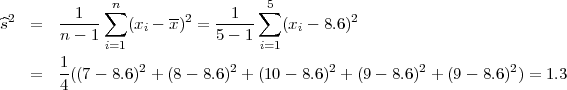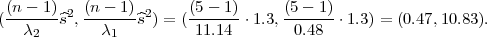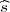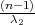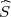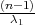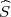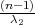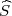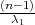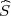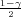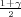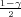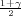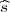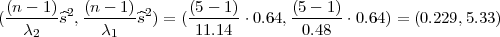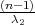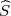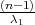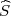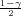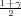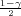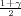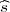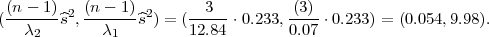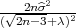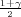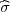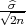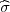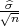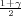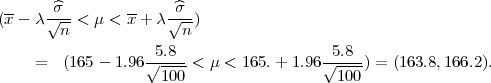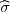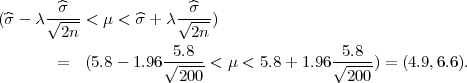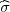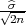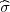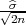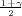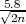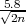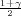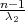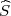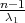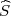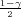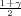Poglavlje 14
INTERVAL POVJERENJA ZA VARIJANCU
14.1 INTERVAL POVJERENJA ZA VARIJANCU NORMALNU distribucije
poznatog očekivanja
MOTIV 14.1
Neka slučajna varijabla ima normalnu distribuciju
X ~ N(μ,σ2) nepoznate varijance σ2 i poznatog očekivanja μ = 10. Uzet je uzorak
veličine n = 5 i dobivena je vrijednost uzorka (7,8,10,9,9). Odredite interval
povjerenja za varijancu σ2 slučajne varijable s pouzdanošću γ = 0.95.
Dokaz: tko želi znati više
Neka je X ~ N(μ,σ2) , onda je Y = ∑
i=1n(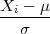 )2 ~ χ2(n).
)2 ~ χ2(n).
Na intervalu (λ1,λ2) :
P(λ1 < 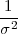 ∑
i=1n(X
i - μ)2 < λ
2) = F(λ2) - F(λ1), tj.
∑
i=1n(X
i - μ)2 < λ
2) = F(λ2) - F(λ1), tj.
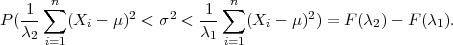
Ako je zadana pozdanost γ, P(G1 < σ2 < G2) = γ = 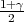 -
-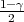 , onda možemo odrediti
λ1,λ2 tako da vrijedi F(λ1) =
, onda možemo odrediti
λ1,λ2 tako da vrijedi F(λ1) = 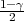 ,F(λ2) =
,F(λ2) = 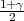 tj. λ1 = z
tj. λ1 = z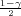 , λ2 = z
, λ2 = z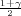 su kvantili
hikvadrat distribucije χ2(n).
su kvantili
hikvadrat distribucije χ2(n).
Procjenitelji G1 = 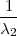 ∑
i=1n(X
i - μ)2, G
2 =
∑
i=1n(X
i - μ)2, G
2 = 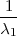 ∑
i=1n(X
i - μ)2 čine interval
povjerenja
∑
i=1n(X
i - μ)2 čine interval
povjerenja
za parametar σ2 slučajne varijable X ~ N(μ,σ2) s pouzdanošću γ.
Parametar varijanca σ2 s pouzdanošću γ poprimit će vrijednosti u intervalu
gdje su λ1 = z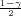 , λ2 = z
, λ2 = z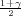 kvantili hikvadrat distribucije χ2(n).
kvantili hikvadrat distribucije χ2(n).
Ako je tablica hikvadrat distribucije Y ~ χ2(n), dana u obliku
P(Y > ε) = p, onda P(Y > λ2) = 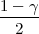 , P(Y > λ1) =
, P(Y > λ1) = 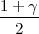 .
.
NAPOMENA 14.1 Ova procjena parametra varijance slučajne varijable
X ~ N(μ,σ2) poznatog očekivanja može koristiti za odredivanje širine inervala
uz zadanu pozdanost γ za interval povjerenja
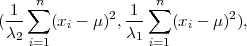
gdje su λ1 = z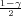 , λ2 = z
, λ2 = z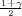 kvantili hikvadrat distribucije χ2(n - 1).
kvantili hikvadrat distribucije χ2(n - 1).
PRIMJER 14.1 motiv
Neka slučajna varijabla ima normalnu distribuciju
X ~ N(μ,σ2) nepoznate varijance σ2 i poznatog očekivanja μ = 10. Uzet je uzorak
veličine n = 5 i dobivena je vrijednost uzorka (7,8,10,9,9). Odredite interval
povjerenja za varijancu σ2 slučajne varijable s pouzdanošću γ = 0.95.
Rješenje: P(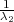 ∑
i=1n(xi - μ)2 < σ2 <
∑
i=1n(xi - μ)2 < σ2 < 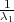 ∑
i=1n(xi - μ)2) = γ.
∑
i=1n(xi - μ)2) = γ.
Za varijancu σ2, poznatog očekivvanja interval povjerenja pouzdanosti γ je
(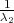 ∑
i=1n(xi - μ)2,
∑
i=1n(xi - μ)2,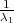 ∑
i=1n(xi - μ)2), gdje su λ1 = z
∑
i=1n(xi - μ)2), gdje su λ1 = z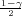 , λ2 = z
, λ2 = z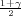 kvantili
hikvadrat distribucije χ2(n).
kvantili
hikvadrat distribucije χ2(n).
Za n = 5, λ1 = z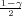 , λ2 = z
, λ2 = z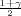 .
.
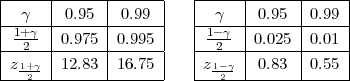
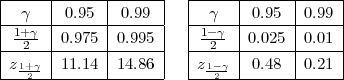
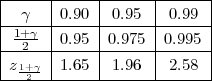
Iz tablice očitavamo za γ = 0.95, λ1 = z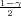 = 0.83,λ2 = z
= 0.83,λ2 = z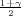 = 12.83.
= 12.83.
Koristeći date vrijednosti iz uzorka ∑
i=15(x
i - 10)2 = 32 + 22 + 12 + 12 = 15
dobivamo interval povjerenja za σ2 :
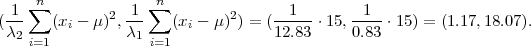
14.2 INTERVAL POVJERENJA ZA VARIJANCU NORMALNE distribucije
nepoznatog očekivanja
MOTIV 14.2
U četiri mjerenja Rockwellove tvrdoće jedne ploče radnici du dobili sljedeće
vrijednosti:
64.9,64.1,63.8,64.0.
Odredite interval povjerenja za varijancu tvrdoće s pouzdanošću 99%.
TEOREM 14.2 Neka je (X1,X2,..Xn) slučajni uzorak slučajne varijable
X ~ N(μ,σ2) s nepoznatim parametrom varijancom σ2, nepoznatog očekivanja μ.
Interval povjerenja (G1,G2) za varijance σ2 s pouzdanošću γ čine procjenitelji:
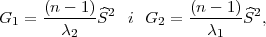
gdje je 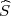 2 korigirana uzoračka varijanca, a λ1 = z
2 korigirana uzoračka varijanca, a λ1 = z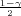 , λ2 = z
, λ2 = z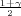 , kvantili
hikvadrat distribucije χ2(n - 1),
, kvantili
hikvadrat distribucije χ2(n - 1),
F(z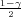 ) =
) = 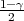 , F(z
, F(z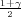 ) =
) = 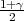 .
.
Dokaz: tko želi znati še
Neka je X ~ N(μ,σ2), onda je Y = 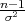
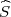 2 ~ χ2(n - 1).
2 ~ χ2(n - 1).
Na intervalu (λ1,λ2) : P(λ1 < 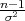
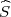 2 < λ2) = F(λ2) - F(λ1) tj.
2 < λ2) = F(λ2) - F(λ1) tj.
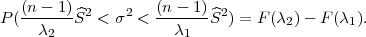
Ako je zadana pozdanost γ, P(G1 < σ2 < G2) = γ = 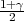 -
-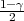 , i onda možemo
odrediti λ1,λ2 tako da vrijedi F(λ1) =
, i onda možemo
odrediti λ1,λ2 tako da vrijedi F(λ1) = 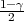 ,F(λ2) =
,F(λ2) = 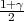 tj. λ1 = z
tj. λ1 = z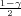 , λ2 = z
, λ2 = z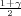 kvantili hikvadrat distribucije χ2(n - 1).
kvantili hikvadrat distribucije χ2(n - 1).
Procjenitelji G1 = 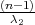
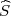 2, G2 =
2, G2 = 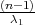
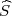 2 čine interval povjerenja
2 čine interval povjerenja
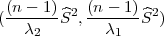
za parametar σ2 slučajne varijable X ~ N(μ,σ2) s pouzdanošću γ.
Parametar varijanca σ2 s pouzdanošću γ poprimit će vrijednosti u u intervalu
(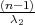
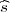 2,
2,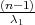
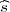 2), gdje su λ1 = z
2), gdje su λ1 = z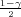 , λ2 = z
, λ2 = z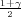 kvantili hikvadrat distribucije
χ2(n - 1).
kvantili hikvadrat distribucije
χ2(n - 1).
Ako je tablica hikvadrat distribucije Y ~ χ2(n - 1), dana u obliku
P(Y > ε) = p, onda P(Y > λ2) = 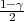 , P(Y > λ1) =
, P(Y > λ1) = 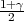 .
.
NAPOMENA 14.3 Ova procjena parametra varijance slučajne varijable
X ~ N(μ,σ2) nepoznatog očekivanja može koristiti za odredivanje
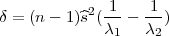
širine inervala uz zadanu pozdanost γ za interval povjerenja
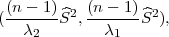
gdje su λ1 = z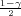 , λ2 = z
, λ2 = z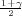 kvantili hikvadrat distribucije χ2(n - 1).
kvantili hikvadrat distribucije χ2(n - 1).
PRIMJER 14.2 Neka slučajna varijabla ima normalnu distribuciju
X ~ N(μ,σ2) nepoznate varijance σ2 i nepoznatog očekivanja μ. Uzet je uzorak
veličine n = 5 i dobivena je vrijednost uzorka (7,8,10,9,9). Odredite interval
povjerenja za varijancu σ2 slučajne varijable s pouzdanošću γ = 0.95.
Rješenje: P(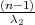
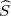 2 < σ2 <
2 < σ2 < 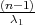
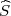 2) = γ.
2) = γ.
Za varijancu σ2 interval povjerenja pouzdanosti γ je (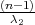
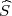 2,
2,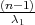
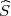 2), gdje su
λ1 = z
2), gdje su
λ1 = z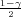 , λ2 = z
, λ2 = z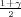 kvantili hikvadrat distribucije χ2(n - 1).
kvantili hikvadrat distribucije χ2(n - 1).
Za n = 5, iz tablice očitavamo za γ = 0.95, λ1 = z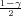 = 0.48,
= 0.48,
λ2 = z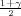 = 11.14.
= 11.14.
Koristeći date vrijednosti iz uzorka: x = 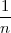 ∑
i=1nx
i =
∑
i=1nx
i =  (7 + 8 + 10 + 9 + 9) = 8.6,
(7 + 8 + 10 + 9 + 9) = 8.6,
∑
i=15(x
i -x)2 = 32 + 22 + 12 + 12 = 15
dobivamo interval povjerenja za σ2 :
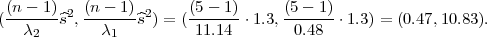
PRIMJER 14.3 Neka slučajna varijabla ima normalnu distribuciju
X ~ N(μ,σ2) nepoznate varijance σ2 i nepoznatog očekivanja μ. Uzet je uzorak
veličine n = 5 i dobivena je vrijednost korigirane uzoračke varijance 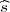 2 = 0.64.
Odredite interval povjerenja za varijancu σ2 slučajne varijable s pouzdanošću
γ = 0.95.
2 = 0.64.
Odredite interval povjerenja za varijancu σ2 slučajne varijable s pouzdanošću
γ = 0.95.
Rješenje: P(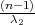
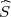 2 < σ2 <
2 < σ2 < 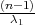
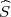 2) = γ.
2) = γ.
Za varijancu σ2 interval povjerenja pouzdanosti γ je (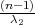
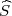 2,
2,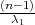
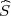 2), gdje su
λ1 = z
2), gdje su
λ1 = z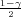 , λ2 = z
, λ2 = z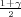 kvantili hikvadrat distribucije χ2(n - 1).
kvantili hikvadrat distribucije χ2(n - 1).
Za n = 5, iz tablice očitavamo za γ = 0.95, λ1 = z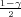 = 0.48,
= 0.48,
λ2 = z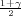 = 11.14.
= 11.14.
Koristeći date vrijednosti iz uzorka 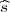 2 = 0.64 dobivamo interval povjerenja za
σ2 :
2 = 0.64 dobivamo interval povjerenja za
σ2 :
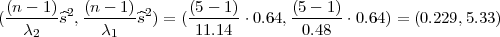
PRIMJER 14.4 motiv
U četiri mjerenja Rockwellove tvrdoće jedne ploče radnici du dobili sljedeće
vrijednosti:
64.9,64.1,63.8,64.0.
Odredite interval povjerenja za varijancu tvrdoće s pouzdanošću 99%.
Rješenje:
Za varijancu σ2 interval povjerenja pouzdanosti γ je (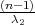
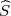 2,
2,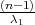
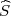 2), gdje su
λ1 = z
2), gdje su
λ1 = z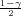 , λ2 = z
, λ2 = z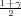 kvantili hikvadrat distribucije χ2(n - 1).
kvantili hikvadrat distribucije χ2(n - 1).
Za n = 4, i γ = 0.99, iz tablice za χ2(3) očitavamo za λ1 = z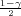 = 0.07
= 0.07
λ2 = z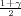 = 12.84.
= 12.84.
Koristeći date vrijednosti iz uzorka 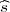 2 = 0.233 dobivamo interval povjerenja za
σ2 :
2 = 0.233 dobivamo interval povjerenja za
σ2 :
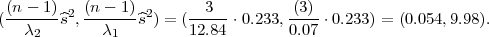 Interval povjerenja za varijancu uz pouzdanost 99% je [0.05,9.98].
Interval povjerenja za varijancu uz pouzdanost 99% je [0.05,9.98].
PRIMJER 14.5 Uzet je uzorak veličine 100 za visinu 18-godišnjakinja i
dobivene su vrijednosti za uzoračku aritmetičku sredinu x = 165 cm i uzoračku
varijancu 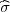 2 = 5.82 cm.
2 = 5.82 cm.
Pretpostavimo da visina djevojaka ima normalnu distribuciju.
(a) Odredite interval povjerenja za očekivnje μ (srednju visinu) s pouzdanošću
γ = 0.95.
(b) Odredite interval povjerenja za standardnu devijaciju σ s pouzdanošću
γ = 0.95.
(c) Koliki treba biti uzorak da s pouzdanošću γ = 0.95 standardna devijacija
ne odstupa od uzoračke standardne devijacije više od 5%?
Rješenje:
(a) za n > 30, P(X - λ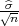 < μ < X + λ
< μ < X + λ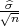 ) = γ, λ = z
) = γ, λ = z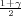 kvantili standardne
kvantili standardne
normalne distribucije
(b) za n ≥ 100, P(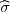 - λ
- λ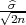 < σ <
< σ < 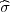 + λ
+ λ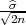 ) = γ, λ = z
) = γ, λ = z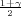 kvantili
kvantili
standardne normalne distribucije
(c) P(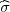 - λ
- λ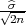 < σ <
< σ < 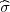 + λ
+ λ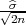 ) = γ, λ = z
) = γ, λ = z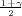 kvantili standardne normalne
distribucije.
kvantili standardne normalne
distribucije.
Iz P(5.8 - 1.96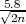 < σ < 5.8 + 1.96
< σ < 5.8 + 1.96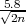 ) = 0.95 i uvjeta 1.96
) = 0.95 i uvjeta 1.96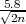 < 5.8 ⋅ 5%
< 5.8 ⋅ 5%
zaključujemo da je za n ≥ 769.
14.3 Ponovimo
INTERVAL POVJERENJA ZA VARIJANCU NORMALNE distribucije
(očekivanje poznato)
|
|
| slučajni uzorak | (X1,X2,...,Xn), iz N(μ,σ2) |
|
|
| parametar | σ2 |
|
|
| pouzdanost | γ |
|
|
| interval povjerenja za σ2 | P(G1 ≤ σ2 ≤ G2) ≥ γ |
|
|
| | G1 = 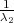 ∑
i=1n(Xi - μ)2 ∑
i=1n(Xi - μ)2 |
|
|
| | G1 = 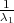 ∑
i=1n(Xi - μ)2 ∑
i=1n(Xi - μ)2 |
|
|
| λ1 | z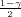 , kvantil χ2(n) , kvantil χ2(n) |
|
|
| λ2 | z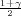 , kvantil χ2(n) , kvantil χ2(n) |
|
|
| |
INTERVAL POVJERENJA ZA VARIJANCU NORMALNE distribucije
(očekivanje nepoznato)
|
|
| slučajni uzorak | (X1,X2,...,Xn), iz N(μ,σ2) |
|
|
| parametar | σ2 |
|
|
| pouzdanost | γ |
|
|
| interval povjerenja za σ2 | P(G1 ≤ σ2 ≤ G2) ≥ γ |
|
|
| | G1 = 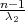 ⋅ ⋅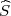 2 2 |
|
|
| | G2 = 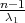 ⋅ ⋅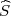 2 2 |
|
|
| λ1 | z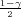 , kvantil χ2(n - 1) , kvantil χ2(n - 1) |
|
|
| λ2 | z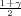 , kvantil χ2(n - 1) , kvantil χ2(n - 1) |
|
|
| |
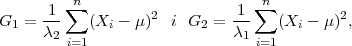
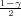 , λ2 = z
, λ2 = z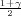 , kvantili hi-kvadrat distribucije χ2(n),
, kvantili hi-kvadrat distribucije χ2(n),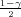 ) =
) = 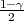 , F(z
, F(z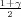 ) =
) = 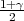 .
.